
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Начальные параметры в обобщенном уравнении изогнутой оси балки, их определение.Содержание книги
Поиск на нашем сайте Если сразу известны нач. параметры
Начальный угол поворота не равен нулю. Начальный прогиб = 0.
Если левый конец балки свободен, то оба нач. параметра не равны нулю.
Метод непосредственного интегрирования и метод начальных параметров применяется для балок постоянного поперечного сечения.
6. Энергетический метод определения перемещений.
Работа произвольной сис-мы сил равна:
При применении энергетич. Метода как линейные, так и угловые перемещения обозначают Δ. Для определения работы внутренней силы, численно равной потенциальной энергии деформации, выделим из балки, находящейся в условиях чистого изгиба бесконечно малый элемент dz.
Это выражение даёт величину потенциальной энергии для элемента балки, находящегося в условиях чистого изгиба. При поперечном изгибе, когда кроме изгибающего момента, возникают и поперечные силы,ф-ла для вычисления энергии будет иметь вид: dU= Коэффициент К зависит от размеров сечения и в какой-то мере учитывает неравномерность распределения касат.напр-й по сечению. При вычислении энергии деф-ции изгиба поперечными силами Q можно пренебречь, т.к. последнее слагаемое составляет 2-3% от всей энергии деф-ции. Для вычисления энергии деф-ции балки в целом следует просуммировать значение dU по всей её длине. Окончательная ф-ла для определения энергии деф-ции при изгибе имеет вид:
7. Универсальный метод определения перемещений (интеграл Мора). Пусть требуется определить прогиб в точке 1 двухопорной балки. Для упрощения вывода показываем только одну силу, но формула, которая будет получена, справедлива для любых нагрузок. Рисунок:
Если требуется определить перемещение в точке 1 под действием силы F2, приложенной к точке 2. Делают следующее: В точке 1 прикладывают силу F1=1, балка прогибается. Точка 1 перемещается на ∆11 (1-индекс указывает точку, в которой определяется перемещение, 2-индекс указывает точку, где приложена сила). Сила F1 постепенно нарастая, совершает на этом перемещении работу: W1= Накопленная балкой энергия в этом случае равна: U1= ∑ ∫ (M12 dz ∕ 2EIx) = W1. Точка 2 перемещается в новое положение, но поскольку она свободна от нагрузок, то изменение энергии в балке не происходит. К новому положению точки 2 прикладываем силу F2, точка 2 дополнительно перемещается на ∆22 и сила F2, постепенно нарастая, совершает работу: W2= Дополнительная потенциальная энергия будет равна: U2= ∑ ∫ (M22 dz ∕ 2EIx)= W2. Под действием силы F2, точка 1 дополнительно перемещается на ∆12, а сила F1 оставаясь постоянной, совершает на этом перемещении работу W12 =F1∙∆12 – это возможная или виртуальная работа, т.е. работа на чужом перемещении. Суммарная работа: W=W1+W2+W12= Суммарная потенциальная энергия равна: U= Т.к. U=W, получим: F1∙∆12= В общем случае, когда определяют перемещение в любой точке от действия на балку группы сил F, то выражение примет вид: ∆1F = M1- изгибающие моменты в сечениях балки от единичной силы. MF – изгибающие моменты от заданной нагрузки.
8. Порядок определения перемещение с помощью интеграла Мора. 1) Составляется уравнение изгибающих моментов от нагрузки MF. 2) Освободив балку от нагрузки, прикладываем к ней единичную силу в той точке, где хотим определить перемещение по направлению этого перемещения. 3) Составляется уравнение изгибающих моментов от единичной силы F1. 4) Полученные выражения моментов подставляются в интеграл Мора, и производится интегрирование и суммирование по длине системы. Если в результате интегрирования и суммирования получают знак «+», то перемещение произошло по направлению единичной силы. Если определению подлежит не прогиб, а угол поворота сечения, то к разгруженной балке следует приложить в этом сечении единичный момент.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 566; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 можно сразу найти прогиб и угол попорота в любом сечении балки, но они не всегда известны. Нач. параметры опр-ся из граничных условий. Рассм. 1-ый и запишем:
можно сразу найти прогиб и угол попорота в любом сечении балки, но они не всегда известны. Нач. параметры опр-ся из граничных условий. Рассм. 1-ый и запишем: z=0;
z=0; 
 z=0;
z=0; 
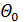 Находится из условия, что прогиб на 2-ой опоре = 0.
Находится из условия, что прогиб на 2-ой опоре = 0. при z=0;
при z=0; 

 – теорема Клайперона
– теорема Клайперона


 ; dΘ=
; dΘ= 






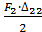
 + F1∙∆12
+ F1∙∆12
 . Сила F1=1, поэтому ∆12=
. Сила F1=1, поэтому ∆12=  - формула Мора.
- формула Мора.


