
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пределы применимости формулы ЭйлераСодержание книги Поиск на нашем сайте Формула Эйлера применима при работе трения в упругой стадии, когда критическое напряжение меньше предела пропорциональности формула. Теперь можно получить предельную гибкость при которой и больше которой можно пользоваться ф-лой Эйлера. δкр=π^2*E\λ^2 В дальнейшем стержни по гибкости будем разделять на 3 группы: 1.Стержень большой гибкости λ>λ0=100 δкр<δпр Такие стержни рассчитываются на устойчивость по формуле Эйлера. Fкр=π^2EImin\μl^2 2. Стержень средней гибкости. рассчитывается на прочность и устойчивость λ=60:100 δр<δкр<δу Для таких стержней применяется напряжение определяющееся по формуле Яшинского. δпр=авλ а и в постоянные для материала. Для стали а=310МПА, в=1,41МПА Fкр=δпр*А 3. Стержень малой гибкости Λ=0:60 Рассчитывается только на прочность δкр=δу δ=F\A≤R Можно построить график продольных напряжений для стали
РАСЧЕТ НА УСТОЙЧИВОСТЬ Поскольку стержни рассчитывающиеся на устойчивость находятся под действием сжимающейся силы, условия прочности и условия устойчивости записываются аналогично. Условия прочности на сжатие: δ=F\A≤R R=δ0\K Опасное напряжение для пластичных напряжений равно пределу текучести δ0=δy. Для хрупких материалов опасное напряжение равно пределу прочности Условие устойчивости δ=F\A≤Ry Ry=δy\Ky Коэффициент (фи) зависит от гибкости стержня и определяется по таблице по λ и материалу стержня. Условие устойчивости имеет вид: δ=F\A≤Ry При расчете на прочность учитывается ослабленное сечение.
30. ПРОВЕРОЧНЫЙ И ПРОЕКТИРОВОЧНЫЙ РАСЧЕТЫ НА УСТОЙЧИВОСТЬ При проверочном расчете, когда площадь поперечного сечения задана, проверяют условие устойчивости след. образом: 1)определяют минимальный радиус инерции imin = 2)определяют гибкость стойки ʎ= 3)по гибкости и материалу стержня определяют коэф-т φ; ʎ → φ 3) imin = 7) сравниваем
31. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ
Изгибающий момент в сечении на расстоянии z можно рассматривать как сумму двух моментов. М= - (Мо+ Nу) , где Мо- изгибающий момент от поперечных нагрузок,
Решение этого уравнения представляет собой сумму 2 интегралов: интегр. однородного уравнения и частного интеграла неоднород. уравнения. Такая задача имеет сложное решение. Поэтому использ. приближ. метод решения т.е. задается деформация балки или стойки,но таким образом чтобы удовлетвор-сь граничные условия. при z= здесь µ=1 Fэ= ymax -Nymax =Мо σmax= [ №18 Jx=1090 см4 ; ix=7,24 см; Wx=121 cм3 ; A=20,7 см; Е=210 Гпа; R=200Мпа ymax= yo = ymax =
σmax =109,4Мпа <R
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1106; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |




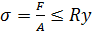
 ; A ≥
; A ≥ 
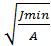 4) ʎ=
4) ʎ= 
 и R. Если расхождение не превышает 5%,то расчет заканчивается,в противном случае задается новое значение
и R. Если расхождение не превышает 5%,то расчет заканчивается,в противном случае задается новое значение  .
.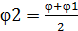 , и далее расчет повторяется.
, и далее расчет повторяется.

 y= -
y= - 
 z; Проверим выполнение граничных условий.
z; Проверим выполнение граничных условий.
 sin
sin 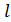 /2 y= EJ ymax
/2 y= EJ ymax  =Fэ – Эйлерова сила
=Fэ – Эйлерова сила ymax=
ymax=  ymax-полный прогиб от совместного действия поперечных и продольных сил.
ymax-полный прогиб от совместного действия поперечных и продольных сил. +
+ 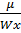 =
= 
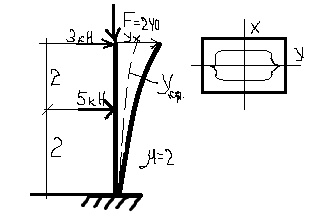
 ; Fэ=
; Fэ= 

 =
=  Fэ=705 кН
Fэ=705 кН Проверим прочность σmax= 181Мпа
Проверим прочность σmax= 181Мпа 

 =110
=110



