
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о циркуляции вектора магнитной индукции в вакуумеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Циркуляцией вектора
Теорема о циркуляции вектора
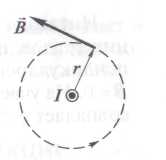
n– число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Например, для системы токов, изображенных на рисунке
Пример: применяя теорему о циркуляции, рассчитаем магнитное поле прямого тока J, перпендикулярного плоскости чертежа и направленного к нам. Замкнутый контур выбираем в виде окружности радиуса r. В каждой точке этого контура вектор Следовательно, циркуляция вектора
Согласно теореме о циркуляции
Откуда магнитная индукция
Сравнивая выражения Видим, что между ними существует принципиальное отличие. Циркуляция вектора Поток вектора магнитной индукции Теорема Гаусса для вектора магнитной индукции По аналогии с потоком вектора
- скалярная величина, где Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору
Единица магнитного потока - вебер (Вб); 1Вб = 1Тл*м2. Магнитный поток характеризует магнитное поле, пронизывающее поверхность. Теорема Гаусса для поля
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. Работа по перемещению проводника с током в магнитном поле
Контур с током (неподвижный проводник и скользящая по нему перемычка длиной l) помещен во внешнее однородное магнитное поле, перпендикулярное плоскости контура. На перемычку (проводник с током) в магнитном поле действует сила Ампера, и перемычка будет перемещаться. Следовательно, магнитное поле совершает работу по перемещению проводника с током. Сила, направление которой определяется по правилу левой руки, а значение по закону Ампера, равна
Работа, совершаемая магнитным полем, из положения 1 в положение 2, равна
Где
т.е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Работа по перемещению в магнитном поле замкнутого контура с постоянным током из начального положения 1 в конечное положение 2
где Теорема о циркуляции вектора напряженности магнитного поля Аналогом вектора электрического смещения D является вектор напряженности Н магнитного поля. В случае вакуума
Единица напряженности магнитного поля – 1 А/м – напряженность такого поля, магнитная индукция которого в вакууме равна
где
где Тогда
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 1514; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

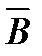 (по аналогии с циркуляцией вектора напряженности электрического поля) по замкнутому контуру называют интеграл
(по аналогии с циркуляцией вектора напряженности электрического поля) по замкнутому контуру называют интеграл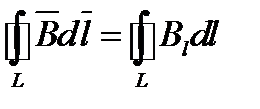 где
где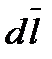 - вектор элементарной длины контура, направленной вдоль обхода контура;
- вектор элементарной длины контура, направленной вдоль обхода контура; 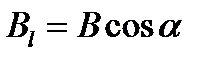 - составляющая вектора
- составляющая вектора 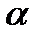 - угол между векторами
- угол между векторами 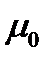 на алгебраическую сумму токов, охватываемых этим контуром:
на алгебраическую сумму токов, охватываемых этим контуром: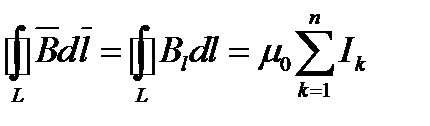


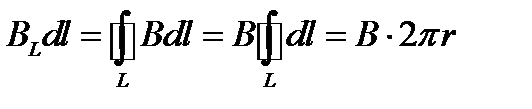



 и
и 
 электростатического поля всегда равна нулю, т.е. электростатическое поле является потенциальным. Циркуляция вектора
электростатического поля всегда равна нулю, т.е. электростатическое поле является потенциальным. Циркуляция вектора 
 - проекция вектора
- проекция вектора 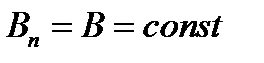 тогда
тогда


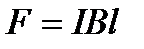
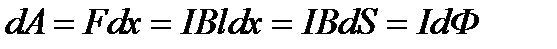
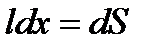 - площадь, пересекаемая проводником при его перемещении в магнитном поле;
- площадь, пересекаемая проводником при его перемещении в магнитном поле; 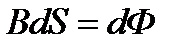 - поток вектора магнитной индукции, пронизывающей эту площадь.
- поток вектора магнитной индукции, пронизывающей эту площадь.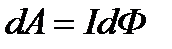
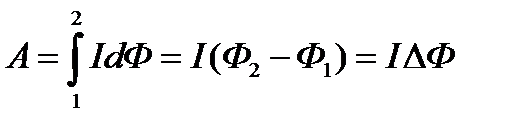
 - изменение магнитного потока, сцепленного с контуром.
- изменение магнитного потока, сцепленного с контуром. , поэтому
, поэтому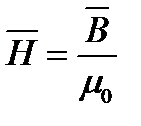
 Тл.
Тл.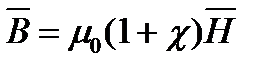 ,
, - безразмерная величина, называемая магнитной восприимчивостью вещества.
- безразмерная величина, называемая магнитной восприимчивостью вещества.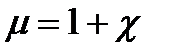 ,
, - магнитная проницаемость вещества.
- магнитная проницаемость вещества. .
.


