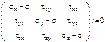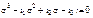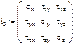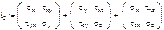Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Компоненты перемещений и деформаций в элементарном объемеСодержание книги
Поиск на нашем сайте
Компоненты перемещений и деформаций в элементарном объеме При обработке давлением металл получает остаточные значительные деформации. Если тело деформируется, то каждая точка смещается из своего первоначального положения, однако тело находится в равновесии и не имеет возможности перемещаться на 1 целое. Перемещение точки при пластической деформации происходит исключительно в следствии деформации. Если координатная точка в начальный момент соответственно равно x,y,z, а после деформации x',y',z', то параметры
Проекции перемещений на характерные оси – компоненты перемещений точки. Компоненты перемещений точек тела и их производные являются непрерывной функции координат. В общем случае элементарный прямоугольный параллелепипед после деформации изменит не только свое положение, но и форму. Длина ребер изменяется, а углы перестанут быть прямыми. В приделах малых деформаций будут иметь место наличие 2 видов деформаций: линейные относительные величина которых равна
В процессе деформации при проектировании на соответствующие оси
В процессе деформации происходит поворот соответственных ребер ab в направлении оси y на < Выразим компоненты деформации через компоненты перемещений точек элементарного параллелепипеда. Для этого выделим в окрестностях точки M деформированного тела с малыми ребрами
abcd – проекция элементарного параллелепипеда на плоскость xy до деформации. т. a совпадает с т. М После деформации данного параметра т. abcd полочим перемещение
в результате имеем (см рис) В результате деформации перемещения т. a в направлении оси x это
Точка b находится на бесконечно малом расстоянии
Аналогично перемещение т.с в направлении оси у будет отличаться от перемещения т.а в направлении оси у на бесконечно малую величину
Аналогично можно получить Перемещение точки
Аналогично определяется перемещение точки
Для малых деформаций величина
Аналогично из треугольника
Результирующая сдвиговая деформация определяется как сумма послкдних
Поступая аналогичным образом можно определить все выражения характеризующие линейные и сдвиговые деформации:
Данные уравнения носят названия уравнения Каши Величина пластических сдвигов
По аналогии с напряженным состоянием тензор деформации может быть разложен на 2 составляющие:
где
Из условия постоянства объема: Тензор деформаций Величина пластических сдвигов
По аналогии с напряженным состоянием тензор деформации может быть разложен на 2 составляющие:
где
Из условия постоянства объема:
Неразрывная деформация Компоненты деформации в уравнении Каши определяются тремя компонентами перемещения
Дифференцируем первое уравнение по Z, второе дважды по Х.
Уравнение носит название - Уравнение неразрывности деформации.
Метод линий скольжения
На начальных стадиях пластической деформации при растяжении циклического образца на его поверхности обнаруживается сетка линий, пересекающихся под прямым углом друг с другом и наклонных под углом 45º к оси образца. Эти линии (Чернова- Людерса) являются следами пересечения поверхности образца плоскостями максимальных касательных напряжений. Линии скольжения можно наблюдать также на поверхности листов, покрытых окалиной, вблизи кромки при резке, пробивке отверстий и т.п. Линии скольжения обладают рядом важных свойств, позволяющих использовать их для нахождения напряжений по объему тела при плоской и осесимметричной деформации. Зная напряжения в любой точке тела, можно определить напряжения на контактом поверхности и тем самым определить полное усилие деформации.
Дифференциальные уравнения линий скольжения следующие:
Интеграл уравнений пластичности
При переходе от одной точки на какой-либо линии скольжения к другой точке той же линии разность средних напряжений будет пропорциональна углу поворота линии скольжения и коэффициент пропорциональности равен 2k. 25 .метод сопротивления материалов пластической деф-и (метод Смирного-Алеева) Данный метод позволяет: 1)определить деформирующие усилия по заданному формоизменению. 2)опред деформ по заданной нагрузке или заданной работе внешних сил. 3)опред-ние формы тела на последов переходах по конечной его форме. Предпосылками данного метода явл: 1)При усл монотонности деформ главные осн деформ совпад с гл осями напряж при этом выполн след соотношение:
Монотонная деформация – это процесс деформации малой мат частицы когда 2) любые мат точки все время либо приближ друг к другулибо удаляются. Мощность деформ опр параметром Коэф пропорциональности
Интенсивность напряж и интенсивность деформ так же явл ф-цией работы изменен формы
Т.е устанавл функцион зависимость м/у интенсивностью напряж и интенсивностью деформ
3) напряж и деформ состояния рассм в полном соотв-ии одно с другим с использованием показателя
1)в конечно деформируемой заготовке выделяют малые частицы р-ры которых обеспечивают монотонность деформации 2)из геом соображ или непосредственно из опыта нах max удлинения или упорядочения после чего расчит логарифмич деформ 3)по найденным логарифмическим деформ определяем показатель 4)используя равенства показателей напряж и деформир сост (
5)использ усл пластичности в упрощенной форме и выраж для показателя напряж сост
После чего определ напряж состояние.
Метод баланса работ. Метод основан на законе сохранения энергии. При пластич деформ работе внешних сил на соотв им перемещениях работе внутренни+х сил
X,Y,Z – проекция сил действующих на dF,
Определяем деформирующие усилия и удельное давление при гор осадке цилиндра диаметром d и высотой h. Деформ считается осисемитричной при этом делаются допущения: 1.косат напряж 2.деформация однородная При уменьшении высоты заготовки на некоторую малу величину
Работа сопротивления деформ определ: Работа сил трения: Для определения интенсивности деформации
Т.к рассматриваемая осисеметричная задача то соотв деформ в данном ур-нии записываются:
Т.к на конт пов-ти деформ
Сварачивая предыд ур-ние пост объема получ:
Интегрирование ур-ния дает след ур-ние для перемещ в радиальном направлении
Постоянная интегрирования
А деформ
Деформ Используя выражение для интенсивности деформ вида И счит
После чего подстан в соотв интегралы
44 инварианты тензора напряжений Определяем величину главных напряжений и положение главных плоскостей по тензору напряжений в произвольной системе координат. Проекции соответствующего нормального напряжения на оси координат будут соответственно равны σax, σay, σaz. Учитывая выражения для проекций σx, σy, σz можно записать: σax = σxax + τxyay + τxzaz σay = τyxay + σyay + τyzaz σaz = τzxax + τzyay + σzaz Перенося в правую часть значения проекций нормального напряжения, получаем систему однородных уравнений. (σx – σ)ax + τxyay + τxzaz = 0 τyxay + (σy – σ)ay + τyzaz = 0 τzxax + τzyay + (σz – σ)az = 0
Так как направляющие косинусы ax, ay, az одновременно не могут быть равны 0, то равен 0 определитель данной системы:
Раскрываем данный определитель по правилу Крамера, в результате будем иметь следующее кубическое уравнение:
При выводе данного уравнения оси координат были выбраны производно, получили главное напряжение σ1, σ2, σ3. При данном напряжении составляющие имеют единственное значение, таким образом коэффициенты кубического уравнения имеют одни и те же значения независимо от выбора осей координат, т.е коэффициенты кубического уравнения (i1, i2, i3) – инвариантный, т.е. независимый при образовании осей координат. i1, i2, i3 – инвариантный тензора напряжения – линейный, квадратичный и кубический. i1 – линейный или первый инвариант тензора напряжений. i1 = σx + σy + σz i3 – кубический или третий инвариант тензора напряжений.
i2 – второй инвариант тензора напряжений – сумма миноров третьего.
для определения находятся ли точки в одном напряженном состоянии необходимо значения тензоров напряжений подставить в инварианты тензоров напряжений, i1, i2, i3, - точки будут иметь одно напряженное состояние. Если все инварианты тензора напряжений будут равны. Если на любой стадии подстановки в инварианты тензора напряжений будет недостаточно равенства, то данные точки с соответствующими координатами тензора напряжений будут находится в различных напряженных состояниях.
Компоненты перемещений и деформаций в элементарном объеме При обработке давлением металл получает остаточные значительные деформации. Если тело деформируется, то каждая точка смещается из своего первоначального положения, однако тело находится в равновесии и не имеет возможности перемещаться на 1 целое. Перемещение точки при пластической деформации происходит исключительно в следствии деформации. Если координатная точка в начальный момент соответственно равно x,y,z, а после деформации x',y',z', то параметры
Проекции перемещений на характерные оси – компоненты перемещений точки. Компоненты перемещений точек тела и их производные являются непрерывной функции координат. В общем случае элементарный прямоугольный параллелепипед после деформации изменит не только свое положение, но и форму. Длина ребер изменяется, а углы перестанут быть прямыми. В приделах малых деформаций будут иметь место наличие 2 видов деформаций: линейные относительные величина которых равна
В процессе деформации при проектировании на соответствующие оси
В процессе деформации происходит поворот соответственных ребер ab в направлении оси y на < Выразим компоненты деформации через компоненты перемещений точек элементарного параллелепипеда. Для этого выделим в окрестностях точки M деформированного тела с малыми ребрами
abcd – проекция элементарного параллелепипеда на плоскость xy до деформации. т. a совпадает с т. М После деформации данного параметра т. abcd полочим перемещение
в результате имеем (см рис) В результате деформации перемещения т. a в направлении оси x это
Точка b находится на бесконечно малом расстоянии
Аналогично перемещение т.с в направлении оси у будет отличаться от перемещения т.а в направлении оси у на бесконечно малую величину
Аналогично можно получить Перемещение точки
Аналогично определяется перемещение точки
Для малых деформаций величина
Аналогично из треугольника
Результирующая сдвиговая деформация определяется как сумма послкдних
Поступая аналогичным образом можно определить все выражения характеризующие линейные и сдвиговые деформации:
Данные уравнения носят названия уравнения Каши Величина пластических сдвигов
По аналогии с напряженным состоянием тензор деформации может быть разложен на 2 составляющие:
где
Из условия постоянства объема: Тензор деформаций Величина пластических сдвигов
По аналогии с напряженным состоянием тензор деформации может быть разложен на 2 составляющие:
где
Из условия постоянства объема:
Неразрывная деформация Компоненты деформации в уравнении Каши определяются тремя компонентами перемещения
Дифференцируем первое уравнение по Z, второе дважды по Х.
Уравнение носит название - Уравнение неразрывности деформации.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 732; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.131.51 (0.014 с.) |

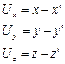
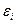 и угловых или сдвиговых
и угловых или сдвиговых 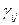



 а ребра ac на <
а ребра ac на < 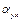 в направлении оси x причем суммарная сдвиговая деформация
в направлении оси x причем суммарная сдвиговая деформация 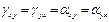
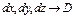 а его вершина совпадает с т A
а его вершина совпадает с т A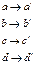
 , а в направлении оси y -
, а в направлении оси y - 
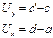
 от т.а в направлении оси х. перемещение т.
от т.а в направлении оси х. перемещение т.  будет отличаться от перемещения т.а на бесконечно малое приращение
будет отличаться от перемещения т.а на бесконечно малое приращение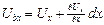
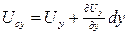

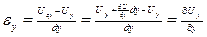
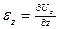
 будет отличаться от перемещения точки
будет отличаться от перемещения точки 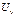 на бесконечно малую величину:
на бесконечно малую величину: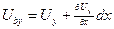
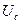
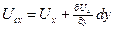
 Считается, что тангенсы угла поворота
Считается, что тангенсы угла поворота 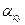 и
и  для малых деформаций равны соответствующим углам. Их треугольника
для малых деформаций равны соответствующим углам. Их треугольника 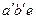 при малости угла
при малости угла 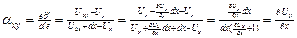
 является малой величиной < 1, т.о.
является малой величиной < 1, т.о.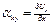
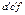 можно получить
можно получить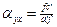 ;
; 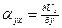

 ;
; 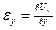 ;
; 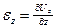 ;
; ;
; 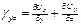 ;
; 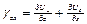
 является суммой углов поворота ребер элементарного параллелепипеда в направлении соответствующей оси. Результат изменения формы безразличен в отношении угла альфа, лишь бы их сумма оставалась постоянной и равной
является суммой углов поворота ребер элементарного параллелепипеда в направлении соответствующей оси. Результат изменения формы безразличен в отношении угла альфа, лишь бы их сумма оставалась постоянной и равной  . Это дает возможность представлять данные сдвиговых деформаций равными между собой и воспользоваться записью тензора напряжений, т.о. деформируемое состояние характеризуется некоторым тензором
. Это дает возможность представлять данные сдвиговых деформаций равными между собой и воспользоваться записью тензора напряжений, т.о. деформируемое состояние характеризуется некоторым тензором 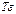 :
: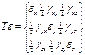
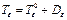 ,
,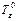 - шаровой тензор деформаций;
- шаровой тензор деформаций;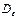 - девиатор деформаций;
- девиатор деформаций;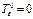
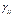 является суммой углов поворота ребер элементарного параллелепипеда в направлении соответствующей оси. Результат изменения формы безразличен в отношении угла альфа, лишь бы их сумма оставалась постоянной и равной
является суммой углов поворота ребер элементарного параллелепипеда в направлении соответствующей оси. Результат изменения формы безразличен в отношении угла альфа, лишь бы их сумма оставалась постоянной и равной 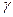 . Это дает возможность представлять данные сдвиговых деформаций равными между собой и воспользоваться записью тензора напряжений, т.о. деформируемое состояние характеризуется некоторым тензором
. Это дает возможность представлять данные сдвиговых деформаций равными между собой и воспользоваться записью тензора напряжений, т.о. деформируемое состояние характеризуется некоторым тензором 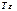 :
: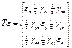
 ,
,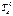 - шаровой тензор деформаций;
- шаровой тензор деформаций;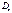 - девиатор деформаций;
- девиатор деформаций;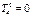 ,
, 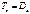
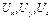 . Деформированное состояние не является произвольным, а между ними существует некоторая связь. Данная связь между линейными и сдвиговыми деформациями определяется условием совместности или неразрывности деформации.
. Деформированное состояние не является произвольным, а между ними существует некоторая связь. Данная связь между линейными и сдвиговыми деформациями определяется условием совместности или неразрывности деформации. ,
, 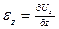

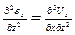 ;
; 
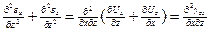
 Так как линии скольжения являются траекториями наибольших касательных напряжений и при плоской деформации имеются две равноправные плоскости максимальных касательных напряжений, получаются два семейства ортогональных линий скольжения (рис) пересекающихся с траекториями главных нормальных напряжений под углом π/4.
Так как линии скольжения являются траекториями наибольших касательных напряжений и при плоской деформации имеются две равноправные плоскости максимальных касательных напряжений, получаются два семейства ортогональных линий скольжения (рис) пересекающихся с траекториями главных нормальных напряжений под углом π/4.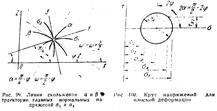

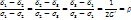
 - логарифмическая деформ
- логарифмическая деформ -коэф пропорциональности
-коэф пропорциональности -модуль пластичности 2-го рода
-модуль пластичности 2-го рода т.е растяжения, сжатия или сдвиг ост неизменной.
т.е растяжения, сжатия или сдвиг ост неизменной.
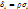
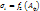

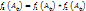

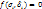
 для напряж состояния:
для напряж состояния:
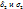 - ср главн напряж ход решения по методу Смирнова-Алеева:
- ср главн напряж ход решения по методу Смирнова-Алеева: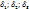

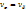 ), определ величина
), определ величина 

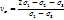
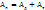
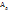 – работа деформации формы
– работа деформации формы - работа сил трения на контакте
- работа сил трения на контакте
 - интенсивность скоростей деформации
- интенсивность скоростей деформации 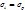
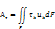
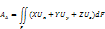
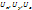 – проекции в направлениях данных осей.
– проекции в направлениях данных осей. постоянна
постоянна работа деформ определяется след образом:
работа деформ определяется след образом: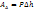
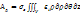
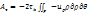
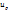 необходимо воспользоваться условием постоянства объема
необходимо воспользоваться условием постоянства объема
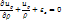
 не зависит от координаты z то при однородной деформ
не зависит от координаты z то при однородной деформ 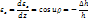


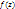 находится из граничных условий, т.е при
находится из граничных условий, т.е при 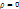 перемещение
перемещение 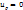 следовательно
следовательно  , т.о перемещение нах след образом
, т.о перемещение нах след образом
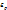

 и
и 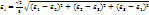
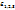 соотв деформ
соотв деформ 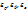 . Подстановка в последн выр-ие позволяет определить величину интенсивности деформ.
. Подстановка в последн выр-ие позволяет определить величину интенсивности деформ.
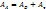

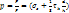 –при горячей осадке цилиндра.
–при горячей осадке цилиндра.