
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа и кинетическая энергияСодержание книги
Поиск на нашем сайте
Работой силы
где
В общем случае, когда МТ, двигаясь по криволинейной траектории, проходит путь конечной длины, этот путь можно разбить на бесконечно малые элементы, на каждом из которых сила
где Единицей работы в системе СИ является джоуль (Дж). В системе СГС единицей работы является эрг. Легко показать, что
Работа, отнесенная к единице времени, т.е.
называется мощностью. Ее единицы — эрг/с и Дж/с, или ватт (Вт). Очевидно, что
Если вспомнить, что
Этот интеграл в некоторых случаях легко вычисляется. Если масса МТ постоянна, то
где
называется кинетической энергией МТ. Отсюда, работа равна
Таким образом, работа силы при перемещении МТ равна приращению кинетической энергии этой точки. Также можно ввести кинетическую энергию системы МТ как сумму кинетических энергий МТ системы. Консервативные и неконсервативные силы. Потенциальная энергия. Примеры потенциальной энергии.
Все силы в физике подразделяются на консервативные и неконсервативные. Если силы взаимодействия зависят только от конфигурации МТ системы (т.е. их координат) и работа этих сил при перемещении системы из произвольного начального положения в произвольное конечное положение не зависит от пути перехода, а определяется только начальной и конечной конфигурациями системы, то такие силы называются консервативными.
Для консервативных сил выполняется следующее свойство. Рассмотрим перемещение МТ из точки 1 в точку 2 по двум путям: 123 и 142. Так как силы консервативные, то работы по этим двум траекториям равны: Все силы, не являющиеся консервативными, называются неконсервативными. Если на систему действуют только консервативные силы, то для такой системы можно ввести понятие потенциальной энергии. Примем какое-либо произвольное положение системы, характеризующееся заданием координат ее МТ, условно за нулевое. Работа, совершаемая консервативными силами при переходе системы из рассматриваемого положения в нулевое, называется потенциальной энергией системы в первом положении. Потенциальная энергия системы Нулевое положение произвольно. Поэтому потенциальная энергия меняется при изменении этого положения. Однако это не влияет на результаты вычислений. При изменении нулевого положения потенциальная энергия во всех точках поля сил меняется на одну и ту же постоянную, равную работе перехода из одной нулевой точки в другую. А в задаче всегда требуется работа при переходе из одной точки в другую, которая равна разности потенциальных энергий. То есть постоянная всегда вычитается и ответ не меняется. Формула для работы консервативных сил выражается формулой
то есть всегда из потенциальной энергии начальной точки вычитается потенциальная энергия конечной точки. Та же работа может быть выражена через кинетическую энергию. Приравнивая два выражения, получаем
Сумма кинетической и потенциальной энергий системы называется полной энергией системы
В системе с одними консервативными силами полная энергия системы остается неизменной. Это положение называется законом сохранения механической энергии. Приведем потенциальные энергии для некоторых сил. 1. Сила тяжести. 2. Потенциальна энергия растянутой пружины.
Если упругую энергию пружины в недеформированном состоянии считать равной нулю, то
3. Потенциальная энергия гравитационного притяжения двух МТ.
Если выбрать потенциальную энергию в бесконечности равной нулю, то
Потенциальная энергия отрицательна. Допустим теперь, что в системе кроме консервативных сил присутствуют неконсервативные, которые называются еще диссипативными. Тогда работа всех сил может быть разделена на две части: консервативную
или
То есть в этом случае полная механическая энергия уменьшается. Работа диссипативных сил переводит механическую энергию во внутреннюю тел, составляющих систему. На сегодняшний день считается, что если учесть все энергии, а не только механическую, то суммарная энергия сохраняется.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.89.130 (0.007 с.) |

 на перемещении
на перемещении  выражается формулой (см. рис.):
выражается формулой (см. рис.): ,
,
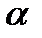 — угол между векторами
— угол между векторами  называется элементарной работой. Если вспомнить скалярное произведение, элементарная работа может быть записана в виде:
называется элементарной работой. Если вспомнить скалярное произведение, элементарная работа может быть записана в виде: .
. ,
,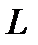 обозначает траекторию.
обозначает траекторию. .
. ,
, .
. и
и  , то формула работы принимает вид
, то формула работы принимает вид .
. и интеграл преобразуется к виду:
и интеграл преобразуется к виду: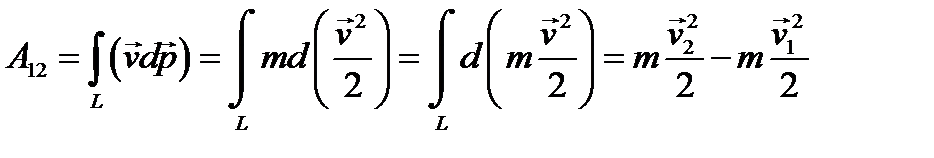 ,
, — начальная,
— начальная,  — конечная скорость МТ. Величина
— конечная скорость МТ. Величина
 .
.
 . Так кА силы зависят только от конфигурации, то
. Так кА силы зависят только от конфигурации, то  , где
, где 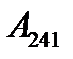 — работа, совершаемая при обратном движении по пути 241. Отсюда следует, что
— работа, совершаемая при обратном движении по пути 241. Отсюда следует, что  , то есть работа по замкнутому пути равна нулю. Свойство: работа консервативных сил по любому замкнутому пути равна нулю. К консервативным силам относятся гравитационная сила, сила тяжести, упругая сила, сила Кулона и многие другие.
, то есть работа по замкнутому пути равна нулю. Свойство: работа консервативных сил по любому замкнутому пути равна нулю. К консервативным силам относятся гравитационная сила, сила тяжести, упругая сила, сила Кулона и многие другие. является функцией только ее координат.
является функцией только ее координат. ,
, , откуда
, откуда .
. . Таким образом,
. Таким образом,  , или
, или .
.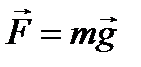 . Потенциальная энергия равна
. Потенциальная энергия равна  . Здесь
. Здесь  — высота положения МТ,
— высота положения МТ, 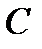 — произвольная константа. За нулевой уровень можно принять произвольный уровень, например уровень пола, уровень моря и т.д.
— произвольная константа. За нулевой уровень можно принять произвольный уровень, например уровень пола, уровень моря и т.д.  . Эта сила совершает работу
. Эта сила совершает работу .
. .
.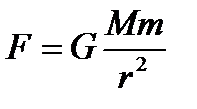 .
. .
. и диссипативную
и диссипативную  . Первая часть выражается через разность потенциальных энергий и вся работа выражается через разность кинетических энергий. Тогда
. Первая часть выражается через разность потенциальных энергий и вся работа выражается через разность кинетических энергий. Тогда ,
, .
.


