
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопередача. Макроскопическая работа. Первый закон (начало) термодинамики. Применение к изопроцессам.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Внутренняя энергия газа может быть изменена через два процесса: работу и теплопередачу.
Макроскопическая работа совершается газом или над ним. Рассмотрим газ в цилиндре с поршнем. Если поршень под воздействием давления газа перемещается на небольшую величину
где
Теплопередача заключается в том, что внутрь (и обратно) газа передается кинетическая энергия, т.е. молекулы газа изменяют среднюю скорость своего движения. При нагревании молекулы начинают двигаться быстрее, при охлаждении – медленнее. Это процесс вычисляется по формуле:
где И работа, и передача тепла имеют разные величины при разных процессах. Если собрать все в месте, то можно записать экспериментальный первый закон термодинамики
Все эти процессы должны происходить очень медленно, чтобы воздействие на газ на его границе успевало передаваться всему объему. Такие процессы называются квазистатическими. Обычно рассматривают следующие процессы: изохорический ( Кратко рассмотрим отдельные процессы. 1. Изохорический. Элементарный объем также равен нулю,
и молярная теплоемкость идеального газа при постоянном объеме
2. Изобарический.
подставляя в первый закон термодинамики, получим
Отсюда молярная теплоемкость идеального газа при постоянном давлении
3. Изотермический процесс
Формула для работы получается интегрированием. Выражаем давление из уравнения Клапейрона — Менделеева и подставляем в интеграл для работы
Теплоемкость пропорциональна отношению
4. Адиабатический процесс
Формула для работы получается из формулы для внутренней энергии:
Теплоемкость в этом процессе равна нулю,
где показатель адиабаты На рисунке справа представлены относительно друг друга графики изотермы и адиабаты.
Явления переноса. Средняя длина свободного пробега. Если система находится в неравновесном состоянии, это значит, что либо температура разная в разных частях системы, либо происходят переносы вещества и другие движения. Вследствие не вполне хаотического движения в системе начинаются явления переноса, т.е. стремление системы стать равновесной. Мы рассмотрим три вида явлений переноса.
1. Средняя длина свободного пробега. Средней длиной свободного пробега
Диффузия. Диффузией называется проникновение микрочастиц одного вещества в область пространства, занятого другим веществом. Диффузия может наблюдаться как в газах или жидкостях, так и в твердых веществах.
Если в смеси газов в одной области пространства концентрация молекул одного из них велика, а в другой, соседней области пространства мала, то будет наблюдаться проникновение молекул этого газа во вторую область, т.е. перенос массы молекул данного газа. Так движение молекулы хаотично, то скорость диффузионного проникновения из одной области в другую значительно меньше скорости их теплового движения. Рассмотрим случай, когда концентрация молекул каждого из газов в смеси зависит только от одной координаты
Здесь Если обе части уравнения умножить на массу молекулы газа, то это уравнение преобразуется к виду
где Если состояние смеси мало отличается от равновесного, то из статистической теории можно приближенно получить:
Теплопроводность. Теплопроводность — это передача энергии из одной части тела в другую. В случае газа можно рассмотреть одномерную задачу, как в диффузии. На рисунке надо заменить концентрацию на температуру
Здесь
Здесь В металлах теплопроводность обусловлена хаотическим движением электронов. Исследуется при помощи квантовой теории.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.108 (0.009 с.) |

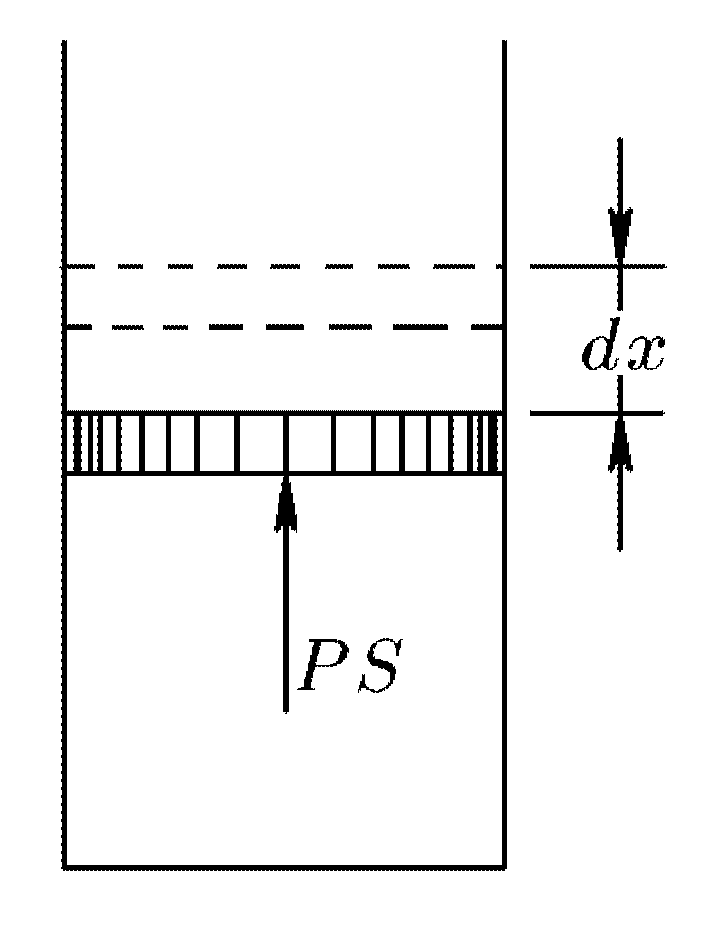
 , то работа газа может быть вычислена по формуле:
, то работа газа может быть вычислена по формуле: ,
, — площадь поверхности поршня,
— площадь поверхности поршня,  — изменение объема газа. Если изменение положения поршня конечно, то вычисление работы производится по формуле:
— изменение объема газа. Если изменение положения поршня конечно, то вычисление работы производится по формуле:
 . (см. рис.)
. (см. рис.) ,
, — молярная теплоемкость,
— молярная теплоемкость,  — удельная теплоемкость.
— удельная теплоемкость. — в дифференциальном виде,
— в дифференциальном виде,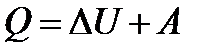 — в интегральном виде.
— в интегральном виде. ), изобарический (
), изобарический ( ), изотермический (
), изотермический ( ) и адиабатический (
) и адиабатический ( , т.е. нет передачи тепла).
, т.е. нет передачи тепла). . Работа равна нулю,
. Работа равна нулю, 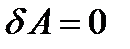 . Отсюда
. Отсюда ,
,
 .
. . Тогда, используя уравнение Клапейрона — Менделеева получаем для работы
. Тогда, используя уравнение Клапейрона — Менделеева получаем для работы  следующую формулу
следующую формулу и
и .
. .
. . Поскольку температура не меняется, то не меняется внутренняя энергия и все тепло превращается в работу
. Поскольку температура не меняется, то не меняется внутренняя энергия и все тепло превращается в работу .
. .
.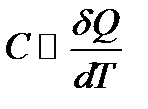 и при
и при 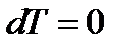 обращается в бесконечность
обращается в бесконечность  .
. . Работа газа совершается за счет изменения внутренней энергии. То есть при адиабатическом расширении газ охлаждается
. Работа газа совершается за счет изменения внутренней энергии. То есть при адиабатическом расширении газ охлаждается .
. .
.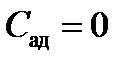 . Из первого закона термодинамики и уравнения Клапейрона — Менделеева можно получить уравнение адиабаты в
. Из первого закона термодинамики и уравнения Клапейрона — Менделеева можно получить уравнение адиабаты в  координатах:
координатах: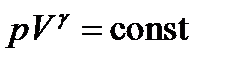 ,
, . Для газов с разными степенями свободы этот показатель разный.
. Для газов с разными степенями свободы этот показатель разный.
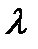 называется среднее расстояние, которое пролетает молекула от одного столкновения до следующего. Вычисляется она по формуле:
называется среднее расстояние, которое пролетает молекула от одного столкновения до следующего. Вычисляется она по формуле: ,
,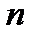 — концентрация молекул,
— концентрация молекул, 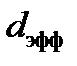 — эффективный диаметр молекулы,
— эффективный диаметр молекулы,  — площадь эффективного сечения, в которое должна попасть молекула, чтобы столкновение произошло.
— площадь эффективного сечения, в которое должна попасть молекула, чтобы столкновение произошло. 
 . Если мысленно выделить в пространстве некоторую площадку
. Если мысленно выделить в пространстве некоторую площадку  , ортогональную к оси
, ортогональную к оси  , то поток молекул газа через эту площадку (число молекул, проходящих в единицу времени), как показывает опыт, будет равен
, то поток молекул газа через эту площадку (число молекул, проходящих в единицу времени), как показывает опыт, будет равен .
. называется коэффициентом диффузии, а производная
называется коэффициентом диффузии, а производная  называется градиентом концентрации молекул газа. В трехмерном случае эта производная превращается в вектор градиента. Знак минус в формуле подчеркивает тот факт, что перенос молекул всегда происходит в направлении, противоположном направлению возрастания концентрации.
называется градиентом концентрации молекул газа. В трехмерном случае эта производная превращается в вектор градиента. Знак минус в формуле подчеркивает тот факт, что перенос молекул всегда происходит в направлении, противоположном направлению возрастания концентрации. ,
, переносимая в единицу времени масса, а
переносимая в единицу времени масса, а 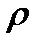 обозначает плотность газа в данном месте. В таком виде уравнение представляет собой закон Фика. Коэффициент диффузии
обозначает плотность газа в данном месте. В таком виде уравнение представляет собой закон Фика. Коэффициент диффузии  .
. и поток частиц на поток тепла
и поток частиц на поток тепла  . Тогда имеем для теплопроводности закон Фурье
. Тогда имеем для теплопроводности закон Фурье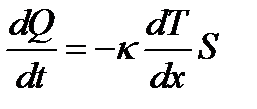 .
. (каппа) — коэффициент теплопроводности,
(каппа) — коэффициент теплопроводности,  — градиент температуры. Знак минус показывает, что тепло передается от более горячей области вещества к более холодной. В случае почти равновесия в газе
— градиент температуры. Знак минус показывает, что тепло передается от более горячей области вещества к более холодной. В случае почти равновесия в газе  .
. — плотность газа,
— плотность газа,  — удельная теплоемкость газа при постоянном объеме. В СИ коэффициент теплопроводности измеряется в
— удельная теплоемкость газа при постоянном объеме. В СИ коэффициент теплопроводности измеряется в 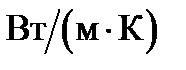 .
.


