
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия заряженного конденсатора. Плотность электрической энергии. Энергия системы заряженных тел.Содержание книги
Поиск на нашем сайте
Вычислим энергию заряженного конденсатора. Пусть первоначально обкладки конденсатора не заряжены. Будем переносить положительный (ил отрицательный) заряд малыми порциями
где
Интегрируя, получим
Энергия взаимодействия точечных зарядов получается при переносе их из бесконечности в то место, где они расположены. Получается формула
где штрих при потенциале означает, что при его расчете учитываются все заряды, кроме того, на который они действуют. Для непрерывно распределенных зарядов получается интеграл по объему, занимаемому зарядами
где Так как электрическое поле конденсатора сконцентрировано внутри и однородно, то можно считать, что энергия поля тоже распределена внутри конденсатора. Если разделить вычисленную энергию на объем
Можно показать, что эта формула верна при любой конфигурации электрического поля.
Электромагнитная индукция Электромагнитная индукция была открыта Фарадеем в 1831 г. Для демонстрации этого явления возьмем неподвижный магнит и проволочную катушку, концы которой соединены с гальванометром. Если катушку приближать к одному из полюсов магнита, то во время движения стрелка гальванометра отклоняется — в катушке возбуждается электрический ток. При движении катушки в обратном направлении направление тока меняется на противоположное. Магнит можно заменить другой катушкой с током или электромагнитом. Этот ток называется индукционным током, а само явление — электромагнитной индукцией.
Возбуждение электрического тока при движении проводника в магнитном поле объясняется действием силы Лоренца, возникающей при движении проводника. Рассмотрим простейший случай, когда два параллельных провода Возникает напряженность стороннего поля, равная
К этой формуле необходимо добавить правило, которое позволяет быстро определять направление индукционного тока. Оно носит название правило Ленца и гласит: Индукционный ток всегда имеет такое направление, что его собственное магнитное поле препятствует изменению магнитного потока, его вызывающего. Возникающий в проводнике ток исчезает потому, что существует сопротивление. Если бы сопротивления не было, то раз возникнув, ток продолжался бесконечно долго. Такие условия встречаются в сверхпроводниках. Кроме этого, закон электромагнитной индукции позволяет объяснить диамагнетизм в атомах и молекулах. Магнитное поле возникшего дополнительного тока направлено в сторону, противоположную внешнему полю. И так как сопротивления в молекулах нет, то оно не исчезает. Магнитный поток После предварительного рассмотрения сформулируем закон в общем виде. Как и в случае электрического поля можно ввести поток индукции магнитного поля:
Здесь
И напоминаю теорему Гаусса для магнитного потока:
Необходимо отметить, что поверхность, на которой вычисляется поток индукции, можно деформировать. Для доказательства рассмотрим рисунок справа. На нем представлен разрез контура (точки
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.45.223 (0.006 с.) |

 с одной обкладки на другую. Для переноса необходимо совершить работу против электрического поля;
с одной обкладки на другую. Для переноса необходимо совершить работу против электрического поля; ,
, — мгновенное значение разности потенциалов между обкладками. Эта работа полностью идет на увеличение электрической энергии конденсатора
— мгновенное значение разности потенциалов между обкладками. Эта работа полностью идет на увеличение электрической энергии конденсатора .
. .
. ,
, ,
, — объемная плотность зарядов.
— объемная плотность зарядов. , где
, где  — площадь обкладки, то получится объемная плотность энергии
— площадь обкладки, то получится объемная плотность энергии .
.
 и
и  помещены в постоянное однородное магнитное поле, перпендикулярное к плоскости рисунка и направленное на нас. (см. рис.) Слева провода
помещены в постоянное однородное магнитное поле, перпендикулярное к плоскости рисунка и направленное на нас. (см. рис.) Слева провода  . Когда мостик движется вправо со скоростью
. Когда мостик движется вправо со скоростью  , вместе с ним движутся электроны и положительные ионы. На каждый движущийся заряд
, вместе с ним движутся электроны и положительные ионы. На каждый движущийся заряд  в магнитном поле действует сила Лоренца
в магнитном поле действует сила Лоренца  . На положительный ион она действует вниз, на отрицательный электрон — вверх. Электроны начнут перемещаться вверх и там будет скапливаться отрицательный заряд, внизу останется больше положительных ионов. То есть положительные и отрицательные заряды разделяются, возникает электрическое поле вдоль мостика, и потечет ток. Этот ток называется индукционным. Ток потечет и в других частях контура
. На положительный ион она действует вниз, на отрицательный электрон — вверх. Электроны начнут перемещаться вверх и там будет скапливаться отрицательный заряд, внизу останется больше положительных ионов. То есть положительные и отрицательные заряды разделяются, возникает электрическое поле вдоль мостика, и потечет ток. Этот ток называется индукционным. Ток потечет и в других частях контура  . На рисунке токи изображены сплошными стрелками.
. На рисунке токи изображены сплошными стрелками. .Электродвижущая сила, создаваемая этим полем, называется электродвижущей силой индукции и обозначается
.Электродвижущая сила, создаваемая этим полем, называется электродвижущей силой индукции и обозначается  . В рассматриваемом случае
. В рассматриваемом случае  , где
, где  — длина мостика. Знак минус поставлен потому, что стороннее поле
— длина мостика. Знак минус поставлен потому, что стороннее поле 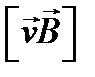 направлено против положительного обхода контура, определяемого вектором
направлено против положительного обхода контура, определяемого вектором  по правилу правого винта. Величина
по правилу правого винта. Величина  есть приращение площади контура
есть приращение площади контура  в единицу времени. Поэтому
в единицу времени. Поэтому  равна
равна  , т.е. скорости приращения магнитного потока, пронизывающего площадь контура
, т.е. скорости приращения магнитного потока, пронизывающего площадь контура  .
. .
.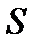 — площадь контура, через который проходит магнитное поле,
— площадь контура, через который проходит магнитное поле,  — нормаль к площадке, ограниченной контуром. Скалярное произведение
— нормаль к площадке, ограниченной контуром. Скалярное произведение  может быть заменено на
может быть заменено на  , где
, где  — угол между направлениями вектора индукции и нормалью. Если магнитная индукция меняется по величине и направлению, то формула для потока переходит в следующую
— угол между направлениями вектора индукции и нормалью. Если магнитная индукция меняется по величине и направлению, то формула для потока переходит в следующую .
.
 .
. и
и  ) и разрез двух поверхностей
) и разрез двух поверхностей  (кривые
(кривые  и
и  ). Крест в точке
). Крест в точке  и точка — в
и точка — в  показывают направление обхода контура, которое связано правым винтом с направлением нормалей на поверхности. Так как поток вектора индукции через замкнутую поверхность равен нулю, то потоки по отдельным поверхностям
показывают направление обхода контура, которое связано правым винтом с направлением нормалей на поверхности. Так как поток вектора индукции через замкнутую поверхность равен нулю, то потоки по отдельным поверхностям 


