
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитное поле равномерно движущегося заряда. Закон био—савара.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Токи и движущиеся точечные заряды сами создают магнитное поле. Начнем с движущегося точечного заряда
где Как и в случае закона Ампера, можно перейти от одного движущегося заряда к току. Вычисления приводят к формуле
Эта формула выражает закон Био—Савара. (см. рисунок). Полное поле получается интегрированием этой формулы по всем токам
Эти выражения применимы только для постоянных токов. Магнитное поле бесконечного прямого провода и витка с током. С помощью этого закона можно получить конечные формулы для некоторых проводников. 1. Бесконечный прямолинейный провод, по которому течет ток
где Если расположить рядом два параллельных тока, то один ток создает в месте, где находится другой, то можно вычислить силу, с которой первый ток действует на участок второго тока длиной
где 2. Индукция магнитного поля кругового тока в центре приводит к формуле
где Кроме вектора магнитной индукции вектор напряженности магнитного поля Для витка с током можно также ввести понятия ие магнитного момента, по аналогии с электрическим дипольным моментов. Вектор магнитного момента
где
Теорема Гаусса для магнитного поля. Циркуляция магнитного поля. Теорема Гаусса для магнитного поля выглядит очень просто:
или в дифференциальной форме
Эти уравнения интерпретируются как отсутствие магнитных зарядов. Экспериментально эти заряды не найдены.
Циркуляция вектора
где сумма справа распространяется на все токи, которое пересекают площадку, ограниченную контуром. Токи входят со своими знаками, Положительный ток образует правый винт с направлением обхода контура, а отрицательный — левый винт. Для варианта на рисунке сумма справа выглядит как В дифференциальной форме циркуляция ожжет быть представлена в виде
где левая часть формулы есть
Циркуляция может быть использована для вычисления магнитного поля в соленоиде:
где Магнитное поле в веществе. Различные типы магнетиков. Внутри вещества все токи являются замкнутыми (движение электронов в атомах и молекулах) и образуют отдельные контуры. Каждый контур обладает своим магнитным моментом. Для характеристики магнитных свойств вещества вводится понятие намагниченности. Намагниченностью называется вектор, равный магнитному моменту единицы объема вещества, то есть
где
где
или
Для однородной среды:
Здесь введен новый коэффициент
Различные типы магнетиков.
Все вещества являются магнетиками, т.е. подвержены влиянию магнитного поля. Они подразделяются, во-первых, на слабомагнитные, у которых Слабомагнитные вещества в свою очередь делятся на парамагнетики, у которых Сильномагнитные вещества не только обладают
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1959; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.192.174 (0.006 с.) |

 , ограничиваясь при этом равномерными движениями с малыми скоростями. Такой закон является обобщением опытных фактов и выражается формулой
, ограничиваясь при этом равномерными движениями с малыми скоростями. Такой закон является обобщением опытных фактов и выражается формулой ,
, — радиус-вектор, проведенный от заряда
— радиус-вектор, проведенный от заряда 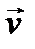 — скорость движения частицы,
— скорость движения частицы,  — магнитная постоянная, необходимая в системе СИ.
— магнитная постоянная, необходимая в системе СИ.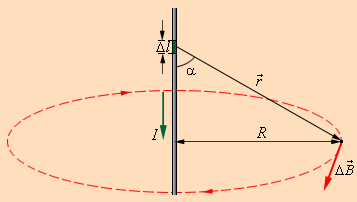
 .
. .
. . Интегрирование формулы приводит к результату
. Интегрирование формулы приводит к результату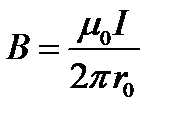 ,
, — расстояние от точки наблюдения до проводника с током.
— расстояние от точки наблюдения до проводника с током. :
: ,
, ). Если токи равны по 1 А,
). Если токи равны по 1 А,  , то сила должна быть
, то сила должна быть 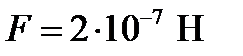 .
. ,
,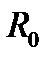 — радиус кругового тока.
— радиус кругового тока.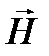 . В вакууме оба вектора связаны простой формулой
. В вакууме оба вектора связаны простой формулой  .
. произвольного контура с током
произвольного контура с током 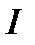 равен
равен ,
, — площадь витка,
— площадь витка,  — единичный вектор нормали к плоскости витка. Если вращать ток в направлении его движения, то вектор нормали показывает направление вкручивания правого винта. Для круглого витка можно записать
— единичный вектор нормали к плоскости витка. Если вращать ток в направлении его движения, то вектор нормали показывает направление вкручивания правого винта. Для круглого витка можно записать .
. ,
, .
.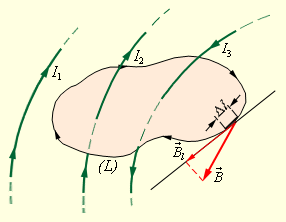
 (см. рисунок) выражается формулой
(см. рисунок) выражается формулой ,
, . Ток
. Ток  не входит в сумму, так как не пересекает площадку.
не входит в сумму, так как не пересекает площадку. ,
,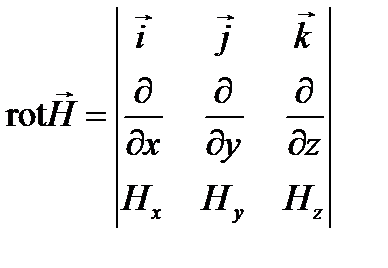 .
. ,
, — число витков на единицу длины соленоида.
— число витков на единицу длины соленоида.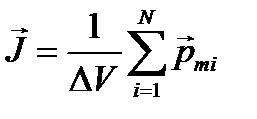 ,
, — число молекул в малом объеме
— число молекул в малом объеме 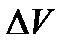 . При малых значениях внешнего магнитного поля вектор намагниченности линейно зависит от напряженности магнитного поля и в случае однородного вещества равна
. При малых значениях внешнего магнитного поля вектор намагниченности линейно зависит от напряженности магнитного поля и в случае однородного вещества равна ,
, — магнитная восприимчивость. Общее магнитное поле складывается из внешнего
— магнитная восприимчивость. Общее магнитное поле складывается из внешнего 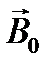 и поля создаваемого токами внутри вещества
и поля создаваемого токами внутри вещества  :
: ,
, .
. .
.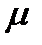 , называемый относительной магнитной проницаемостью вещества.
, называемый относительной магнитной проницаемостью вещества.


