
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эффект Холла в полупроводникахСодержание книги Поиск на нашем сайте
РОССИЙСКОЙ ФЕДЕРАЦИИ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (МИИТ) _____________________________________________________________ Кафедра «Физика-2»
Утверждено редакционно-издательским советом университета
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ
по дисциплине «Физика» для студентов всех специальностей
Работы 47, 50, 51, 52, 55
Под редакцией профессора С.М. Кокина и профессора В.А. Никитенко Москва - 2004
УДК 539.2 М-54
Методические указания к лабораторным работам по дисциплине «Физика»/ Под ред. проф. С.М. Кокина, проф. В.А. Никитенко. – переизд., доп. – М.: МИИТ, 2004. – 48 с.
Сборник методических указаний для выполнения студентами лабораторных работ по разделу «Физика твердого тела» включает в себя описание и порядок выполнения пяти лабораторных работ, предназначенных для студентов первого и второго курса всех специальностей. Методические указания к лабораторным работам составили: В.А. Селезнев (№52), В.А. Никитенко и С.В. Мухин (№ 55), переработали: Е.А. Серов (№47), В.А. Селезнев (№ 50), С.М. Кокин (№ 51). Работу № 51 в МИИТе впервые поставил доц. Е.И. Тимошкин.
© Московский государственный университет путей сообщения (МИИТ), 2004
РАБОТА 47
ЭФФЕКТ ХОЛЛА В ПОЛУПРОВОДНИКАХ Цель работы. Измерение холловской разности потенциалов в полупроводниковой пластине и определение концентрации, подвижности и знака носителей заряда, участвующих в токе. Введение
Эффект Холла заключается в возникновении поперечной разности потенциалов при пропускании тока через металлическую или полупроводниковую пластинку, помещенную в магнитное поле, направленное под некоторым углом к направлению тока. Обычно вектор индукции магнитного поля Разность потенциалов возникает, как это показано на рис. 1, между точками А и А 1, лежащими на прямой, перпендикулярной как к вектору Классическая электронная теория объясняет эффект Холла следующим образом: поток электрических зарядов, попадая в магнитное поле, отклоняется от первоначального направления своего движения под действием силы Лоренца
где q – величина заряда,
Рис.1
При этом одна из боковых сторон пластинки получает отрицательный заряд, в то время как противоположная сторона заряжается равным ему по величине положительным зарядом. Накопление зарядов происходит до тех пор, пока сила, действующая на электрический заряд со стороны холловского электрического поля, не уравновесит силу Лоренца:
Таким образом, напряженность поперечного холловского электрического поля
Если векторы
где d— расстояние AA1 (см. рис. 1). Средняя скорость направленного движения носителей тока связана с плотностью тока
Выразив плотность тока через силу тока
(
где
Коэффициент Формула (7) получается без учета закона распределения электронов по скоростям. Более точный расчет с учетом закона распределения носителей по скоростям в рамках классической статистики приводит к выражению для постоянной Холла
Для атомных полупроводников, например, для кремния, Для полупроводников с ионной связью, к которым относится рассматриваемое в данной работе интерметаллическое соединение арсенид галлия, Соотношение (6) позволяет определить постоянную Холла
Если Важной характеристикой полупроводника является подвижность в нем носителей заряда, под которой подразумевается средняя скорость, приобретаемая носителем в поле, напряженность которого равна единице. Если в поле напряженностью
Используя связь между плотностью тока, напряженностью электрического поля и проводимостью
Из соотношений (7) и (11) следует
Таким образом, для определения подвижности носителя Знак постоянной Холла определяется знаком носителей заряда. У полупроводников постоянная Холла может быть отрицательной и положительной, так как существует два типа проводимости. У полупроводников с электронной проводимостью (полупроводников n-типа) перемещаются электроны, и знак постоянной Холла отрицателен. У другого типа полупроводников электропроводность осуществляется положительными зарядами или так называемыми «дырками». Такие полупроводники называются дырочными (полупроводниками р-типа). Они имеют положительный знак постоянной Холла. При этом
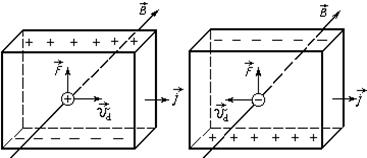
Рис. 2
Зависимость знака постоянной Холла от знака носителей заряда, создающих в данном веществе UH можно понять из рис. 2, на котором демонстрируется эффект Холла для образцов с положительными и отрицательными носителями. Направление силы Лоренца изменяется на противоположное как при изменении направления движения зарядов, так и при изменении их знака. Следовательно, при одинаковом направлении тока и магнитной индукции В сила Лоренца, действующая на положительные и отрицательные носители, имеет одинаковое направление. Поэтому в случае положительных носителей потенциал верхней грани (см. рис. 2) выше, чем нижней, а в случае отрицательных носителей – ниже. Таким образом, определив знак холловской разности потенциалов, можно установить знак носителей заряда, участвующих в токе.
Рис. 3
T 10
Рис. 4
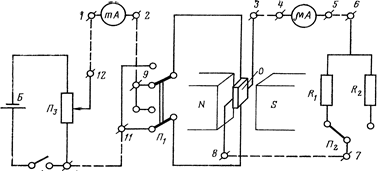
В данной работе исследуется ЭДС Холла (поперечная разность потенциалов) в зависимости от величины протекающего по образцу продольного тока I при постоянном значении внешнего магнитного поля. Для определения ЭДС Холла используют метод, основанный на измерении с помощью микроамперметра mА, нагружаемого на два различных сопротивления r1 и r2 двух токов i1 и i2 в холловской цепи. Расчет ЭДС Холла производится по формуле
Формула получается из решения уравнения Кирхгофа для холловской цепи
где R – нагрузочное сопротивление (R1 или R2); RK – контактное сопротивление; Ri – сопротивление образца между холловскими электродами; R mA – сопротивление микроамперметра. Подставляя вместо R значения R1 и R2, получим систему двух уравнений:
Если выбирать значения токов i1 и i2 достаточно близкими друг другу, то контактное сопротивление RK можно считать постоянным при измерениях. Решая систему уравнений (15), получим расчетную формулу (13). Для исключения паразитных ЭДС, возникающих из-за наличия асимметрии холловских контактов и температурного градиента в образце, окончательное значение ЭДС Холла рассчитывается как среднее арифметическое из четырех измерений: двух при разном направлении продольного тока и двух при разном направлении магнитного поля. Порядок выполнения работы
1.Собрать схему с помощью добавочных гибких проводов. При заэкранированном исследуемом образце О включить тумблер Т, установить потенциометром П 3 максимально возможное значение продольного тока, показываемое миллиамперметром мА, и по показаниям микроамперметра m А убедиться в возможном наличии паразитных ЭДС. После этого продольный ток свести потенциометром П 3 до минимально возможного значения, сдвинуть рукояткой Р 2 магнитный экран Э с исследуемого образца О и тем самым подготовить образец для измерения ЭДС Холла в поле постоянного магнита. 2. Поставить переключатель P 1 в нижнее положение и установить продольный ток величиной 2 мА. Микроамперметром измерить два значения тока в холловской цепи, включая с помощью переключателя П 2 сопротивления R 1 и R 2. 3. Установить переключатель П 1 в верхнее положение и провести измерения, указанные в п. 2. 4. Рукояткой P 1 повернуть образец на 180°, изменив тем самым направление магнитного поля на противоположное, и провести измерения, указанные в пп. 2, 3. 5. Весь процесс измерений, указанный в пп. 2 ¸ 4, выполнить для значений продольного тока в 4, 6, 8 и 10 мА, т. е. для каждого значения продольного тока снимается 4 значения токов через образец. Полученные данные занести в таблицу. Выключить тумблер Т и разобрать схему.
6. Рассчитать ЭДС Холла по формуле (13), взяв значения сопротивлений R 1 и R 2 из таблицы на приборе Тб; данные занести в таблицу. 7. Построить график 8. Вычислить значение постоянной Холла, концентрации и подвижности носителей заряда. Значение индукции магнитного поля, удельного сопротивления арсенида галлия и толщины образца указаны на приборе в табл. Тб
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем заключается эффект Холла? 2. Что называется подвижностью электронов и дырок и как она зависит от температуры? 3. Чему равна сила Лоренца и как определить ее направление? 4. Как определить знак носителей тока при помощи эффекта Холла? 5. Укажите различные применения эффекта Холла.
СПИСОК ЛИТЕРАТУРЫ
1. Савельев И.В. Курс общей физики. – М., Наука, 1987.—Т. 2, § 73. 2. Епифанов Г.И. Физика твердого тела. – М.: Высшая школа, 1977. 3. Епифанов Г.И. Физические основы микроэлектроники. – М.: «Советское радио», 1971. – Гл. 7. § 10.
РАБОТА 50
Введение Электромагнитное излучение, испускаемое нагретым телом, находящимся в состоянии термодинамического равновесия, называется тепловым (или температурным) излучением. При тепловом излучении внутренняя энергия тела, обусловленная движением составляющих его частиц, непрерывно переходит в энергию испускаемых ими электромагнитных волн. Полной испускательной способностью (энергетической светимостью) тела R Т называется энергия, испускаемая единицей поверхности тела по всем направлениям в единицу времени в виде электромагнитных волн с разной длиной волны. Она определяется с помощью соотношения
где r l,T – спектральная испускательная способность, т. е. количество энергии, излучаемой по всем направлениям за единицу времени с единицы поверхности источника в единичном интервале длин волн. Все тела, находящиеся при температуре, отличной от температуры абсолютного нуля, излучают в пространство лучистую энергию. Однако различные тела при одинаковой температуре излучают не одинаковые количества энергии. Наибольшее количество энергии излучает так называемое абсолютно черное тело (а. ч. т.), обладающее максимально возможной испускательной способностью при данной температуре. (Абсолютно черное тело – это понятие, означающее тело, которое полностью поглощает падающее на него излучение. Абсолютно черных тел в природе не существует, но имеются устройства, хорошо моделирующие а. ч. т.). Испускательные способности всех остальных тел меньше, чем у абсолютно черного тела. Полная испускательная способность абсолютно черного тела определяется температурой а. ч. т. в соответствии с законом Стефана-Больцмана:
R Tа.ч.т. = s T 4, (2)
где s – постоянная Стефана-Больцмана (s = 5,67×10-8 Вт × м-2× град-4); Т – абсолютная термодинамическая температура. Этот закон можно использовать для измерения температуры нагретых тел. Приборы для измерения температуры, основанные на измерении теплового излучения нагретых тел, называются пирометрами. Поскольку интенсивность теплового излучения резко убывает с уменьшением температуры тела, то пирометры применяются, в основном, для измерения относительно высоких температур. Так, при t >1000°С они играют уже основную роль, а при t >3000°С становятся практически единственными приборами измерения температуры. Наиболее чувствительными (но не очень точными) являются радиационные пирометры или пирометры суммарного излучения. В таких приборах излучение исследуемого нагретого тела фокусируется на термоприемник пирометра, который преобразует энергию излучения в электрическую, измеряемую с помощью электроизмерительного прибора. Если предварительно провести градуировку электроизмерительного прибора относительно известных температур а. ч. т., то в дальнейшем можно измерять этим пирометром температуры других а. ч. т. Однако, если с помощью отградуированного таким образом пирометра измеряется температура не абсолютно черного, а реального тела, то полученное значение температуры Т Р будет отличаться от действительной температуры тела Т (Т Р будет меньше Т, так как испускательная способность нечерного тела всегда меньше испускательной способности а. ч. т.). Температуру Т Р называют радиационной температурой тела.Она равна такой температуре а. ч. т., при которой его полная испускательная способность R Tра.ч.т.равна полной испускательной способности R T исследуемого тела при его действительной температуре Т: R T = R Tра.ч.т. = s T р4. Если определить полный коэффициент поглощения тела aТ (коффициент черноты) как отношение полной испускательной способности данного тела к полной испускательной способности а. ч. т. при одной и той же температуре Т: aТ = R T / R Tа.ч.т.< 1,
то между истинной (термодинамической) Т и радиационной Т Ртемпературами можно установить соотношение:
Т = Т Р/ Зная величину aТ для данного тела, можно по известной радиационной температуре определить его истинную температуру. Например, для вольфрамовой спирали лампы накаливания в диапазоне изменения радиационной температуры от 1100 до 1400 К aТ = 0,24±0,01. Порядок выполнения работы
1. Навести пирометр (ПИР) на источник излучения так, чтобы центры термобатареи и изображения излучателя совпадали (смотреть через отверстие в торце пирометра). 2. Установить необходимое значение падения напряжения на лампе, регулируя выходное напряжение источника питания (И.П.). Записать показания вольтметра V и амперметра A в таблицу. Замеры записывать после установления стационарного режима в цепи лампы, т. е. через некоторое время после установления напряжения.
3. Для каждого значения напряжения и силы тока, протекающего через лампу, записать показание милливольтметра mV пирометра. Измерение силы тока и показаний милливольтметра пирометра провести при увеличении и уменьшении напряжения на лампе. По среднему значению показаний пирометра для каждого значения напряжения на лампе найти ее радиационную температуру, пользуясь градуировочным графиком, помещенном на стенде установки. Зависимость полной испускательной способности вольфрама (материал спирали лампы накаливания) от температуры найдем следующим образом. Связь между радиационной температурой и полной испускательной способностью вольфрама R T можно записать в виде, аналогичном соотношению (2) R T ~ T Р n, (4) где n - константа, n»4. Поскольку при высокой температуре подводимая к исследуемой спирали лампы мощность N пропорциональна ее полной испускательной способности, то N ~ R T ~ T Р n, иначе: N = C R T = C'T P n, (5) где С, С', – некие коэффициенты пропорциональности. Чтобы получить искомую зависимость (4), необходимо: а) рассчитать мощность, потребляемую лампой по формуле N = I U; (6) б) построить график зависимости lg N от lg T P, в) определить n в уравнении (5): lg N = lg C' + n lg T P, (7) по тангенсу угла наклона полученного графика к оси абсцисс, т. е. как отношение разности значений ординат к разности значений абсцисс двух выбранных точек графика.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что называется тепловым излучением? 2. Что называется спектральной испускательной способностью и полной испускательной способностью тела? 3. Какие тела называются абсолютно черными телами? 4. Какие законы теплового излучения вы знаете? В чем сущность этих законов? 5. Что понимается под радиационной температурой тела? 6. Нарисуйте блок-схему радиационного пирометра. 7. В чем заключается принцип измерения температуры тела с помощью радиационного пирометра? СПИСОК ЛИТЕРАТУРЫ 1. Ландсберг Г. С. Оптика. – Гостехиздат, 1970. 2. Савельев И. В. Курс общей физики. – М.: Наука, 1979. – Т. 3. 3. Физический практикум / Под ред. В. М. Ивероновой. – М.: Наука, 1968 – Т. 2. 4. Детлаф А. А., Яворский Б. М. Курс физики. – М.: Высшая школа, 1989. РАБОТА 51
Рис. 1
Рассмотрим механизм и особенности проводимости полупроводников, исходя из представлений зонной теории. Энергетические зоны полупроводника с собственной проводимостью (собственного полупроводника) при абсолютном нуле температуры изображены на рис.1. Над заполненной электронами валентной зоной располагается совершенно свободная зона проводимости. Валентная зона и зона проводимости разделены запрещенной зоной энергий, характеризующейся шириной Еg. В валентной зоне нет свободных энергетических состояний, а это означает, что электрическое поле не может придать электронам этой зоны добавочную кинетическую энергию и заставить их двигаться в определённом направлении: такой образец не проводит электрический ток и ведёт себя подобно диэлектрику. Собственная проводимость возникает под влиянием какого-либо внешнего воздействия (нагрева, облучения, сильного электрического поля), когда часть электронов с верхних уровней валентной зоны, оказывается способной перейти в зону проводимости (переходы 1 на рис. 1). Понятно, что для этого таким электронам нужно сообщить дополнительную энергию, равную, как минимум, ширине запрещенной зоны Еg данного полупроводника. Оказавшись в зоне проводимости, в которой очень много разрешенных уровней энергии, электроны уже могут ускоряться полем: при включении образца в электрическую цепь по нему начинает идти ток. У потолка валентной зоны после ухода электрона образуется вакантное энергетическое состояние. Это состояние может занять другой электрон валентной зоны, ускоренный электрическим полем до требуемой энергии. Но после этого окажется свободным его «старое» состояние, которое теперь сможет занять третий электрон, ускоренный полем, и т. д. Можно следить за поочерёдным переходом в освобождающиеся состояния (и о движении по кристаллу) одного электрона за другим, а можно говорить о миграции по кристаллу свободного энергетического состояния. Вакантное энергетическое состояние в валентной зоне называется дыркой; его удобно рассматривать как движущуюся по кристаллу квазичастицу, имеющую такой же по величине заряд, как у электрона, но противоположный ему по знаку (положительный). Таким образом, в создании собственной электропроводимости полупроводников участвуют два вида носителей заряда - электроны и дырки. Величина удельной электропроводности s собственного полупроводника зависит от их концентрации п (числа в единице объема) и подвижности u, под которой понимается средняя дрейфовая скорость, приобретаемая электронами и дырками в электрическом поле единичной напряженности. Очевидно, что в собственном полупроводнике концентрация дырок равна концентрации электронов в зоне проводимости, и собственная электропроводность полупроводника s = en(un+ up),(1)
где e - заряд электрона; un и up - подвижности электронов и дырок соответственно. При увеличении температуры число электронов, способных перейти запрещенную зону, увеличивается, и поэтому их концентрация в зоне проводимости собственного полупроводника возрастает: n ~ exp [ - Еg /( 2 kT) ], (2) где Еg – ширина запрещенной зоны; k = 1,38×10-23 Дж/К – постоянная Больцмана, T – абсолютная температура. Подвижность носителей заряда зависит от температуры значительно слабее, чем их концентрация. Вследствие этого зависимость s(T) собственного полупроводника определяется зависимостью п(Т ) и является экспоненциальной: s(T) = s0C ×exp [ - Еg /( 2 kT) ], (3) где s0C - слабо зависящий от температуры множитель. Из формулы (3) следует, что логарифм удельной электропроводности ln [ s(T) ] является линейной функцией от 1/2 kТ: ln [ s(T) ] = ln [ s0C ]- или, введя обозначения y = ln [ s(T) ], x = 1/2 kТ и a = ln [ s0C ]: y = a - Еg×x. (4)
Графиком зависимости y(x) является прямая; это означает, что ширину запрещенной зоны можно вычислить, определив тангенс угла наклона данной прямой к оси абсцисс. До сих пор мы говорили о собственной проводимости полупроводника, однако, введение в него примеси может существенным образом сказаться на его электрических свойствах. Для выяснения механизма примесной проводимости рассмотрим, что происходит при введении атомов из пятой и третьей групп таблицы Менделеева в германий - элемент четвёртой группы. На внешней электронной орбите атомы германия (Ge) имеют по четыре валентных электрона; при объединении атомов в кристаллическую решётку возникают ковалентные связи: электроны внешних орбит у соседних атомов попарно обобществляются. Но если в такую решётку ввести примесный атом с валентностью, равной пяти, например, фосфор (P), мышьяк (As) или сурьму (Sb), то, заняв в ней место одного из основных атомов и отдав четыре электрона соседям, такой атом всё равно будет иметь один «лишний» электрон, который способен оторваться от «хозяина» и свободно перемещаться по кристаллу германия. В частности, он может ускоряться электрическим полем, что, естественно, скажется на электропроводности образца. Добавочный электрон имеет отрицательный (negative) заряд, и поэтому подобный полупроводник называется полупроводником n-типа. В терминах зонной теории этот процесс можно представить следующим образом. Локальный энергетический уровень этого электрона, связанный с наличием атома примеси, находится в запрещённой зоне недалеко от дна зоны проводимости (см. рис. 1). Достаточно небольшой порции энергии DЕД для того, чтобыэлектрон оторвался от такого атома (донора – от англ. donor – жертвователь, донор) и приобрёл энергию, соответствующую свободному электрону (перешёл с донорного уровня в зону проводимости: переход 2 на рис.1). Понятно, что это возможно, лишь если энергия DЕД не слишком велика (например, - сравнима с той, которая поставляется теплом). Если же примесные уровни размещаются далеко от дна зоны проводимости, то существенного влияния на электрические свойства кристалла они оказать не смогут. В германии n-типа тепловой энергии даже при обычных температурах оказывается достаточной для того, чтобы перевести все электроны с примесных уровней в зону проводимости. Это означает, что, если примеси достаточно, концентрация примесных электронов в зоне проводимости во много раз превысит концентрацию собственных, и данный полупроводник будет обладать примесной электронной проводимостью. Предположим теперь, что в решетке германия часть атомов Ge замещена атомами трехвалентного элемента, например, бора (B). Для образования связей с четырьмя ближайшими соседями у атома бора не хватает одного электрона. Поэтому одна из связей каждого из соседних атомов Ge оказывается неукомплектованной, способной захватить электрон. Данному состоянию соответствует уровень энергии, расположенный в запрещённой зоне вблизи потолка валентной зоны; состояние локализовано у атома бора. Уже при сравнительно небольшом тепловом возбуждении на этот уровень может быть захвачен электрон из валентной зоны (переход 3 на рис.1), при этом в валентной зоне возникнет вакантное энергетическое состояние - дырка, которая, как мы говорили ранее, может рассматриваться в качестве положительно заряженной квазичастицы, способной ускоряться электрическим полем. В то же время электрон, оказавшийся связанным с атомом германия, теряет возможность свободного перемещения по кристаллу. Таким образом, за протекание электрического тока в данном полупроводнике отвечают лишь дырки, поэтому его проводимость называют дырочной, а о полупроводнике говорят, что он принадлежит к p-типу (от слова positive - положительный). Примеси, захватывающие электроны из валентной зоны, называют акцепторами (от англ. to accept - принимать), а их энергетические уровни - акцепторными. Расстояние от потолка валентной зоны до уровня акцептора (точнее - разница соответствующих энергий) на рис. 1 обозначено как DЕА. Итак, наличие и характер примеси существенным образом влияют на электропроводность полупроводника: в собственном полупроводнике за неё ответственны как электроны, так и дырки, концентрации которых одинаковы, а в примесном (при не слишком высоких температурах) – только электроны (донорный полупроводник) или только дырки (акцепторный полупроводник). Температурная зависимость концентрации электронов n(T) в зоне проводимости донорного полупроводника (полагаем, что проводимость - электронная)определяется выражением
n(T)~ exp [ - DЕД /( 2 kT) ]; (5)
зависимость от температуры концентрации дырок p(T) в случае, если проводимость носит дырочный характер, описывается сходной формулой: p(T)~ exp [ - DЕА /( 2 kT) ]. (6)
Конечно же, электроны и дырки могут возникать парами и в примесном полупроводнике, подобно тому, как это происходит в полупроводнике собственном. Однако, при низких температурах концентрация таких носителей заряда много меньше концентрации электронов (или дырок), поставляемых атомами примесей; это следует, в частности, из формул (2), (5) и (6): Еg >> DЕД и Еg >> DЕА. Именно поэтому в полупроводниках n- и p-типа при низких температурах проводимость обусловлена главным образом примесными носителями – только электронами или только дырками. Удельная электропроводность донорного полупроводника в этом случае может быть вычислена, как sД = enun, а акцепторного – как sА = epup (сравните эти формулы с формулой(1)). Поскольку изменение температуры сказывается на подвижности u как электронов, так и дырок, значительно слабее, чем на их концентрации, то зависимость удельной электропроводности от температуры у примесных полупроводников при низких Т оказывается практически такой же, как и аналогичная зависимость концентрации носителей заряда (см. формулы (5) и (6)):
sД(T)~ exp [- DЕД /( 2 kT) ]; (7)
sА(T)~ exp [ - DЕА /( 2 kT) ]. (8)
Итак, в области низких температур, когда электронам хватает энергии лишь для переходов типа «уровень примеси - ближайшая зона», зависимость s(T) описывается одной из формул (7) или (8), причём сама проводимость носит примесный характер. С повышением температуры вероятность подобных переходов резко возрастает, и s растёт экспоненциальным образом. Введя обозначения y = ln [ s(T) ], x = 1/2 kТ, можно по результатам измерений s и T построить график зависимости y(x), которая также, как и зависимость (4), является линейной, после чего, определив тангенс угла наклона соответствующей прямой, - рассчитать величину DЕД (или DЕА). Рост электропроводности примесного полупроводника с увеличением температуры не является безграничным. По мере повышения T опустошается всё большее число донорных уровней и заполняется – акцепторных. По достижении некоторой температуры TS валентные электроны отдаст уже вся донорная примесь (или заполнятся все акцепторные уровни). В то же время, эта температура ещё слишком мала, чтобы вероятность переходов валентная зона – зона проводимости, ответственных за собственную проводимость, оказалась значительной. Это означает, что после достижения TS и вплоть до некоторой температуры Ti концентрация свободных носителей (электронов в зоне проводимости полупроводника n-типа и дырок в валентной зоне полупроводника p-типа) не меняется: очевидно, что на этом участке n = NД, где NД – концентрация атомов донорной примеси (константа), или p = NА, где NА – концентрация акцепторов (тоже константа). И хотя электропроводность s в этой области (которая носит название «область истощения примеси») всё же может меняться, так как здесь способна проявиться зависимость от температуры подвижности u (она может несколько возрастать, падать или меняться более сложным образом – см. книгу [1]), это изменение обычно невелико. При еще более высоких Т, когда резко возрастает вероятность электронных переходов зона - зона, проводимость становится собственной, и связь s с Т описывается уже соотношением (3). На рис. 2 изображен примерный график зависимости ln [ s(T) ] от 1/2 kТ для примесного полупроводника в широком интервале температур. В области низких Т (ему соответствует интервал а – б) мы имеем дело практически только с примесной проводимостью; наклон прямой, соответствующей этому участку графика, определяется энергией DЕД (или DЕА). При повышении температуры концентрация пр
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 2731; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.193.223 (0.015 с.) |

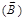 направляют перпендикулярно вектору плотности тока
направляют перпендикулярно вектору плотности тока  .
.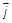 , так и к вектору индукции
, так и к вектору индукции 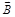 . В отсутствие магнитного поля точки А и А 1 лежат на эквипотенциальной поверхности.
. В отсутствие магнитного поля точки А и А 1 лежат на эквипотенциальной поверхности.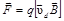 , (1)
, (1)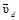 – средняя дрейфовая скорость.
– средняя дрейфовая скорость.
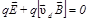 . (2)
. (2)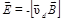 .
.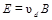 ,
, 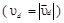 , что соответствует поперечной разности потенциалов:
, что соответствует поперечной разности потенциалов: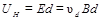 , (3)
, (3)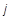 соотношением
соотношением 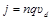 , где п –концентрация носителей заряда (число носителей в единице объема, q – заряд носителя). Следовательно,
, где п –концентрация носителей заряда (число носителей в единице объема, q – заряд носителя). Следовательно,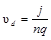 . (4)
. (4)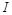 :
: , (5)
, (5) – толщина пластины) и подставив выражения (5) и (4) в (3), получим
– толщина пластины) и подставив выражения (5) и (4) в (3), получим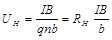 , (6)
, (6)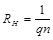 . (7)
. (7)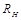 называют постоянной Холла.
называют постоянной Холла.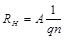 . (8)
. (8)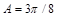 .
.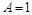 . В этом случае применима формула (7).
. В этом случае применима формула (7). , м-3 , в образце из опытных данных
, м-3 , в образце из опытных данных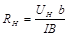 ;
; 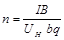 . (9)
. (9) и
и 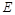 носители приобретают скорость
носители приобретают скорость 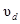 , то подвижность их
, то подвижность их  , м2/(В×с), равна
, м2/(В×с), равна . (10)
. (10) s
s  и учитывая (4) и (10), можно выразить подвижность через проводимость s и концентрацию носителей заряда:
и учитывая (4) и (10), можно выразить подвижность через проводимость s и концентрацию носителей заряда: . (11)
. (11)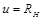 s. (12)
s. (12)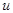 необходимо измерить
необходимо измерить  .
.
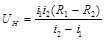 . (13)
. (13)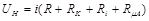 , (14)
, (14)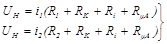 (15)
(15)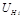 , B
(i= 1¸4)
, B
(i= 1¸4)
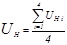 , B
, B
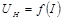 и определить по нему среднее значение отношения
и определить по нему среднее значение отношения  .
.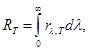 [Вт/м2], (1)
[Вт/м2], (1)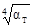 . (3)
. (3)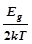 ,
,


