
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение температурной зависимостиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ЭЛЕКТРОПРОВОДНОСТИ ПОЛУПРОВОДНИКОВ Цель работы. Изучение температурной зависимости электропроводности полупроводников, определение ширины запрещенной зоны и энергии активации примесной проводимости.
Введение
Полупроводники - это широкий класс веществ, характеризующихся значениями удельной электропроводности s, промежуточными между удельной электропроводностью металлов: 106 ¸ 108 См/м* и диэлектриков: 10-10 ¸ 10-8 См/м (электропроводность указана при комнатной температуре). В отличие от металлов, электропроводность полупроводников увеличивается с ростом температуры и существенно зависит как от типа примесей, так и от их концентрации в образце. Соответственно различают собственную и примесную проводимость полупроводников.
Зона проводимости E Электроны проводимости
Уровень донорной примеси DEД 2 Еg – Ширина запрещённой зоны 1
Уровень акцепторной примеси DEА Валентная зона Дырки
Рис. 1
Рассмотрим механизм и особенности проводимости полупроводников, исходя из представлений зонной теории. Энергетические зоны полупроводника с собственной проводимостью (собственного полупроводника) при абсолютном нуле температуры изображены на рис.1. Над заполненной электронами валентной зоной располагается совершенно свободная зона проводимости. Валентная зона и зона проводимости разделены запрещенной зоной энергий, характеризующейся шириной Еg. В валентной зоне нет свободных энергетических состояний, а это означает, что электрическое поле не может придать электронам этой зоны добавочную кинетическую энергию и заставить их двигаться в определённом направлении: такой образец не проводит электрический ток и ведёт себя подобно диэлектрику. Собственная проводимость возникает под влиянием какого-либо внешнего воздействия (нагрева, облучения, сильного электрического поля), когда часть электронов с верхних уровней валентной зоны, оказывается способной перейти в зону проводимости (переходы 1 на рис. 1). Понятно, что для этого таким электронам нужно сообщить дополнительную энергию, равную, как минимум, ширине запрещенной зоны Еg данного полупроводника. Оказавшись в зоне проводимости, в которой очень много разрешенных уровней энергии, электроны уже могут ускоряться полем: при включении образца в электрическую цепь по нему начинает идти ток. У потолка валентной зоны после ухода электрона образуется вакантное энергетическое состояние. Это состояние может занять другой электрон валентной зоны, ускоренный электрическим полем до требуемой энергии. Но после этого окажется свободным его «старое» состояние, которое теперь сможет занять третий электрон, ускоренный полем, и т. д. Можно следить за поочерёдным переходом в освобождающиеся состояния (и о движении по кристаллу) одного электрона за другим, а можно говорить о миграции по кристаллу свободного энергетического состояния. Вакантное энергетическое состояние в валентной зоне называется дыркой; его удобно рассматривать как движущуюся по кристаллу квазичастицу, имеющую такой же по величине заряд, как у электрона, но противоположный ему по знаку (положительный). Таким образом, в создании собственной электропроводимости полупроводников участвуют два вида носителей заряда - электроны и дырки. Величина удельной электропроводности s собственного полупроводника зависит от их концентрации п (числа в единице объема) и подвижности u, под которой понимается средняя дрейфовая скорость, приобретаемая электронами и дырками в электрическом поле единичной напряженности. Очевидно, что в собственном полупроводнике концентрация дырок равна концентрации электронов в зоне проводимости, и собственная электропроводность полупроводника s = en(un+ up),(1)
где e - заряд электрона; un и up - подвижности электронов и дырок соответственно. При увеличении температуры число электронов, способных перейти запрещенную зону, увеличивается, и поэтому их концентрация в зоне проводимости собственного полупроводника возрастает: n ~ exp [ - Еg /( 2 kT) ], (2) где Еg – ширина запрещенной зоны; k = 1,38×10-23 Дж/К – постоянная Больцмана, T – абсолютная температура. Подвижность носителей заряда зависит от температуры значительно слабее, чем их концентрация. Вследствие этого зависимость s(T) собственного полупроводника определяется зависимостью п(Т ) и является экспоненциальной: s(T) = s0C ×exp [ - Еg /( 2 kT) ], (3) где s0C - слабо зависящий от температуры множитель. Из формулы (3) следует, что логарифм удельной электропроводности ln [ s(T) ] является линейной функцией от 1/2 kТ: ln [ s(T) ] = ln [ s0C ]- или, введя обозначения y = ln [ s(T) ], x = 1/2 kТ и a = ln [ s0C ]: y = a - Еg×x. (4)
Графиком зависимости y(x) является прямая; это означает, что ширину запрещенной зоны можно вычислить, определив тангенс угла наклона данной прямой к оси абсцисс. До сих пор мы говорили о собственной проводимости полупроводника, однако, введение в него примеси может существенным образом сказаться на его электрических свойствах. Для выяснения механизма примесной проводимости рассмотрим, что происходит при введении атомов из пятой и третьей групп таблицы Менделеева в германий - элемент четвёртой группы. На внешней электронной орбите атомы германия (Ge) имеют по четыре валентных электрона; при объединении атомов в кристаллическую решётку возникают ковалентные связи: электроны внешних орбит у соседних атомов попарно обобществляются. Но если в такую решётку ввести примесный атом с валентностью, равной пяти, например, фосфор (P), мышьяк (As) или сурьму (Sb), то, заняв в ней место одного из основных атомов и отдав четыре электрона соседям, такой атом всё равно будет иметь один «лишний» электрон, который способен оторваться от «хозяина» и свободно перемещаться по кристаллу германия. В частности, он может ускоряться электрическим полем, что, естественно, скажется на электропроводности образца. Добавочный электрон имеет отрицательный (negative) заряд, и поэтому подобный полупроводник называется полупроводником n-типа. В терминах зонной теории этот процесс можно представить следующим образом. Локальный энергетический уровень этого электрона, связанный с наличием атома примеси, находится в запрещённой зоне недалеко от дна зоны проводимости (см. рис. 1). Достаточно небольшой порции энергии DЕД для того, чтобыэлектрон оторвался от такого атома (донора – от англ. donor – жертвователь, донор) и приобрёл энергию, соответствующую свободному электрону (перешёл с донорного уровня в зону проводимости: переход 2 на рис.1). Понятно, что это возможно, лишь если энергия DЕД не слишком велика (например, - сравнима с той, которая поставляется теплом). Если же примесные уровни размещаются далеко от дна зоны проводимости, то существенного влияния на электрические свойства кристалла они оказать не смогут. В германии n-типа тепловой энергии даже при обычных температурах оказывается достаточной для того, чтобы перевести все электроны с примесных уровней в зону проводимости. Это означает, что, если примеси достаточно, концентрация примесных электронов в зоне проводимости во много раз превысит концентрацию собственных, и данный полупроводник будет обладать примесной электронной проводимостью. Предположим теперь, что в решетке германия часть атомов Ge замещена атомами трехвалентного элемента, например, бора (B). Для образования связей с четырьмя ближайшими соседями у атома бора не хватает одного электрона. Поэтому одна из связей каждого из соседних атомов Ge оказывается неукомплектованной, способной захватить электрон. Данному состоянию соответствует уровень энергии, расположенный в запрещённой зоне вблизи потолка валентной зоны; состояние локализовано у атома бора. Уже при сравнительно небольшом тепловом возбуждении на этот уровень может быть захвачен электрон из валентной зоны (переход 3 на рис.1), при этом в валентной зоне возникнет вакантное энергетическое состояние - дырка, которая, как мы говорили ранее, может рассматриваться в качестве положительно заряженной квазичастицы, способной ускоряться электрическим полем. В то же время электрон, оказавшийся связанным с атомом германия, теряет возможность свободного перемещения по кристаллу. Таким образом, за протекание электрического тока в данном полупроводнике отвечают лишь дырки, поэтому его проводимость называют дырочной, а о полупроводнике говорят, что он принадлежит к p-типу (от слова positive - положительный). Примеси, захватывающие электроны из валентной зоны, называют акцепторами (от англ. to accept - принимать), а их энергетические уровни - акцепторными. Расстояние от потолка валентной зоны до уровня акцептора (точнее - разница соответствующих энергий) на рис. 1 обозначено как DЕА. Итак, наличие и характер примеси существенным образом влияют на электропроводность полупроводника: в собственном полупроводнике за неё ответственны как электроны, так и дырки, концентрации которых одинаковы, а в примесном (при не слишком высоких температурах) – только электроны (донорный полупроводник) или только дырки (акцепторный полупроводник). Температурная зависимость концентрации электронов n(T) в зоне проводимости донорного полупроводника (полагаем, что проводимость - электронная)определяется выражением
n(T)~ exp [ - DЕД /( 2 kT) ]; (5)
зависимость от температуры концентрации дырок p(T) в случае, если проводимость носит дырочный характер, описывается сходной формулой: p(T)~ exp [ - DЕА /( 2 kT) ]. (6)
Конечно же, электроны и дырки могут возникать парами и в примесном полупроводнике, подобно тому, как это происходит в полупроводнике собственном. Однако, при низких температурах концентрация таких носителей заряда много меньше концентрации электронов (или дырок), поставляемых атомами примесей; это следует, в частности, из формул (2), (5) и (6): Еg >> DЕД и Еg >> DЕА. Именно поэтому в полупроводниках n- и p-типа при низких температурах проводимость обусловлена главным образом примесными носителями – только электронами или только дырками. Удельная электропроводность донорного полупроводника в этом случае может быть вычислена, как sД = enun, а акцепторного – как sА = epup (сравните эти формулы с формулой(1)). Поскольку изменение температуры сказывается на подвижности u как электронов, так и дырок, значительно слабее, чем на их концентрации, то зависимость удельной электропроводности от температуры у примесных полупроводников при низких Т оказывается практически такой же, как и аналогичная зависимость концентрации носителей заряда (см. формулы (5) и (6)):
sД(T)~ exp [- DЕД /( 2 kT) ]; (7)
sА(T)~ exp [ - DЕА /( 2 kT) ]. (8)
Итак, в области низких температур, когда электронам хватает энергии лишь для переходов типа «уровень примеси - ближайшая зона», зависимость s(T) описывается одной из формул (7) или (8), причём сама проводимость носит примесный характер. С повышением температуры вероятность подобных переходов резко возрастает, и s растёт экспоненциальным образом. Введя обозначения y = ln [ s(T) ], x = 1/2 kТ, можно по результатам измерений s и T построить график зависимости y(x), которая также, как и зависимость (4), является линейной, после чего, определив тангенс угла наклона соответствующей прямой, - рассчитать величину DЕД (или DЕА). Рост электропроводности примесного полупроводника с увеличением температуры не является безграничным. По мере повышения T опустошается всё большее число донорных уровней и заполняется – акцепторных. По достижении некоторой температуры TS валентные электроны отдаст уже вся донорная примесь (или заполнятся все акцепторные уровни). В то же время, эта температура ещё слишком мала, чтобы вероятность переходов валентная зона – зона проводимости, ответственных за собственную проводимость, оказалась значительной. Это означает, что после достижения TS и вплоть до некоторой температуры Ti концентрация свободных носителей (электронов в зоне проводимости полупроводника n-типа и дырок в валентной зоне полупроводника p-типа) не меняется: очевидно, что на этом участке n = NД, где NД – концентрация атомов донорной примеси (константа), или p = NА, где NА – концентрация акцепторов (тоже константа). И хотя электропроводность s в этой области (которая носит название «область истощения примеси») всё же может меняться, так как здесь способна проявиться зависимость от температуры подвижности u (она может несколько возрастать, падать или меняться более сложным образом – см. книгу [1]), это изменение обычно невелико. При еще более высоких Т, когда резко возрастает вероятность электронных переходов зона - зона, проводимость становится собственной, и связь s с Т описывается уже соотношением (3). На рис. 2 изображен примерный график зависимости ln [ s(T) ] от 1/2 kТ для примесного полупроводника в широком интервале температур. В области низких Т (ему соответствует интервал а – б) мы имеем дело практически только с примесной проводимостью; наклон прямой, соответствующей этому участку графика, определяется энергией DЕД (или DЕА). При повышении температуры концентрация примесных носителей достигает насыщения (интервал б – в), в результате чего ход графика определяется уже только зависимостью u(T). На рис. 2 интервал б – в соответствует случаю уменьшения подвижности (а следовательно, и s)с ростом температуры. Наконец, на участке в – г температура уже настолько высока, что начинается очень быстрое увеличение числа собственных электронов и дырок, и мы вступаем в область собственной проводимости. Наклон прямой, соответствующей этому участку графика, определяется шириной запрещенной зоны Еg. Кривая, представленная на рис. 2, выражает в весьма схематичной форме общие закономерности изменения проводимости полупроводников с температурой. У реальных полупроводников эта зависимость может оказаться сложнее. Заметим также, что довольно часто области примесной проводимости соответствуют температуры существенно ниже комнатной: так, например, для германия (Еg = 0,72 эВ), легированного донорной примесью с NД = 1022 м-3 и DЕД = 0,01 эВ, температура, при которой начинается истощение примеси, TS = 32 К, а температура, соответствующая началу области собственной проводимости, Ti = 450 К.
Сильная зависимость электропроводности полупроводников от температуры используется для создания разнообразных приборов, позволяющих с большой точностью измерять температуру, регулировать скорость возрастания тока, стабилизировать напряжение в электрических цепях, измерять на расстоянии мощность источников электромагнитного излучения и т. д. Для нас важно, что измерив значения электропроводности полупроводника при разных температурах и построив соответствующий график, можно определить энергетическое параметры самого полупроводника – ширину его запрещённой зоны Е g и глубину залегания примесных уровней DЕД (или DЕА ). Описание аппаратуры и методика измерений
Приборы и принадлежности: полупроводниковая пластина; миллиамперметр; источник напряжения, подаваемого на образец; термопара; милливольтметр; источник питания нагревателя; нагреватель. Данная работа связана с измерением температурной зависимости электропроводности полупроводникового образца, имеющего форму пластины, расположенной на изолирующей подложке. С помощью двух прижимных контактов на образец подается электрическое напряжение от стабилизированного источника; возникающий при этом ток через пластину регистрируется с помощью миллиамперметра. Непосредственно под образцом располагается нагреватель: после подключения нагревателя к источнику питания температура образца начинает повышаться. Измерения температуры проводятся при помощи термопары; возникающая термоЭДС регистрируется милливольтметром. Принципиальная схема установки изображена на рис. 3.
mV Прижимные контакты Термопара Образец
Подложка Нагреватель Источник напряжения Источник питания нагревателя Рис. 3
Рассмотрим, как в настоящей работе определяются основные энергетические характеристики полупроводника. Согласно закону Ома, I = U/R, (9) где U - напряжение на проводнике, I – сила тока через проводник, R – коэффициент, который называется сопротивлением. Величина этого коэффициента зависит от свойств и формы проводника, от его температуры. Известно, в частности, что для длинного прямого проводника R = r где l - длина проводника, S - площадь его поперечного сечения, r - его удельное сопротивление, причём r = s -1. Таким образом, можно записать: I = SUs/l. (11) Полагая, что с изменением температуры геометрические размеры образца (l и S) меняются мало, можно считать, что при заданном напряжении зависимость от температуры силы тока I(T) через образец полностью определяется температурной зависимостью его удельной электропроводности:
I (T) ~ s(T). (12)
Таким образом, измерение зависимости I от Т в достаточно широком температурном диапазоне позволяет определить как ширину запрещенной зоны полупроводника Еg, так и глубину залегания примесных уровней DЕД (или DЕА). Сравнивая полученные данные с табличными, можно определить, из какого материала изготовлен исследуемый образец. Сам образец (рис. 3) вмонтирован в один блок с электрическим нагревателем. Миллиамперметр, регистрирующий ток через образец, расположен на лицевой панели установки; на стенде также установлен милливольтметр для измерения термоЭДС. Градуировочный график, позволяющий переводить показания милливольтметра в градусы Цельсия, укреплен на установке. Для повышения точности эксперимента данные измерений снимаются два раза: при нагреве и при остывании образца. Нагреватель включается и выключается при помощи тумблера, укрепленного на передней панели установки.
Порядок выполнения работы 1. Ознакомьтесь со схемой, изображенной на рис. 3, и, пользуясь этой схемой, определите, где на стенде располагаются соответствующие приборы, а также - какова цена их деления. 2. Ознакомьтесь с градуировочным графиком термопары, используемой в установке (график размещен на лабораторном стенде). 3. Включите источник напряжения (УСИП), подаваемого на образец. Установив напряжение на выходе УСИП равным 6 В, по показаниям миллиамперметра проверьте, идет ли в цепи электрический ток. 4. Включите блок питания нагревателя (ВУП-2) и по мере повышения температуры (начиная от комнатной до +70°С) через каждые 5°С фиксируйте силу тока I+, проходящего по образцу. Результаты измерений запишите в таблицу 1.
Таблица 1
5. Выключите блок питания нагревателя и по мере остывания образца через каждые 5°С фиксируйте силу тока I-, проходящего по образцу. Результаты измерений запишите в таблицу 1. 6. Для каждой температуры вычислите среднее (при нагреве и остывании) значение силы тока I через образец. Используя формулу (11), рассчитайте величину удельной электропроводности s образца для разных температур. Значения l и S представлены на стенде. Результаты вычислений занесите в таблицу 1. При расчётах учесть, что 1 эВ = 1,6×10-19Дж. Постройте график зависимости ln [ s(T) ] от 1/2 kТ. Пользуясь графиком, определите основные энергетические параметры полупроводника: Е g, и DЕД (или DЕА ); выразите их в электронвольтах. Пользуясь таблицами 2 и 3, определите, из какого материала изготовлен исследуемый образец.
Таблица 2 Значения ширины запрещённой зоны некоторых кристаллов
Таблица 3 Глубина залегания некоторых примесных уровней в германии и кремнии
8. Используя данные о концентрации примеси в полупроводнике (данные размещены на стенде), оцените величину подвижности носителей заряда в нём. При расчете учтите, что в области истощения примеси на графике ln [ s(T) ] от 1/2 kТ концентрация электронов в полупроводнике равна концентрации примеси. Для вычислений используйте формулы (1) и (11). КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Чем полупроводник отличается от металла? От диэлектрика? Начертите зонные схемы металла, полупроводника и диэлектрика. При подготовке к ответу на этот вопрос используйте книгу [1]. 2. Что называется собственной и примесной проводимостью полупроводников? Ответ поясните, используя зонную схему. 3. Что такое донорные и акцепторные примеси? Приведите пример, атомы каких элементов нужно ввести в германий с тем, чтобы получить полупроводник p- и n-типа. 4. Объясните, почему электропроводность полупроводников зависит от температуры. Какие участки на зависимости удельной электропроводности от температуры можно выделить, и чем обусловлено их наличие? 5. Как, пользуясь графиком зависимости удельной электропроводности примесного полупроводника от температуры, можно определить ширину его запрещенной зоны и глубину залегания примесных уровней энергии? Ответ поясните соответствующими формулами.
СПИСОК ЛИТЕРАТУРЫ
1. Физика твёрдого тела: Учебное пособие для технических университетов / И.К.Верещагин, С.М.Кокин, В.А.Никитенко, В.А.Селезнёв, Е.А.Серов; Под ред. И.К.Верещагина. - М.: Высшая школа, 2001. - 237 с. 2. Савельев И.В. Курс общей физики, т. 3. М.: Наука, 1987, - 320 с.
РАБОТА 52
ИЗУЧЕНИЕ РАБОТЫ ОПТИЧЕСКОГО КВАНТОВОГО ГЕНЕРАТОРА (ЛАЗЕРА)
Цель работы. Ознакомление с устройством и работой лазера, исследование его характеристик.
Введение Принцип работы оптического квантового генератора как источника когерентного света связан с особым возбужденным состоянием излучающей среды. Частицы среды (атомы, молекулы, ионы) могут находиться в различных состояниях, которым соответствуют определенные значения энергии. Состояние с наименьшей энергией называют основным состоянием, остальные состояния носят название возбужденных состояний. Сообщая системе частиц энергию, можно перевести частицы из основного состояния, в котором преимущественно они находятся при нормальных условиях, в возбужденное. Однако, время пребывания частиц в данном возбужденном состоянии (время жизни состояния) ограничено. Переходя в более низкое энергетическое состояние, частицы отдают энергию. В частности, эта энергия может отдаваться в виде квантов света (фотонов). Такой процесс излучения называется спонтанным (самопроизвольным) и он происходит в обычных некогерентных источниках света. Источником когерентного излучения называется источник, испускающий электромагнитную волну, в которой имеется согласованность между фазами колебаний в различных точках пространства в один и тот же момент времени (пространственная когерентность) или между фазами колебаний в одной и той же точке пространства в различные моменты времени (временная когерентность). Две волны будут называться когерентными, если их частоты совпадают и волны имеют постоянную разность фаз во времени. В обычных источниках света частицы излучают спонтанно, независимо друг от друга. Испускаемые частицами волновые цуги, представляющие собой непрерывную последовательность максимумов и минимумов колебаний, не согласованы друг с другом во времени и имеют длительность порядка t Однако, частицы, находящиеся в возбужденных состояниях, могут под действием внешней электромагнитной волны, имеющей частоту, равную частоте спонтанного излучения этих частиц, испускать вторичные волны, у которых частота, поляризация, направление распространения и фаза полностью совпадают с характеристиками внешней волны. Таким образом, получается усиление первичной волны и связь между собой всех волновых цугов, испускаемых частицами, то есть результирующая волна является когерентной во времени и в пространстве. Такое излучение называется вынужденным и осуществляется в лазерах. В настоящий момент удалось создать источники вынужденного излучения на основе многих веществ, находящихся в различных агрегатных состояниях. Таким образом, при прохождении электромагнитной волны через систему частиц, находящихся в возбужденном состоянии, возможно получение вынужденного излучения. Однако, в то же самое время возможен процесс поглощения данной электромагнитной волны частицами, находящимися в основном состоянии. И будет ли система частиц преимущественно испускать свет или поглощать зависит от того, сколько частиц находится в возбужденном и невозбужденном состояниях. Число частиц в единице объема среды, пребывающих в состояниях, которым соответствует определенный энергетический уровень, называется населенностью этого уровня. Для возникновения вынужденного излучения необходимо, чтобы населенность любого возбужденного уровня была больше, чем населенность нижележащего уровня. Такая система называется системой с инверсией населенности. Фотон с энергией, равной разности энергий возбужденного и невозбужденного уровней (это может быть и спонтанно испущенный системой фотон), способен вызвать вынужденное излучение какой-либо из возбужденных частиц среды. Возникшее вынужденное излучение управляет дальнейшим процессом испускания света другими возбужденными частицами. Для обеспечения непрерывности данного процесса необходимо, чтобы часть энергии вынужденного излучения оставалась внутри системы. Это осуществляется с помощью резонатора. Резонатор представляет собой два зеркала, одно из которых (иногда оба) полупрозрачно. Между зеркалами помещается излучающее вещество. Часть излучения выводится вовне через полупрозрачное зеркало, а часть возвращается обратно и, проходя через вещество, управляет дальнейшим процессом излучения, одновременно усиливаясь. Однако для получения незатухающего излучения необходимо, чтобы усиление за один проход всего резонатора было бы больше, чем потери за счет рассеяния и вывода вовне части излучения через полупрозрачное зеркало. Из этого условия следует, что усиление будет происходить главным образом для пучков, проходящих через всю возбужденную среду, т.е. для пучков, распространяющихся вдоль оси резонатора. Иначе говоря, излучение лазера будет строго направленным.
На рис. 1 представлена схема лазера, когда излучающим телом является газ в стеклянной трубке-капилляре (газоразрядная трубка) 3 с впаянными электродами 4. Резонатор составлен отражающим 1 и полупрозрачным 5 зеркалами. Выходные окошки 2 трубки расположены под некоторым углом к оси трубки. Итак, излучение лазера является монохроматическим, направленным, поляризованным и когерентным. Однако надо заметить, что строгой когерентности и монохроматичности достичь не удается. Например, лучшей временной когерентностью (наибольшей длительностью t цугов волн) обладают газовые лазеры: t В заключение надо отметить, что благодаря своим уникальным характеристикам (когерентность, направленность и монохроматичность излучения, возможность получения мощных пучков) лазеры находят широкое применение как в научных исследованиях, так и в таких областях как металлургия, медицина, связь, кибернетика, космонавтика, военная техника и др.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.118 (0.013 с.) |


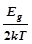 ,
,

 , (10)
, (10)
 с. Если рассматривать волны от разных точек такого источника, то они окажутся некогерентными.
с. Если рассматривать волны от разных точек такого источника, то они окажутся некогерентными.
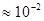 с. Не удается получить и строгой направленности пучка, прежде всего – из-за дифракции на выходном отверстии лазера (равном диаметру выходящего пучка). Кроме того, направленность ухудшается из-за образования сложных типов волн в резонаторе, называемых модами колебаний. Различные моды колебаний имеют разную угловую расходимость.
с. Не удается получить и строгой направленности пучка, прежде всего – из-за дифракции на выходном отверстии лазера (равном диаметру выходящего пучка). Кроме того, направленность ухудшается из-за образования сложных типов волн в резонаторе, называемых модами колебаний. Различные моды колебаний имеют разную угловую расходимость.


