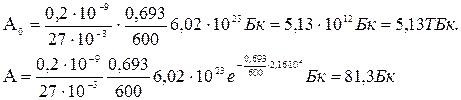Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
частицы, вызывающей ядерную реакциюСодержание книги
Поиск на нашем сайте
где частицы,
Примеры решения задач. Пример 45. Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Определить энергию испущенного при этом фотона. Решение. Для определения энергии фотона воспользуемся формулой для водородоподобных ионов:
где λ – длина волны; R – постоянная Ридберга; Z – заряд ядра в относительных единицах (при Z=1 формула переходит в серийную формулу для водорода); n1 – номер орбиты, на которую перешел электрон;n2 – номер орбиты, с которой перешел электрон (n1 и n2 - главные квантовые числа). Энергия фотона ε выражается формулой
Поэтому, умножив обе части равенства (1) на hc, получим выражение для энергии фотона
Так как Rhc есть энергия ионизации Еi атома водорода, то
Вычисление выполним во внесистемных единицах: Еi =13,6 эВ; Z=1; n1=2; n2=4:
Пример 46. При соударении α-частицы с ядром бора Решение. Обозначим неизвестное ядро символом
Применив закон сохранения числа нуклонов, получим уравнение 4+10= 1 +А, откуда А = 13. Применив закон сохранения заряда, получим уравнение 2 + 5 = 1+Z, откуда Z = 6. Следовательно, неизвестное ядро является ядром атома изотопа углерода Теперь можем записать реакцию в окончательном виде:
Энергетический эффект Q ядерной реакции определяется по формуле Q=931[(mHe + mB)-(mH + mC)]. Здесь в первых круглых скобках указаны массы исходных ядер, во вторых скобках — массы ядер — продуктов реакции. При числовых подсчетах по этой формуле массы ядер заменяют массами нейтральных атомов. Возможность такой замены вытекает из следующих соображений. Число электронов в электронной оболочке нейтрального атома равно его зарядовому числу Z. Сумма зарядовых чисел исходных ядер равна сумме зарядовых чисел ядер — продуктов реакции. Следовательно, электронные оболочки ядер гелия и бора содержат вместе столько же электронов, сколько их содержат электронные оболочки ядер углерода и водорода. Очевидно, что при вычитании суммы масс нейтральных атомов углерода и водорода из суммы масс атомов гелия и бора массы электронов выпадут, и мы получим тот же результат, как если бы брали массы ядер. Подставив массы атомов (см. табл. 10 Приложения) в расчетную формулу, получим Q=931(4,00260+10,01294)-(1,00783+13,00335) МэВ = = 4,06 МэВ. Пример 47. Вычислить дефект массы и энергию связи ядра Решение. Масса ядра всегда меньше суммы масс свободных (находящая вне ядра) протонов и нейтронов, из которых ядро образовалось. Дефект массы ядра Δm и есть разность между суммой масс свободных нуклонов (протонов и нейтронов) и массой ядра, т. е. Δm =Zmp+(A-Z)mn-mя (1) где Z — атомный номер (число протонов в ядре); А — массовое число (число нуклонов, составляющих ядро); mр, mn, mя — соответственно массы протона, нейтрона и ядра. В справочных таблицах всегда даются массы нейтральных атомов, но не ядер, поэтому формулу (1) целесообразно преобразовать так, чтобы в нее входила масса mянейтрального атома. Можно считать, что масса нейтрального атома равна сумме масс ядра и электронов, составляющих электронную оболочку атома: mа=mя + Zme, откуда Mя=mа – Zme (2) Выразив в равенстве (1) массу ядра по формуле (2), получаем Δm =Zmp+(A-Z)mn- mа + Zme, или Δm=Z(mp +me)+(А –Z) mn - mа Замечая, что mр-mе = mн, где mн - масса водорода, окончательно находим Δm=Zmн+(А-Z) mn - mа . (3)
Подставив в выражение (3) числовые значения масс (см. табл. 12 и 13 Приложения), получим Δm = [3·1,00783+(7-3) · 1,00867-7·0,1601] а. е. м =0,04216 а.е. м. В соответствии с законом пропорциональности массы и энергии Е =Δ тс2,(4) где с - скорость света в вакууме. Коэффициент пропорциональности с2 может быть выражен двояко: с2= 9·1016 м2/с2, или с2 =ΔЕ/ Δm=9·1016Дж/кг Если вычислить энергию связи, пользуясь внесистемными единицами, то с2 = 931 МэВ/а. е. м. С учетом этого формула (4) примет вид Е=931Δm(МэВ). (5) Подставив найденное значение дефекта массы ядра в формулу (5), получим Е = 93 1 • 0,042 1 6 МэВ = 39,2 МэВ. Примечание. Термин «дефект массы» часто применяют в другом смысле: дефектом массы Δm называют разность между массой нейтрального атома данного изотопа и его массовым числом А: Δ = mа — А. Эта величина особого физического смысла не имеет, но ее использование позволяет в ряде случаев значительно упростить вычисления. В настоящем пособии всюду имеется в виду дефект массы Δmα, определяемый формулой (1).
Пример 48. Определить начальную активность А0 радиоактивного препарата магния Решение. Активность А изотопа характеризует скорость радиоактивного распада и определяется отношением числа dN ядер, распавшихся за интервал времени dt, к этому интервалу:
Знак «-» показывает, что число N радиоактивных ядер с течением вр6емени убывает. Для того чтобы найти
где N- число радиоактивных ядер, содержащихся в изотопе, в момент времени t; N0- число радиоактивных ядер в момент времени, принятый за начальный (t=0);λ- постоянная радиоактивного распада. Продифференцируем выражение (2) по времени:
Исключим из формул (1) и (2) dN/dt, находим активность препарата в момент времени t:
Начальную активность А0 препарата получим при t=0:
Постоянная полураспада λ связана с периодом полураспада Т1/2 соотношением
Число N0 радиоактивных ядер, содержащихся в изотопе, равно произведению постоянной Авогадро NА на количество вещества ν Данного изотопа:
где m- масса изотопа; М- молярная масса. С учетом выражений (6) и (7) формулы (5) и (4) принимают вид
Произведем вычисления, учитывая, что Т1/2=600с (см табл. 13 Приложения), ln2=0,693; t=6 ч = 2,16·104с:
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.92 (0.006 с.) |

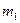 - масса покоя налетающей
- масса покоя налетающей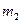 - масса покоящейся частицы,
- масса покоящейся частицы,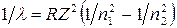 , (1)
, (1) , (2)
, (2)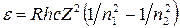 .
.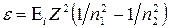 .
.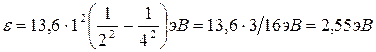
 произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода
произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода  Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции и определить ее энергетический эффект.
Определить порядковый номер и массовое число второго ядра, дать символическую запись ядерной реакции и определить ее энергетический эффект.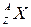 . Так как α-частица представляет собой ядро гелия
. Так как α-частица представляет собой ядро гелия  , запись реакции имеет вид
, запись реакции имеет вид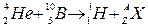
 .
.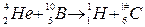

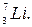
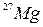 массой m=0,2 мкг, а также его активность А через время t=6 ч. Период полураспада
массой m=0,2 мкг, а также его активность А через время t=6 ч. Период полураспада  магния считать известным.
магния считать известным.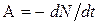 (1)
(1)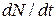 , воспользуемся законом радиоактивного распада:
, воспользуемся законом радиоактивного распада: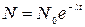 , (2)
, (2)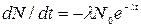 (3).
(3).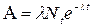 (4)
(4)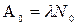 (5)
(5)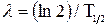 (6)
(6)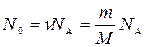 , (7)
, (7)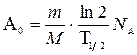 (8),
(8),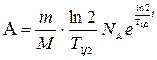 (9).
(9).