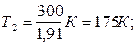Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь между линейными и угловымиСодержание книги
Поиск на нашем сайте
величинами Импульс (количество движения) материальной точки где m-масса материальной точки Основное уравнение динамики материальной точки (второй закон Ньютона) Закон сохранения импульса для изолированной системы Радиус-вектор центра масс Сорость частиц после столкновения упругого центрального где
Сила сухого трения где f -коэффициент трения;
Сила упругости где k-коэффициент упругости (жесткость);
Сила гравитационного взаимодействия где G-гравитационная постоянная; r- расстояние между частицами. Работа силы Мощность Потенциальная энергия Упругодеформированного тела гравитационного взаимодействия двух частиц тела в однородном гравитационном поле где g -напряженность гравитационного поля (ускорение свободного падения); h- расстояние от нулевого уровня. Напряженность гравитационного поля Земли где
h- расстояние от поверхности Земли. Потенциал гравитационного поля Земли Кинетическая энергия материальной Точки Закон сохранение механической энергии Момент инерции материальной точки где r -расстояние до оси вращения
Момент инерции тел массой m относительно Оси, проходящей через центр масс тонкостенного цилиндра (кольца) радиуса R, если ось вращения совпадает с осью цилиндра сплошного цилиндра (диска) радиуса R, если ось вращения совпадает с осью цилиндра шара радиуса R тонкого стержня длинной l, если ось вращения перпендикулярна стержню Момент инерции тела массой m относительно произвольной оси (теорема Штейнера) где параллельной оси, проходящей через центр масс; d -расстояние между осями. Момент силы где r -радиус-вектор точки приложения силы Момент импульса Основное уравнение динамики вращательного движения Закон сохранения момента импульса для изолированной системы Работа при вращательном движении Кинетическая энергия вращающегося тела Количество вещества где N –число молекул;
m- масса вещества; М -молярная масса. Уравнение Клапейрона-Менделеева pV=vRT, где p -давление газа; V -его объем; R -молярная газовая постоянная; T -термодинамическая температура. Уравнение молекулярно-кинетической теории газов где n-концентрация молекул,
поступательного движения молекул;
Средняя энергия молекулы где i - число степеней свободы; k -постоянная Больцмана Внутренняя энергия идеального газа Скорости молекул: средняя квадратичная средняя арифметическая наиболее вероятная Средняя длина свободного пробега молекулы где d -эффективный диаметр молекулы Среднее число столкновений молекул в единицу времени Распределение молекул в потенциальном поле сил где П- потенциальная энергия молекулы. Барометрическая формула Уравнение диффузии где D -коэффициент диффузии;
dS -элементарна площадка, перпендикулярная оси Ox. Уравнение теплопроводности где H -теплопроводность Сила внутреннего трения где Коэффициент диффузии Вязкость (динамическая) Теплопроводность где Молярная теплоемкость идеального газа изохорная изобарная Первое начало термодинамики
Работа расширения газа при процессе изобарном изотермическом адиабатном где Уравнение Пуассона
КПД цикла Карно где Q и T- количество теплоты, полученное от нагревателя и его температура;
холодильнику, и его температура.
Примеры решения задач Пример 1. Уравнение движения материальной точки вдоль оси имеет вид х = А+В+Сt Решение. Координату х найдем, подставив в уравнение движения числовые значения коэффициентов А, В и С и времени t:
Мгновенная скорость есть первая производная от координаты по времени:
Ускорение точки найдем, взяв первую производную от скорости по времени:
В момент времени t = 2 c:
Пример 2. Тело вращается вокруг неподвижной оси по закону φ = А+Bt+Ct2 t = 4 c. Решение. Полное ускорение в точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения аτ, направленного по касательной к траектории, и нормального ускорения аπ, направленного к центру кривизны траектории (рис. 1):
Так как векторы аτ и аπ взаимно перпендикулярны, то модуль ускорения равен:
где ω – угловая скорость тела; ε – его угловое ускорение. Подставляя выражения аτ и аπ в формулу (1), находим:
Угловую скорость ω найдем, взяв первую производную угла поворота по времени:
В момент времени t = 4 с угловая скорость равна: ω=[20+2(-2)4]рад/с =4 рад/с. ε=dω/dt=2C=-4рад/с. Подставляя значения ω, ε и r в формулу (3), получаем:
Пример 3. При выстреле из пружинного пистолета вертикально вверх пуля массой m=20 г поднялась на высоту h=5 м. Определить жесткость k пружины пистолета, если она была сжата на х=10 см. Массой пружины пренебречь. Решение. Система пуля – Земля (вместе с пистолетом) является замкнутой системой, в которой действуют консервативные силы: силы упругости и силы тяготения. Поэтому для решения задачи можно применить закон сохранения энергии в механике. Согласно ему полная механическая энергия Е1=Е2 или Т1+П1=Т2+П2 (1) где Т1,Т2,П1 и П2 - кинетические и потенциальные энергии системы в начальном и конечном состояниях. Так как кинетические энергии пули в начальном и конечном состояниях равны нулю, то (1) примет вид
Если потенциальную энергию в поле сил тяготения Земли на ее поверхности принять равной нулю, то энергия системы в начальном состоянии будет равна потенциальной энергии сжатой пружины, т.е.
Подставив выражения
Проверим, дает ли полученная формула единицу жесткости k. Для этого в правую часть формулы (3) вместо величин, подставим их единицы:
Пример 4. Шар массой m1, движущийся горизонтально с некоторой скоростью υ1, столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю ε своей кинетической энергии первый шар передал второму? Решение. Доля энергии, переданной первым шаром второму, выразится соотношением:
где T1 - кинетическая энергия первого шара до удара; u2 и T2 – скорость и кинетическая энергия второго шара после удара. Как видно из формулы (1), для определения ε надо найти u2. При ударе абсолютно упругих тел одновременно выполняются законы сохранения импульса и механической энергии. Пользуясь этими законами, найдем:
Решим совместно уравнения (2) и (3):
Подставим это выражение для и2 в формулу (1), сократив на
Из найденного соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров. Доля передаваемой энергии не изменится, если шары поменять местами. Пример 5. Через блок в виде сплошного диска, имеющего массу т = 80 г (рис. 2), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами т1 =100г и т2 =200 г. Определить ускорение, с которым будут двигаться грузы, если их Решение. Воспользуемся основными уравнениями динамики поступательного и вращательного движений. Для этого рассмотрим силы, действующие на каждый груз в отдельности и на блок. На первый груз действуют две силы: сила тяжести т1g и сила упругости (сила натяжения нити) Т1. Спроецируем эти силы на ось Х, которую направим вертикально вниз, и напишем уравнение движения (второй закон Ньютона):
Уравнение движения для второго груза: т2g - Т2 =т2а Под действием двух моментов сил T1r и T2r относительно оси, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение ε. Согласно основному уравнению динамики вращательного движения
где ε = а/r;
Согласно третьему закону Ньютона
После сокращения на r и перегруппировки членов найдем:
Отношение масс в правой части формулы (4) есть величина безразмерная. Поэтому массы т1, т2 и т можно выразить в граммах, как они даны в условии задачи. Ускорение g надо выразить в единицах СИ. После подстановки получим:
Пример 6. Маховик в виде сплошного диска радиусом R = 0,2 м и массой m = 50 кг раскручен до частоты n1 = 480 мин-1 и предоставлен сам себе. Под действием сил трения маховик остановился через t = 50 c. Найти момент М сил трения. Решение. Для решения задачи воспользуемся основным уравнением динамики вращательного движения в виде:
где Момент сил трения можно считать не изменяющимся с течением времени (Mz = const), поэтому интегрирование уравнения (1) приводит к выражению:
При вращении твердого тела относительно неподвижной оси изменение момента импульса будет равно:
где
Приравняв правые части равенств (2) и (3), получим
Момент инерции маховика в виде сплошного диска определяется по формуле: Изменение угловой скорости
Подставив в формулу (4) выражения
Проверим, дает ли расчетная формула единицу момента силы. Для этого в правую часть формулы вместо символов величин подставим их единицы:
Найденная единица (1 Н. м) является единицей момента силы. Подставим в (5) числовые значения величин и произведем вычисления, учитывая, что п1 = 480 мин -1 = 480/60 с-1 = 8 с-1:
Знак “минус” показывает, что силы трения оказывают на маховик тормозящее действие.
Пример 7. Точка совершает гармонические колебания с частотой v = 10 Гц. В момент, принятый за начальный, точка имела максимальное смещение хmax = 1 мм. Написать уравнение колебаний точки и начертить их график. Решение. Уравнение колебаний точки можно записать в виде
или
где А – амплитуда колебаний; ω – циклическая частота; t – время; j1 и j2 По определению, амплитуда колебаний А = хmax. (3) Циклическая частота ω связана с частотой ν соотношением: ω = 2πν. (4) Начальная фаза колебаний зависит от формы записи. В момент времени t = 0 формула (1) принимает вид: хmax = Аsin откуда начальная фаза
или
Изменение фазы на 2π не изменяет состояние колебательного движения, поэтому можно принять:
При использовании формулы (2) для записи уравнения колебаний получаем:
или
Аналогично находим
С учетом равенств (3) – (6) уравнения колебаний примут вид:
или
где А =1 мм = 10-3 м; ν = 10 Гц;
График соответствующего колебания приведен на рис. 3.
Пример 8. Частица массой т = 0,01 кг совершает гармонические колебания с периодом Т = 2 с. Полная энергия колеблющейся частицы Е = 0,1 мДж. Определить амплитуду А колебаний и наибольшее значение силы Fmax, действующей на частицу. Решение. Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы:
где ω = 2π/Т. Отсюда амплитуда
Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением F = -kx, где k – коэффициент квазиупругой силы; х – смещение колеблющейся точки. Максимальной сила будет при максимальном смещении хmax, равном амплитуде: Fmax = kA. (2) Коэффициент k выразим через период колебаний:
Подставив выражения k и A в формулу (2) и произведя упрощения, получим: Fmax=. Произведем вычисления:
Fmax = Пример 9. Определить число N молекул, содержащихся в объеме V = 1 мм3 воды, и массу m1 молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекул. Решение. Число N молекул, содержащихся в некоторой системе массой т, равно произведению постоянной Авогадро NА на количество вещества ν: N = νNA. Так как ν = m/M, где M – молярная масса, то N = (m/M)NA. Выразим в этой формуле массу как произведение плотности на объем V, получим: N = ρV NA/M. Произведем вычисления, учитывая, что М = 18·10-3 кг/моль (см. прил., табл. 14):
Массу т 1 одной молекулы можно найти по формуле: т 1 = М/NA. (2) Подставив в (2) значения М и NA, найдем массу молекулы воды:
Если молекулы воды плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая ячейка) V1 = d3, где d – диаметр молекулы. Отсюда
Объем V1 найдем, разделив молярный объем Vm на число молекул в моле, т.е. на NA: V1 = Vm / NA. (4) Подставим выражение (4) в (3):
где Vm = М/ ρ. Тогда
Проверим, дает ли правая часть выражения (5) единицу длины:
Произведем вычисления:
Пример 10. В баллоне объемом V = 10 л находится гелий под давлением p1 = 1 МПа и при температуре Т1 = 300 К. После того как из баллона было взято m = 10 г гелия, температура в баллоне понизилось до Т2 = 290 К. Определить давление p2 гелия, оставшегося в баллоне. Решение. Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, применив его к конечному состоянию газа: р2V = (m2/M)RT2, (1) где т 2 – масса гелия в баллоне в конечном состоянии; М – молярная масса гелия; R – молярная газовая постоянная. Из уравнения (1) выразим искомое давление: p2 = т 2RT2/(MV). (2) Массу т 2 гелия выразим через массу т 1, соответствующую начальному состоянию, и массу т гелия, взятого из баллона: т 2 = т 1- т. (3) Массу т 1 гелия найдем также из уравнения Менделеева-Клапейрона, применив его к начальному состоянию: т 1 = Мр1V/(RT1). (4) Подставив выражение массы т 1 в формулу (3), а затем выражение т 2 в формулу (2), найдем:
или
Проверим, дает ли формула (5) единицу давления. Для этого в ее правую часть вместо символов величин подставим их единицы. В правой части формулы два слагаемых. Очевидно, что первое из них дает единицу давления, так как состоит из двух множителей, первый из которых (Т2/Т1) – безразмерный, а второй – давление. Проверим второе слагаемое:
Паскаль является единицей давления. Произведем вычисления по формуле (5), учитывая, что М = 4·10-3 кг/моль (прил., табл. 14):
Пример 11. Баллон содержит m1 = 80 г кислорода и m2 = 320 г аргона. Давление смеси р = 1 МПа, температура Т = 300 К. Принимая данные газы за идеальные, определить объем V баллона. Решение. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. По уравнению Менделеева – Клапейрона парциальные давления р1 кислорода и р2 аргона выражаются формулами:
Следовательно, по закону Дальтона давление смеси газов р = р 1+ р 2, или откуда объем баллона
Произведем вычисления, учитывая, что М1 = 32·10-3 кг/моль, М2 = 40·10-3 кг/моль (прил., табл. 14):
Пример 12. Найти среднюю кинетическую энергию <εвращ> вращательного движения одной молекулы кислорода при температуре Т = 350 К, а также кинетическую энергию Ек вращательного движения всех молекул кислорода массой m = 4 г. Решение. На каждую степень свободы молекулы газа приходится одинаковая средняя энергия <ε1> = 1/2kT, где k – постоянная Больцмана; Т – термодинамическая температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная) соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода равна: <εвращ> = 2·1/2kT = kT. (1) Кинетическая энергия вращательного движения всех молекул газа: Ек = <εвращ>N. (2) Число всех молекул газа: N = NA ν, (3) где NA – постоянная Авогадро; ν – количество вещества. Если учесть, что количество вещества ν = т /М, где т – масса газа; М – молярная масса газа, то формула (3) примет вид N = NA т /М. Подставив в выражение N в формулу (2), получим Ек= NA т <εвращ> /М. (4) Произведем вычисления, учитывая, что для кислорода М=32×10-3 кг/моль (прил., табл. 14): <εвращ> = kT = 1,38·10-23·350 Дж = 4,83·10-21 Дж;
Пример 13. Вычислить удельные теплоемкости при постоянном объеме сν и при постоянном давлении ср неона и водорода, принимая эти газы за идеальные. Решение. Удельные теплоемкости идеальных газов выражаются формулами:
где i – число степеней свободы молекулы газа; М – молярная масса. Для неона (одноатомный газ) i=3 и М =20·10-3 кг/моль (прил., табл. 14). Произведем вычисления:
Для водорода (двухатомный газ) i =5 и М =2·10-3 кг/моль. Тогда
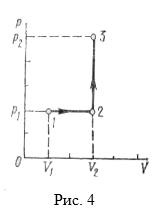
Пример 14. Кислород массой m = 2 кг занимает объем V1 = 1 м3 и находится под давлением р1 = 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V2 = 3 м3, а затем при постоянном объеме до давления р3 = 0,5 МПа. Найти изменение ∆U внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса. Решение. Изменение внутренней энергии газа
где i – число степеней свободы молекул газа (для двухатомных молекул кислорода i =5); ∆Т=Т3-Т1 разность температур газа в конечном (третьем) и начальном состояниях. Начальную и конечную температуру газа найдем из уравнения Менделеева-Клапейрона pV = (m/M)RT, откуда T = pVM/(mR). Работа расширения газа при постоянном давлении выражается формулой: А1 = m1/MR ∆ T. Работа газа, нагреваемого при постоянном объеме, равна нулю, т.е. А2 = 0. Следовательно, полная работа, совершаемая газом, А = А1+А2 = А1. Согласно первому началу термодинамики теплота Q, переданная газу, равна сумме изменения внутренней энергии ∆ U и работы А: Q = ∆ U+A. Произведем вычисления, учтя, что для кислорода М = 32·10-3 кг/моль (прил., табл. 14):
График процесса приведен на рисунке 4.
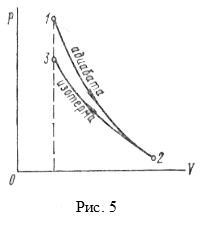
Пример 15. В цилиндре под поршнем находится водород массой m = 0,02 кг при температуре Т1 = 300 К. Водород сначала расширялся адиабатно, увеличив свой объем в п1 = 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в п2 = 5 раз. Найти температуру в конце адиабатного расширения и работу, совершенную газом при этих процессах. Изобразить процесс графически.
где γ – отношение теплоемкостей газа при постоянном давлении и постоянном объеме; n1 = V2/V1. Отсюда получаем следующее выражение для конечной температуры:
Работа А1 газа при адиабатном расширении может быть определена по формуле:
где СV – молярная теплоемкость газа при постоянном объеме. Работа А2 газа при изотермическом процессе может быть выражена в виде
где n2 = V2/V3.
Так как 50,4 = 1,91 (находится логарифмированием), то
Знак «минус» показывает, что при сжатии работа газа совершается над газом внешними силами. График процесса приведен на рисунке 5. Пример 16. Тепловая машина работает по обратимому циклу Карно. Температура теплоотдатчика Т1 = 500 К. определить термический КПД. η цикла и температуру Т2 теплоприемника тепловой машины, если за счет каждого килоджоуля теплоты, полученной от теплоотдатчика, машина совершает работу А = 350 Дж. Решение. Термический КПД тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу. Термический КПД. выражается формулой: η = А/Q1, где Q1 – теплота, полученная от теплоотдатчика; А – работа, совершенная рабочим телом тепловой машины. Зная КПД цикла, можно по формуле η = (Т1-Т2)/Т1 определить температуру охладителя Т2: Т2 = Т1(1- η). Произведем вычисления: η = 350/1000 = 0,35; Т2 = 500(1-0,35) К = 325 К.
II. Основы электродинамики
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 379; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.111 (0.013 с.) |

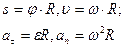
 ,
,
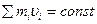

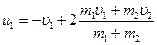 ;
;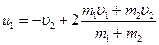 ; неупругого
; неупругого 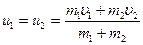 ;
;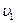 и
и 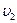 -скорости частиц до столкновения
-скорости частиц до столкновения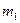 и
и 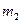 -массы частиц
-массы частиц
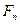 -сила нормального давления
-сила нормального давления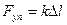 ,
, -деформация
-деформация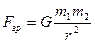 ,
,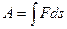
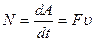
 ;
;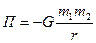 ;
;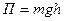 ,
,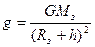 ,
, -масса Земли;
-масса Земли; -радиус Земли;
-радиус Земли;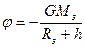

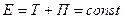
 ,
, ;
;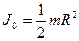 ;
;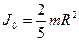 ;
;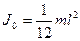 .
.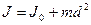 ,
, -момент инерции относительно
-момент инерции относительно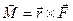 ,
,


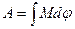
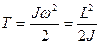
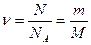 ,
, -постоянная Авогадро;
-постоянная Авогадро;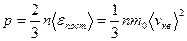 ,
,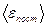 -средняя кинетическая энергия
-средняя кинетическая энергия -масса молекулы;
-масса молекулы;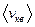 -средняя квадратичная скорость.
-средняя квадратичная скорость.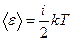 ,
,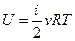 .
.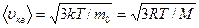 ;
; .
. .
.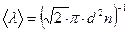 ,
,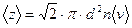 .
. ,
,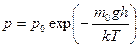
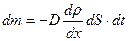 ,
, -плотность;
-плотность;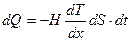 ,
,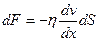 ,
,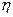 - динамическая вязкость.
- динамическая вязкость.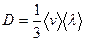 ,
, ,
,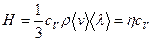 ,
,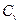 -удельная изохорная теплоемкость.
-удельная изохорная теплоемкость.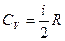 ;
;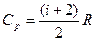
 ;
;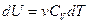 ;
;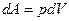 .
.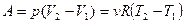 ;
;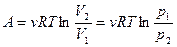 ;
;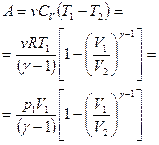
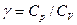
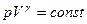 ;
;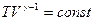 ;
;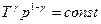 .
. ,
, и
и  - количество теплоты, переданное
- количество теплоты, переданное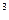 . Найти координату х, скорость υ и ускорение а точки в момент времени t = 2 с.
. Найти координату х, скорость υ и ускорение а точки в момент времени t = 2 с.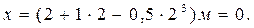
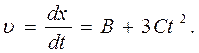

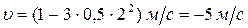 ;
;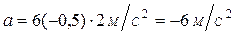
 , где A = 10 рад, B = 20 рад/с, C = -2 рад/c2.Найти полное ускорение точки, находящейся на расстоянии r = 0,1 м от оси вращения для момента времени
, где A = 10 рад, B = 20 рад/с, C = -2 рад/c2.Найти полное ускорение точки, находящейся на расстоянии r = 0,1 м от оси вращения для момента времени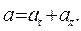
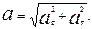 (1)
(1) Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами:
Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами:
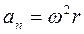 , (2)
, (2)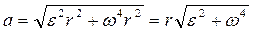 (2)
(2)

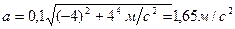 .
. системы в начальном состоянии (в данном случае перед выстрелом) равна полной энергии
системы в начальном состоянии (в данном случае перед выстрелом) равна полной энергии 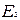 в конечном состоянии (когда пуля поднялась на высоту h), т.е.
в конечном состоянии (когда пуля поднялась на высоту h), т.е. .
. а в конечном состоянии – потенциальной энергии пули на высоте h, т.е.
а в конечном состоянии – потенциальной энергии пули на высоте h, т.е. . (2)
. (2)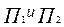 в формулу (2), найдем
в формулу (2), найдем 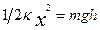 , откуда
, откуда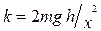 . (3)
. (3)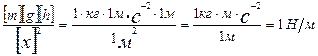 .
. .
.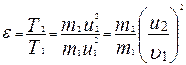 , (1)
, (1)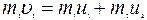 ; (2)
; (2)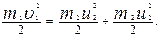 (3)
(3)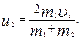
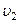 и т 1, получим:
и т 1, получим: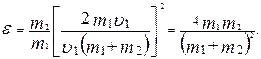
 предоставить самим себе? Трением и массой нити пренебречь.
предоставить самим себе? Трением и массой нити пренебречь. т1g - Т1 = т1а
т1g - Т1 = т1а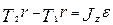 (3)
(3) - момент инерции блока (сплошного диска) относительно оси Z.
- момент инерции блока (сплошного диска) относительно оси Z. ,
, 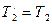 . Воспользовавшись этим, подставим в уравнение (3) вместо
. Воспользовавшись этим, подставим в уравнение (3) вместо  и
и  выражения
выражения  и
и  , получив их предварительно из уравнений (1) и (2):
, получив их предварительно из уравнений (1) и (2): .
.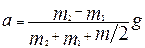 . (4)
. (4)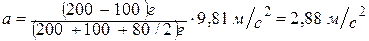 .
. , (1)
, (1) - изменение момента импульса маховика, вращающегося относительно оси Z, совпадающей с геометрической осью маховика, за интервал времени dt; Mz - момент внешних сил (в данном случае момент сил трения), действующих на маховик относительно той же оси.
- изменение момента импульса маховика, вращающегося относительно оси Z, совпадающей с геометрической осью маховика, за интервал времени dt; Mz - момент внешних сил (в данном случае момент сил трения), действующих на маховик относительно той же оси.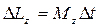 . (2)
. (2)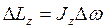 , (3)
, (3)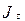 - момент инерции маховика относительно оси Z;
- момент инерции маховика относительно оси Z;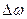 - изменение угловой скорости маховика.
- изменение угловой скорости маховика.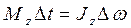 , откуда
, откуда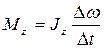 . (4)
. (4)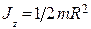 .
. выразим через конечную п2 и начальную п1 частоты вращения, пользуясь соотношением
выразим через конечную п2 и начальную п1 частоты вращения, пользуясь соотношением 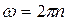 :
: .
.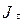 и
и 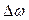 , получим:
, получим: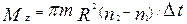 . (5)
. (5) .
.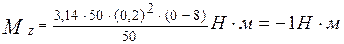 .
.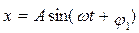 (1)
(1)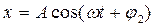 , (2)
, (2) - начальные фазы, соответствующие формы записи (1) или (2).
- начальные фазы, соответствующие формы записи (1) или (2).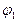 ,
,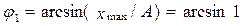
 (k = 0, 1, 2,…).
(k = 0, 1, 2,…).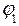 = π/2. (5)
= π/2. (5)
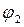 =2πk (k = 0, 1, 2, 3,…).
=2πk (k = 0, 1, 2, 3,…).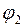 =0. (6)
=0. (6)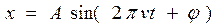 ,
, ,
,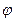 = π/2.
= π/2.
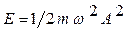 ,
, . (1)
. (1) . (3)
. (3)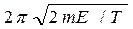
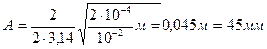 ;
; .
.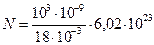 молекул = 3,34·1019 молекул.
молекул = 3,34·1019 молекул.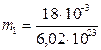 кг = 2,99·10-26 кг.
кг = 2,99·10-26 кг.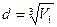 . (3)
. (3)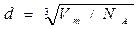 ,
, . (5)
. (5)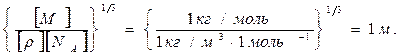
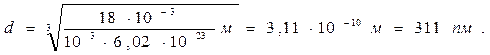
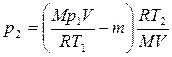
 . (5)
. (5)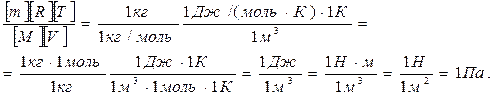
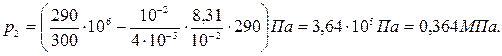
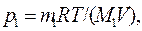


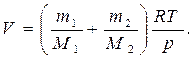
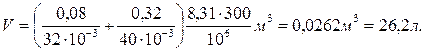
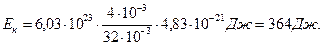
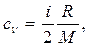 (1)
(1)  (2)
(2)
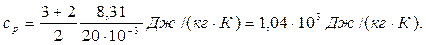
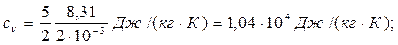

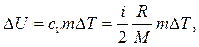 (1)
(1)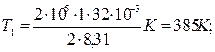
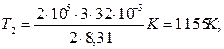

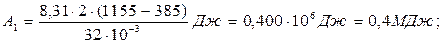

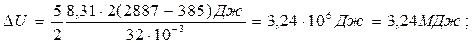

 Решение. Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением:
Решение. Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением: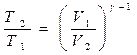 или
или  ,
,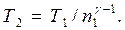
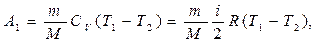
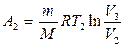 или
или 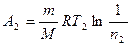 ,
, Произведем вычисления, учитывая, что для водорода как двухатомного газа γ = 1,4, i = 5 и М = 2·10-3 кг/моль:
Произведем вычисления, учитывая, что для водорода как двухатомного газа γ = 1,4, i = 5 и М = 2·10-3 кг/моль: