
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волновое число, фазовая скорость волны. Уравнение сферической волны. Волновое уравнение.Содержание книги
Поиск на нашем сайте
Равнение бегущей волны, фазовая скорость и волновое уравнение Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова (по имени русского ученого Н. А. Умова (1846—1915), решившего задачу о распространении энергии в среде). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. Для вывода уравнения бегущей волны — зависимости смещения колеблющейся частицы от координат и времени — рассмотрим плоскую волну,предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распространения волны (рис. 220). В данном случае волновые поверхности перпендикулярны оси х, а так как все точки волновой поверхности колеблются одинаково, то смещение x будет зависеть только от x и t, т. е. x = x (x, t). На рис. 220 рассмотрим некоторую частицу В среды, находящуюся от источника колебаний О на расстоянии х. Если колебания точек, лежащих в плоскости х= 0,описываются функцией x (0, t) = A cos wt, то частица В среды колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на t, так как для прохождения волной расстояния х требуется время t = x / v, где v — скорость распространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид
откуда следует, что x (х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то
В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид
где А = const — амплитуда волны, w — циклическая частота, j 0 — начальная фаза волны, определяемая в общем случае выбором начал отсчета х и t, [ w (t—x/v)+ j 0] — фаза плоской волны. Для характеристики волн используется волновое число
Учитывая (154.3), уравнению (154.2) можно придать вид
Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (154.4) только знаком члена kx. Основываясь на формуле Эйлера (140.7), уравнение плоской волны можно записать в виде
где физический смысл имеет лишь действительная часть. Предположим, что при волновом процессе фаза постоянна, т. е.
Продифференцировав выражение (154.5) и сократив на w, получим
Следовательно, скорость v распространения волны в уравнении (154.6) есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью. Повторяя ход рассуждений для плоской волны, можно доказать, что уравнение сферической волны — волны, волновые поверхности которой имеют вид концентрических сфер, записывается как
где r — расстояние от центра волны до рассматриваемой точки среды. В случае сферической волны даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону 1/ r. Уравнение (154.7) справедливо лишь для r, значительно превышающих размеры источника (тогда источник колебаний можно считать точечным). Из выражения (154.3) вытекает, что фазовая скорость
Если фазовая скорость воли в среде зависит от их частоты, то это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой. Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных
или
где v — фазовая скорость,
Образование стоячих волн, уравнение стоячей волны. Если в среде распространяется несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Волны накладываются друг на друга, не возмущая (не искажая друг друга). Это и есть принцип суперпозиции волн. Если две волны, приходящие в какую-либо точку пространства, обладают постоянной разностью фаз, такие волны называются когерентными. При сложении когерентных волн возникает явление интерференции. Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении от преград. Напишем уравнения двух плоских волн, распространяющихся в противоположных направлениях (начальная фаза
Сложим уравнения и преобразуем по формуле суммы косинусов (5.4.3):
Т.к.
Учитывая, что
В выражении для фазы не входит координата, поэтому можно записать:
где суммарная амплитуда В точках, где координаты удовлетворяют условию
В точках, координаты которых удовлетворяют условию
Точки среды, находящиеся в узлах, колебаний не совершают. Образование стоячих волн наблюдают при интерференции бегущей и отраженных волн. На границе, где происходит отражение волны, получается пучность, если среда, от которой происходит отражение, менее плотная (рис. 5.5, а), и узел – если более плотная (рис. 5.5, б). Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.170.80 (0.005 с.) |

 (154.1)
(154.1)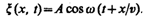
 (154.2)
(154.2) (154.3)
(154.3) (154.4)
(154.4)
 (154.5)
(154.5) откуда
откуда (154.6)
(154.6) (154.7)
(154.7)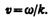 (154.8)
(154.8)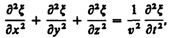
 (154.9)
(154.9) — оператор Лапласа. Решением уравнения (154.9) является уравнение любой волны. Соответствующей подстановкой можно убедиться, что уравнению (154.9) удовлетворяют, в частности, плоская волна (см. (154.2)) и сферическая волна (см. (154.7)). Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид
— оператор Лапласа. Решением уравнения (154.9) является уравнение любой волны. Соответствующей подстановкой можно убедиться, что уравнению (154.9) удовлетворяют, в частности, плоская волна (см. (154.2)) и сферическая волна (см. (154.7)). Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид (154.10)
(154.10) ):
): .
.
 .
. , то можно записать:
, то можно записать: .
. , получим уравнение стоячей волны:
, получим уравнение стоячей волны: .
.
 ,
,
 .
.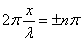 (n = 1, 2, 3, …),
(n = 1, 2, 3, …), 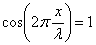 , суммарная амплитуда равна максимальному значению:
, суммарная амплитуда равна максимальному значению:  , – это пучности стоячей волны. Координаты пучностей:
, – это пучности стоячей волны. Координаты пучностей: .
.

 (n = 0, 1, 2,…),
(n = 0, 1, 2,…),  и суммарная амплитуда колебаний равна нулю
и суммарная амплитуда колебаний равна нулю 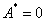 , – это узлы стоячей волны. Координаты узлов:
, – это узлы стоячей волны. Координаты узлов: .
.



