
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод дифференциальных уравнений колебаний для физического и математического маятников, частоты и периоды собственных колебаний маятников. Математический маятник.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гармонические колебания. Основные характеристики гармонических колебаний: амплитуда, частота, фаза, период колебаний. Дифференциальное уравнение гармонических колебаний. Представление гармонического колебания с помощью векторной диаграммы.
Сила трения для малых скоростей движения. Вывод дифференциального уравнения для колебаний груза на пружине с учетом силы трения. Зависимость смещения груза из положения равновесия от времени. Частота, период и амплитуда затухающих колебаний. Вынужденные колебания. Все реальные колебания являются затухающими. Чтобы реальные колебания происходили достаточно долго нужно периодически пополнять энергию колебательной системы, действуя на нее внешней периодически изменяющейся силой Рассмотрим явление колебаний, если внешняя (вынуждающая) сила изменяется в зависимости от времени по гармоническому закону. При этом в системах возникнут колебания, характер которых в той или иной мере повторит характер вынуждающей силы. Такие колебания называются вынужденными. Вынуждающая сила гармонического вида. Вывод дифференциального уравнения вынужденных колебаний для груза на пружине и колебательного контура. Амплитуда установившихся вынужденных колебаний. Амплитудные резонансные кривые для различных значений коэффициента затухания. Резонанс. Фронт волны. Длина волны. На рис. 1 и 2 показаны колебания частиц, положения равновесия которых лежат на оси х. В действительности колеблются не только частицы, расположенные вдоль оси х, а совокупность частиц, заключенных в некотором объеме. Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые части пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом). Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт каждый момент времени только один. Волновые поверхности остаются неподвижными. Волновой фронт все время перемещается. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, в сферической волне — множество концентрических сфер. Рассмотрим случай, когда плоская волна распространяется вдоль оси х. Тогда все точки среды, положения равновесия которых имеют одинаковую координату х (но различные значения координат y и z), колеблются в одинаковой фазе.
Рисунок 4 На рис. 3 изображена кривая, которая дает смещение Расстояние где v – скорость волны, Т – период колебаний. Длину волны можно определить также как расстояние между ближайшими точками среды, колеблющимися с разностью фаз, равной 2П. Заменив в соотношении (1.1) Т через 1/
Рассмотрев кратко основные понятия, связанные с волной, перейдем к описательной стороне, т.е. волновому уравнению.
Глава II. Волновое уравнение. Математические сведения. Этот параграф является математическим введением к тому динамическому рассмотрению волн, которое будет дано в $2. Рассмотрим произвольную функцию f(at-bx) (2.3) от аргумента аt—bх. Продифференцируем ее дважды по t: Здесь штрих означает дифференцирование по аргументу at—bx. Продифференцируем теперь нашу функцию дважды по х: Сравнивая (2.4) и (2.5), мы убеждаемся, что функция (2.3) удовлетворяет уравнению где u=a/b. Легко видеть, что этому же уравнению удовлетворяет произвольная функция f(at+bx) (2.7) (2.7) аргумента at+bx, а также сумма функций вида (2.3) и (2.7). Функции (2.3) и (2.7) изображают при положительных a, b плоские волны, распространяющиеся, не деформируясь, со скоростью и в сторону соответственно возрастающих или убывающих значений х **). Уравнение (2.6)—дифференциальное уравнение в частных производных, играющее в физике очень важную роль. Оно называется волновым уравнением. В математических курсах доказывается, что оно не имеет решений, отличных от тех, которые могут быть представлены функциями вида (2.3) и (2.7) или суперпозицией таких функций, например, f1(at - bх) + f2(at+bx). Всякий раз, когда из физических соображений можно установить, что та или иная физическая величина s удовлетворяет уравнению вида мы сможем на основании сообщенных здесь математических сведений заключить, что процесс изменений этой величины носит характер плоской, волны, распространяющейся в ту или другую сторону со скоростью и, или суперпозиции таких волн. Вид функций f1, f2 определяется характером движения источника волн, а также явлениями, происходящими на границе среды. Пусть источником волн является плоскость х =0, причем на этой плоскости величина S колеблется но закону s =Acoswt. В этом случае от плоскости х= 0 распространяются вправо и влево волны s= Acos(wt Из линейности волнового уравнения следует, что если ему удовлетворяют функции s1, s2,s3,... в отдельности, то ему удовлетворяет также функция S == S1 + S2 + S3 +... (принцип, суперпозиции). Рассмотрим несколько примеров. а) Волновому уравнению удовлетворяют синусоидальные бегущие волны s1 = Aсоs(wt — kx ), s2= Acos(wt+kx). На основании принципа суперпозиции волновому уравнению удовлетворяет стоячая волна s=2Acoskx coswt являющаяся суперпозицией только что рассмотренных синусоидальных бегущих волн. б) Волновому уравнению на основании принципа суперпозиции удовлетворяет всякая функция вида S= Это—функция вида f(at—bx); она изображает несинусоидальную волну, распространяющуюся без деформации в сторону возрастающих х.
Упругие волны в стержне. Волновое уравнение. В предыдущем параграфе мы рассмотрели математическую сторону волнового уравнения. В этом же параграфе я хотел бы на конкретном примере рассмотреть как работает тот математический аппарат.
Рисунок 4 Применим второй закон Ньютона и закон сложения сил к движению куска стержня, заключенного между двумя плоскостями x и х+ слева стоит произведение массы куска на ускорение д2 Разделим уравнение на S0 Перейдя к пределу при справедливое в каждой точке стержня. Оно указывает, что ускорение данной точки пропорционально частной производной напряжения по ж в этой точке.
Подставляя в (2.8) соотношение (2.7), получим:
Вспомнив теперь формулу, содержащую определение деформации, и подставив ее в (2.9), получаем: Образование стоячих волн, уравнение стоячей волны. Если в среде распространяется несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Волны накладываются друг на друга, не возмущая (не искажая друг друга). Это и есть принцип суперпозиции волн. Если две волны, приходящие в какую-либо точку пространства, обладают постоянной разностью фаз, такие волны называются когерентными. При сложении когерентных волн возникает явление интерференции. Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении от преград. Напишем уравнения двух плоских волн, распространяющихся в противоположных направлениях (начальная фаза
Сложим уравнения и преобразуем по формуле суммы косинусов (5.4.3):
Т.к.
Учитывая, что
В выражении для фазы не входит координата, поэтому можно записать:
где суммарная амплитуда В точках, где координаты удовлетворяют условию
В точках, координаты которых удовлетворяют условию
Точки среды, находящиеся в узлах, колебаний не совершают. Образование стоячих волн наблюдают при интерференции бегущей и отраженных волн. На границе, где происходит отражение волны, получается пучность, если среда, от которой происходит отражение, менее плотная (рис. 5.5, а), и узел – если более плотная (рис. 5.5, б). Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. Согласно молекулярной теории света, под действием электромагнитного поля световой волны в молекулах среды происходит смещение связующих пар внешних (оптических) электронов в сторону более электроотрицательного атома. Это смещение приводит к несовпадению центров положительных и отрицательных зарядов, т.е. молекулы поляризуются и приобретают характер диполей. Диполи совершают вынужденные колебания с частотой, равной частоте падающей световой волны. Кроме того, данные диполи являются источниками вторичных сферических волн. Если среда однородна и изотропна (свойства среды одинаковы во всех направлениях) и падающая световая волна плоская, то из-за интерференции ее со всеми вторичными волнами, излучаемыми диполями среды, получается плоская результирующая волна, которая распространяется в соответствии с законами преломления и отражения света. Так как распространение света в преломляющей среде связано с поляризуемостью ее молекул, то различные соединения, среды и вещества имеют разную преломляющую способность. Основные законы оптики, полное отражение Еще до установления природы света были известны следующие основные законы оптики: закон прямолинейного распространения света в оптически однородной среде; закон независимости световых пучков (справедлив только в линейной оптике); закон отражения света; закон преломления света. Закон прямолинейного распространения света: свет в оптически однородной среде распространяется прямолинейно. Доказательством этого закона является наличие тени с резкими границами от непрозрачных предметов при освещении их точечными источниками света (источники, размеры которых значительно меньше освещаемого предмета и расстояния до него). Тщательные эксперименты показали, однако, что этот закон нарушается, если свет проходит сквозь очень малые отверстия, причем отклонение от прямолинейности распространения тем больше, чем меньше отверстия. Закон независимости световых пучков: эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены. Разбивая световой поток на отдельные световые пучки (например, с помощью диафрагм), можно показать, что действие выделенных световых пучков независимо. Если свет падает на границу раздела двух сред (двух прозрачных веществ), то падающий луч I (рис. 229) разделяется на два — отраженный II и преломленный III, направления которых задаются законами отражения и преломления. Закон отражения: отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения; угол i '1 отражения равен углу i 1 падения:
Закон преломления: луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред:
где n 21 — относительный показатель преломления второй среды относительно первой. Индексы в обозначениях углов i 1, i '1, i 2 указывают, в какой среде (первой или второй) идет луч. Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления:
Абсолютным показателем преломления среды называется величина n, равная отношению скорости c электромагнитных волн в вакууме к их фазовой скорости v в среде:
Сравнение с формулой (162.3) дает, что
Из симметрии выражения (165.4) вытекает обратимость световых лучей. Если обратить луч III (рис.229), заставив его падать на границу раздела под углом i 2, то преломленный луч в первой среде будет распространяться под углом i 1, т. е. пойдет в обратном направлении вдоль луча I. Если свет распространяется из среды с большим показателем преломления n 1 (оптически более плотной) в среду с меньшим показателем преломления n 2(оптически менее плотную) (n 1> n 2), например из стекла в воду, то, согласно (165.4),
Отсюда следует, что преломленный луч удаляется от нормали и угол преломления i 2 больше,чем угол падения i 1 (рис. 230, а).С увеличением угла падения увеличивается угол преломления (рис. 230, б, в) до тех пор, пока при некотором угле падения (i 1= i пр) угол преломления не окажется равным p /2. Угол i пр называется предельным углом. При углах падения i 1> i пр весь падающий свет полностью отражается (рис. 230, г). По мере приближения угла падения к предельному интенсивность преломленного луча уменьшается, а отраженного — растет (рис. 230, а—в). Если i 1= i пр, то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего (рис. 230, г). Таким образом, при углах падения в пределах от i пр до p /2 луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы. Это явление называется полным отражением.
Предельный угол i пр определим из формулы (165.4) при подстановке в нее i 2= p /2. Тогда
Уравнение (165.5) удовлетворяет значениям угла i пр при n 2£ n 1. Следовательно, явление полного отражения имеет место только при падении света из среды оптически более плотной в среду оптически менее плотную. Явление полного отражения используется в призмах полного отражения Показатель преломления стекла равен n» 1,5, поэтому предельный угол для границы стекло — воздух равен i пр=arcsin(1/1,5)=42°. Поэтому при падении света на границу стекло — воздух при i > 42° всегда будет иметь место полное отражение. На рис. 231, а—в показаны призмы полного отражения, позволяющие: а) повернуть луч на 90°; б) повернуть изображение; в) обернуть лучи. Такие призмы применяются в оптических приборах (например, в биноклях, перископах), а также в рефрактометрах, позволяющих определять показатели преломления тел (по закону преломления, измеряя i пр, находим относительный показатель преломления двух сред, а также абсолютный показатель преломления одной из сред, если показатель преломления другой среды известен).
Явление полного отражения используется также в световодах (светопроводах), представляющих собой тонкие, произвольным образом изогнутые нити (волокна) из оптически прозрачного материала. В волоконных деталях применяют стеклянное волокно, световедущая жила (сердцевина) которого окружается стеклом — оболочкой из другого стекла с меньшим показателем преломления. Свет, падающий на торец световода под углами, большими предельного, претерпевает на поверхности раздела сердцевины и оболочки полное отражение н распространяется только по световедущей жиле. Таким образом, с помощью световодов можно как угодно искривлять путь светового пучка. Диаметр световедущих жил лежит в пределах от нескольких микрометров до нескольких миллиметров. Для передачи изображений, как правило, применяются многожильные световоды. Вопросы передачи световых волн и изображений изучаются в специальном разделе оптики — волоконной оптике, возникшей в 50-е годы XX столетия. Световоды используются в электронно-лучевых трубках, в электронно-счетных машинах, для кодирования информации, в медицине (например, диагностика желудка), для целей интегральной оптики и т. д.
15. Тонкие линзы. Формула линзы (без вывода). Построение изображений в тонкой линзе.
Раздел оптики, в котором законы распространения света рассматриваются на основе представления о световых лучах, называется геометрической оптикой. Под световыми лучами понимают нормальные к волновым поверхностям линии, вдоль которых распространяется поток световой энергии. Геометрическая оптика, оставаясь приближенным методом построения изображений в оптических системах, позволяет разобрать основные явления, связанные с прохождением через них света, и является поэтому основой теории оптических приборов. Линзы представляют собой прозрачные тела, ограниченные двумя поверхностями (одна из них обычно сферическая, иногда цилиндрическая, а вторая — сферическая или плоская), преломляющими световые лучи, способные формировать оптические изображения предметов. Материалом для линз служат стекло, кварц, кристаллы, пластмассы и т. п. По внешней форме (рис. 232) линзы делятся на: 1) двояковыпуклые; 2) плосковыпуклые; 3) двояковогнутые; 4) плосковогнутые; 5) выпукло-вогнутые; 6) вогнуто-выпуклые. По оптическим свойствам линзы делятся на собирающие и рассеивающие. Линза называется тонкой, если ее толщина (расстояние между ограничивающими поверхностями) значительно меньше по сравнению с радиусами поверхностей, ограничивающих линзу. Прямая, проходящая через центры кривизны поверхностей линзы, называется главной оптической осью. Для всякой линзы существует точка, называемая оптическим центром линзы, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь. Оптический центр О линзы для простоты будем считать совпадающим с геометрическим центром средней части линзы (это справедливо только для двояковыпуклой и двояковогнутой линз с одинаковыми радиусами кривизны обеих поверхностей; для плосковыпуклых и плосковогнутых линз оптический центр О лежит на пересечении главной оптической оси со сферической поверхностью). Для вывода формулы тонкой линзы — соотношения, связывающего радиусы кривизны изображения, — воспользуемся принципом Ферма*, или принципом наименьшего времени: действительный путь распространения света (траектория светового луча) есть путь, для прохождения которого свету требуется минимальное время по сравнению с любым другим мыслимым путем между теми же точками. Рассмотрим два световых луча (рис. 233) — луч, соединяющий точки А и В (луч ЛОВ), и луч, проходящий через край линзы (луч АСВ), — воспользовавшись условием равенства времени прохождения света вдоль АО В и АСВ. Время прохождения света вдоль АОВ
где солютные показатели преломления линзы и окружающей среды). Время прохождения света вдоль АСВ равно
Рассмотрим параксиальные (приосевые) луча, т. с. лучи, образующие с оптической осью малые углы. Только при использовании параксиальных лучей получается стигматическое изображение, т. е. все лучи параксиального пучка, исходящего из точки А, пересекают оптическую ось в одной и той же точке В. Тогда
Аналогично,
Подставив найденные выражения в (166.1), получим
Для тонкой линзы
Выражение (166.3) представляет собой формулу тонкой линзы. Радиус кривизны выпуклой поверхности линзы считается положительным, вогнутой — отрицательным. Если
Соответствующее этому случаю расстояние Ь = OF=f называется фокусным расстоянием линзы, определяемым по формуле
Оно зависит от относительного показателя преломления и радиусов кривизны. Если выходят из линзы параллельным пучком (рис. 234, б), то a=OF=f. Таким образом, фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны. Точки F, лежащие по обестороны линзы на расстоянии, равном фокусному, называются фокусами линзы. Фокус — это точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси. Величина
называется оптической силой линзы. Ее единица — диоптрия (дптр). Диоптрия — оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр= 1/м. Линзы с положительной оптической силой являются собирающими, с отрицательной — рассеивающими. Плоскости, проходящие через фокусы линзы перпендикулярно ее главной оптической оси, называются фокальными плоскостями. В отличие от собирающей рассеивающая линза имеет мнимые фокусы. В мнимом фокусе сходятся (после преломления) воображаемые продолжения лучей, падающих на рассеивающую линзу параллельно главной оптической оси (рис. 235).
|

 (1) где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А. Определенные состояния системы, которая совершает гармонические колебания, повторяются через промежуток времени Т, имеющий название период колебания, за который фаза колебания получает приращение (изменение) 2π, т. е.
(1) где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А. Определенные состояния системы, которая совершает гармонические колебания, повторяются через промежуток времени Т, имеющий название период колебания, за который фаза колебания получает приращение (изменение) 2π, т. е.  откуда
откуда  (2) Величина, обратная периоду колебаний,
(2) Величина, обратная периоду колебаний,  (3) т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем
(3) т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем  Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса. Найдем первую и вторую производные по времени от величины s, совершающей гармонические колебания:
Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса. Найдем первую и вторую производные по времени от величины s, совершающей гармонические колебания:  (4)
(4)  (5) т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин в формулах (4) и (5) соответственно равны Аω0 и Аω02. Фаза величины в формуле (4) отличается от фазы величины в формуле (1) на π/2, а фаза величины в выражении (5) отличается от фазы величины (1) на π. Значит, в моменты времени, когда s=0, ds/dt имеет наибольшие значения; когда же s становится равным максимальному отрицательному значению, то d2s/dt2 равен наибольшему положительному значению (рис. 1).
(5) т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин в формулах (4) и (5) соответственно равны Аω0 и Аω02. Фаза величины в формуле (4) отличается от фазы величины в формуле (1) на π/2, а фаза величины в выражении (5) отличается от фазы величины (1) на π. Значит, в моменты времени, когда s=0, ds/dt имеет наибольшие значения; когда же s становится равным максимальному отрицательному значению, то d2s/dt2 равен наибольшему положительному значению (рис. 1).
 Рис.1
Из выражения (5) непосредственно вытекает дифференциальное уравнение гармонических колебаний
Рис.1
Из выражения (5) непосредственно вытекает дифференциальное уравнение гармонических колебаний  (6) (где s = A cos(ω0t+φ)). Решением данного дифференциального уравнения является выражение (1). Гармонические колебания графически изображаются методом вращающегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки О, которая выбрана на оси х, под углом φ, который равен начальной фазе колебания, откладывается вектор А, у которого модуль равен амплитуде А рассматриваемого колебания (рис. 2). Если данный вектор привести во вращение с угловой скоростью ω0, которая равна циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения от –А до +А, а колеблющаяся величина будет изменяться со временем по закону s = Acos(ω0t+φ). Значит, гармоническое колебание можно представить как проекцию на некоторую выбранную произвольным образом ось вектора амплитуды А, который отложен из произвольной точки оси под углом φ, равным начальной фазе, и вращающегося с угловой скоростью ω0 вокруг этой точки.
(6) (где s = A cos(ω0t+φ)). Решением данного дифференциального уравнения является выражение (1). Гармонические колебания графически изображаются методом вращающегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки О, которая выбрана на оси х, под углом φ, который равен начальной фазе колебания, откладывается вектор А, у которого модуль равен амплитуде А рассматриваемого колебания (рис. 2). Если данный вектор привести во вращение с угловой скоростью ω0, которая равна циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения от –А до +А, а колеблющаяся величина будет изменяться со временем по закону s = Acos(ω0t+φ). Значит, гармоническое колебание можно представить как проекцию на некоторую выбранную произвольным образом ось вектора амплитуды А, который отложен из произвольной точки оси под углом φ, равным начальной фазе, и вращающегося с угловой скоростью ω0 вокруг этой точки.
 Рис.2
В физике часто используется другой метод, отличающийся от метода вращающегося вектора амплитуды лишь по форме. В данном методе колеблющуюся величину представляют комплексным числом. Используя формулу Эйлера, для комплексных чисел
Рис.2
В физике часто используется другой метод, отличающийся от метода вращающегося вектора амплитуды лишь по форме. В данном методе колеблющуюся величину представляют комплексным числом. Используя формулу Эйлера, для комплексных чисел  (7) где
(7) где 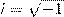 - мнимая единица. Значит уравнение гармонического колебания (1) можно представить в комплексной форме:
- мнимая единица. Значит уравнение гармонического колебания (1) можно представить в комплексной форме:  (8) Вещественная часть формулы (8)
(8) Вещественная часть формулы (8)  есть гармоническое колебание. Обозначение Re вещественной части условимся опускать и (8) записывать в форме
есть гармоническое колебание. Обозначение Re вещественной части условимся опускать и (8) записывать в форме  В теории колебаний уславливаются, что колеблющаяся величина s равна вещественной части комплексного выражения, стоящего в этом равенстве справа.
В теории колебаний уславливаются, что колеблющаяся величина s равна вещественной части комплексного выражения, стоящего в этом равенстве справа.

 из положения равновесия точек с различными x в некоторый момент времени. Не следует воспринимать этот рисунок как зримое изображение волны. На рисунке показан график функции
из положения равновесия точек с различными x в некоторый момент времени. Не следует воспринимать этот рисунок как зримое изображение волны. На рисунке показан график функции  , на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. Очевидно, что
, на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. Очевидно, что (
(  (2.4)
(2.4) (2.5)
(2.5) (2.6)
(2.6) (2.6а)
(2.6а) kx), k =
kx), k =  .
.
 в) Пусть волны S1, S2, имеющие вид коротких импульсов, распространяются навстречу одна другой. В некоторый момент моментальный снимок суперпозиции S1 + S2 этих волн имеет вид, показанный на рис. 4,а. Через некоторое время моментальный снимок волны будет иметь вид, показанный на рис. 4, б, – волны пройдут «одна сквозь другую» и притом каждая так, как будто другой не существует.
в) Пусть волны S1, S2, имеющие вид коротких импульсов, распространяются навстречу одна другой. В некоторый момент моментальный снимок суперпозиции S1 + S2 этих волн имеет вид, показанный на рис. 4,а. Через некоторое время моментальный снимок волны будет иметь вид, показанный на рис. 4, б, – волны пройдут «одна сквозь другую» и притом каждая так, как будто другой не существует.
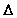 х. Масса этого куска равна р0S0
х. Масса этого куска равна р0S0 
 :
: (2.7)
(2.7) , получим уравнение
, получим уравнение (2.8)
(2.8)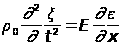 (2.9)
(2.9)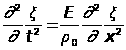
 ):
): .
.
 .
. , то можно записать:
, то можно записать: .
. , получим уравнение стоячей волны:
, получим уравнение стоячей волны: .
.
 ,
,
 .
.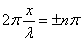 (n = 1, 2, 3, …),
(n = 1, 2, 3, …), 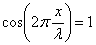 , суммарная амплитуда равна максимальному значению:
, суммарная амплитуда равна максимальному значению:  , – это пучности стоячей волны. Координаты пучностей:
, – это пучности стоячей волны. Координаты пучностей: .
.

 (n = 0, 1, 2,…),
(n = 0, 1, 2,…),  и суммарная амплитуда колебаний равна нулю
и суммарная амплитуда колебаний равна нулю 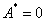 , – это узлы стоячей волны. Координаты узлов:
, – это узлы стоячей волны. Координаты узлов: .
.

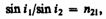 (165.1)
(165.1) (165.2)
(165.2) (165.3)
(165.3) , где e и m — соответственно электрическая и магнитная проницаемости среды. Учитывая (165.2), закон преломления (165.1) можно записать в виде
, где e и m — соответственно электрическая и магнитная проницаемости среды. Учитывая (165.2), закон преломления (165.1) можно записать в виде (165.4)
(165.4)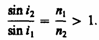

 (165.5)
(165.5)
 Тонкие линзы. Изображение предметов с помощью линз
Тонкие линзы. Изображение предметов с помощью линз поверхностей линзы с расстояниями а и b от линзы до предмета и его
поверхностей линзы с расстояниями а и b от линзы до предмета и его
 *П. Ферма (1601—1665) — французский математик и физик.
*П. Ферма (1601—1665) — французский математик и физик.
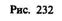


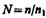 — относительный показатель преломления (n и
— относительный показатель преломления (n и  — соответственно аб-
— соответственно аб-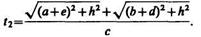
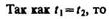


 и
и
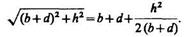


 поэтому (166.2) можно представить в виде
поэтому (166.2) можно представить в виде





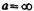 , т. е. лучи падают на линзу параллельным пучком (рис. 234, а), то
, т. е. лучи падают на линзу параллельным пучком (рис. 234, а), то

 , т. е. изображение находится в бесконечности и, следовательно, лучи
, т. е. изображение находится в бесконечности и, следовательно, лучи







