
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условие максимума и минимума интерференцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть разделение на две когерентные волны происходит в точке О (рис. 8.1).
Рис. 8.1 До точки Р первая волна проходит в среде с показателем
где
Учитывая, что
где Если разность хода равна целому числу длин волн в вакууме
то Если оптическая разность хода
то
где (φ2–φ1) – разность фаз накладывающихся колебаний. Интенсивность волны пропорциональна квадрату амплитуды колебаний, значит, для интенсивности можно записать соотношение
Из формул (4.54) и (4.55) следует, что разность фаз колебаний, обусловленных наложением в точке двух волн,
где х 1 и х 2 – расстояния, проходимые волнами от источников до точек наложения. Величина Δх = х 2 – х 1называется разностью хода волн, именно она определяет результат интерференции в каждой точке. В местах, где φ2–φ1 близко к четному числу, умноженному на π, наблюдаются максимумы интенсивности волны. Там же, где φ2–φ1 близко к нечетному числу π, наблюдаются минимумы интенсивности.
Частным случаем интерференции волн являются стоячие волны. Они образуются в результате наложения двух бегущих синусоидальных волн, которые распространяются навстречу друг другу и имеют одинаковые частоты, амплитуды и направления колебаний. Обычно это происходит при отражении бегущей волны от препятствия. Рассмотрим простейший случай, когда прямая и обратная волны распространяются вдоль оси х и описываются формулами:
В каждой точке оси происходит сложение этих колебаний. Используем тригонометрическую формулу суммы двух косинусов:
Формула (4.88) описывает происходящие во всей области колебания, амплитуда которых различна в различных точках. На рисунке 4.15 представлен график зависимости амплитуды от координаты х.
График показывает, что имеются точки, в которых амплитуда колебаний обращается в нуль. Эти точки называются узлами. Имеются также точки, в которых амплитуда достигает максимального значения 2А. Эти точки называются пучностями. Расстояние между соседними узлами и соседними пучностями одинаково, оно равно половине длины волны. Из формулы (4.88) видим, что колебания в промежутке между соседними узлами происходят в одной фазе, но при переходе через узел фаза колебаний меняется на величину представлен график зависимости амплитуды π. В стоячей волне происходит обмен энергией между узлами, где она кинетическая, и соседними с ними пучностями, где она превращается в потенциальную энергию силы упругости. Средний поток энергии в любом сечении волны равен нулю.
Получение электромагнитных волн. Волновое уравнение для электромагнитного поля. Плоская электромагнитная волна. Энергия и импульс, переносимые электромагнитной волной.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.158.197 (0.009 с.) |


 расстояние
расстояние  , а вторая в среде с показателем преломления
, а вторая в среде с показателем преломления  расстояние
расстояние  . Если в точке О фаза колебаний
. Если в точке О фаза колебаний  (
( ), то первая волна возбждает в точке Р колебание
), то первая волна возбждает в точке Р колебание , а вторая
, а вторая 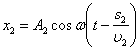 ,
, ,
, 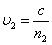 – фазовые скорости первой и второй волны. Следовательно, разность фаз возбуждаемых волнами колебаний в точке Р равна:
– фазовые скорости первой и второй волны. Следовательно, разность фаз возбуждаемых волнами колебаний в точке Р равна: .
. , получим выражение для разности фаз двух когерентных волн:
, получим выражение для разности фаз двух когерентных волн: ,
, – оптическая разность хода, L – оптическая длина пути, s – геометрическая длина пути.
– оптическая разность хода, L – оптическая длина пути, s – геометрическая длина пути. ,
,
 , и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в одинаковой фазе. Следовательно, (8.1.3) является условием интерференционного максимума.
, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в одинаковой фазе. Следовательно, (8.1.3) является условием интерференционного максимума. ,
,
 , и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в противофазе. Следовательно, (8.1.4) является условием интерференционного минимума. Если в какой-либо области пространства распространяются одновременно несколько волн, то в каждой точке происходит сложение нескольких колебаний. Это может привести к явлению интерференции, когда в различных точках интенсивность результирующей волны окажется различной, возникнут максимумы и минимумы интенсивности. Условиями наблюдения интерференции являются совпадение направлений колебания в накладывающихся волнах, равенство частот колебаний и постоянство разности фаз во всех точках наложения. Волны, удовлетворяющие этим условиям, называются когерентными. При наложении когерентных волн квадрат амплитуды результирующих колебаний в каждой точке определяется формулой (4.9)
, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в противофазе. Следовательно, (8.1.4) является условием интерференционного минимума. Если в какой-либо области пространства распространяются одновременно несколько волн, то в каждой точке происходит сложение нескольких колебаний. Это может привести к явлению интерференции, когда в различных точках интенсивность результирующей волны окажется различной, возникнут максимумы и минимумы интенсивности. Условиями наблюдения интерференции являются совпадение направлений колебания в накладывающихся волнах, равенство частот колебаний и постоянство разности фаз во всех точках наложения. Волны, удовлетворяющие этим условиям, называются когерентными. При наложении когерентных волн квадрат амплитуды результирующих колебаний в каждой точке определяется формулой (4.9) ,
, . (4.86)
. (4.86) , (4.87)
, (4.87) ;
;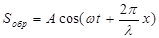 .
.
 . (4.88)
. (4.88)



