
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение Максвелла- БольцманаСодержание книги
Поиск на нашем сайте
Распределение М. и Б. можно объединить в один закон – М-Б, согласно которому число молекул, компоненты скорости которых лежат в интервале от vx, vy, vz до vx+dvx….., а координаты в пределах от x, y, z до x+dx,….. равно: dN(vx, vy, vz, x,y,z) = Aexp(-(U+mv2/2)/kT) dvxdvydvzdxdydz; А – нормировочный множитель, равный Здесь внутренняя энергия U и Екин = mv2/2 могут принимать непрерывный ряд значений.
Б-20 1. Полная механическая энергия частицы. Т.о. приращение кинетической энергии частицы равно элементарной работе Работа всех этих сил идет на изменение приращения кинетической энергии частицы
Известно также, что работа консервативных сил поля равна убыли потенциальной энергии частицы.
Т.о. работа сторонних сил идёт на приращение величины
т.е. приращение полной механической энергии частицы на некотором пути равно работе сторонних сил, действующих на частицу на этом пути; Если Пример: Тело, падающее с обрыва
2. Равенство поперечных размеров тел и лоренцево сокращение. Лоренцево сокращение, Фитцджеральдово сокращение, также называемое релятивистским сокращение длины движущегося тела или масштаба — предсказываемый релятивистской кинематикой эффект, заключающийся в том, что с точки зрения наблюдателя движущиеся относительно него предметы имеют меньшую длину (линейные размеры в направлении движения), чем их собственная длина. Множитель, выражающий кажущееся сжатие размеров, тем сильнее отличается от 1, чем больше скорость движения предмета. Эффект значим только если скорость предмета по отношению к наблюдателю сравнима со скоростью света. Пусть стержень длины l движется (вдоль своей длины) со скоростью v относительно некой системы отсчёта. В таком случае в фиксированный момент времени расстояние между концами стержня составит
Величина, обратная ко множителю с корнем называется также Лоренц-фактором. С её использованием эффект можно сформулировать и так: время пролёта стержня мимо фиксированной точки пространства составит
При этом, все размеры поперёк движения не меняются. 3. Средние скорости молекул: арифметическая, квадратичная, наиболее вероятная. Пользуясь функцией распределения М., можно вычислить ряд важных в молекулярной физике величин: средней арифметической скорости <v>, средней квадратичной скорости 1. Средняя арифметическая скорость <v> по определению равна отношению суммы скоростей всех молекул единицы объема к числу молекул единицы объема. Число молекул в единице объема dnv, скорости которых заключены в интервале от v до v+dv равно nf(v)dv; Сумма скоростей всех таких молекул равна vnf(v)dv. Чтобы найти сумму скоростей всех молекул, обладающих любыми скоростя
<v> = ∫vf(v)dv, подставив f(v), получим:
vdv = d(v2)/2, значит <v> = 4/√π (m/2kT)3/2½∫ v2e d(v2) Введем новую переменную Z=mv2/2kT: ½∫ v2e d(v2) = ½ (2kT/m)2∫Ze-ZdZ, тогда, учитывая, что ∫Ze-ZdZ =1, получим: <v> = 4/√π (m/2kT)3/22(kT/m)2 = √8kT/πm 2. Средняя квадратичная скорость √<v2> – отношение суммы квадратов скоростей молекул единицы объема к числу молекул в этом объеме: <v2> = ∫ v2f(v)dv = 4π(m/2πkT) 3/2∫ v4e dv берется по частям ∫ v4edv = 3/8(2kT/m)5/2√π тогда <v2> = 3kT/m; = √<v2> = √3kT/m 3. Наиболее вероятная скорость молекулы, ей соответствует max на кривой распределения М., поэтому ее находят, приравнивая производную функции нулю: (d/dv)f(v) = d/dv[4/√ т.е. d/dv(v2e) = 0, после дифференцирования получаем: 2ve(1-mv2/2kT) = 0. Это уравнение имеет три решения: v = 0; v = ∞, либо выражение в скобках равно нулю. Следовательно, vн находят из условия: 1- mv2/2kT = 0 => vн = √2kT/m Сравнивая выражения для <v>, vср. кв. = √3π/8<v> = 1,13<v> = √3/2 vн = 1,22vн т.е. и средняя арифметическая, и средняя квадратичная скорости близки к vн.
Б.21 1. Закон сохранения механической энергии частицы. Из выражения Если сторонние силы отсутствуют, то полная механическая энергия частицы в стационарном поле консервативных сил остается постоянной.
Закон сохранения позволяет решать многие вопросы, не привлекая уравнения движения, которые часто приводят к??? расчетам. 2. Преобразования Лоренца. Преобразованиями Лоренца в физике, в частности в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты Чтобы явно различить преобразования Лоренца со сдвигами начала отсчёта и без сдвигов, когда это необходимо, говорят о неоднородных и однородных преобразованиях Лоренца. Преобразования Лоренца без сдвигов начала отсчёта образуют группу Лоренца, со сдвигами — группу Пуанкаре, иначе называемую неоднородной группой Лоренца. С математической точки зрения преобразования Лоренца — это преобразования, сохраняющие неизменной метрику Минковского, то есть, в частности, последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой (другими словами преобразования Лоренца — это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса к другому, то есть аналог поворота координатных осей для пространства-времени). В математике или теоретической физике преобразования Лоренца могут относиться к любой размерности пространства. Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени. Следует заметить, что лоренц-ковариантны не только фундаментальные уравнения (такие, как уравнения Максвелла, описывающее электромагнитное поле, уравнение Дирака, описывающее электрон и другие фермионы), но и такие макроскопические уравнения, как волновое уравнение, описывающее (приближенно) звук, колебания струн и мембран, и некоторые другие (только тогда уже в формулах преобразованияй Лоренца под c следует иметь в виду не скорость света, а какую-то другую константу, например скорость звука). Поэтому преобразования Лоренца могут быть плодотворно использованы и в связи с такими уравнениями (хотя и в довольно формальном смысле, впрочем, мало отличающемся - в своих рамках - от их применения в фундаментальной физике). Если ИСО K' движется относительно ИСО K с постоянной скоростью V вдоль оси x, а начала пространственных координат совпадают в начальный момент времени в обеих системах, то преобразования Лоренца (прямые) имеют вид:
где c — скорость света в вакууме, величины со штрихами измерены в системе K', без штрихов — в K.
3. Обратимые и необратимые термодинамические процессы. Для расширения представлений о термодинамических процессах уточним понятие обратимого процесса: процесс, совершаемый системой наз. обратимым, если после него можно возвратить систему и все тела, взаимодействующие с ней, в их начальное состояние таким образом, чтобы в других телах не возникало каких-либо остаточных изменений. Необходимое условие обратимости терм. процесса – его равновесность, т.е. всякий обратимый процесс всегда является равновесным (квазистат). Однако не всякий равновесный процесс является обратимым. Например, квазистататический процесс равномерного движения по поверхности под действием силы тяжести и трения – процесс необратимый. Пример обратимого процесса – незатухающие колебания тела, подвешенного на пружине в вакууме. Система тело-пружина консервативна. Ее механические колебания не вызывают никаких изменений в энергии теплового движения частиц системы. Изменение состояния системы связано с изменением ее конфигурации и скорости движения тела, которые полностью повторяются через период. Пример необратимого процесса – торможение тела под действием силы трения. Если сила трения единственная сила, то скорость тела уменьшается и оно останавливается. При этом энергия мех движ. тела, как целого уменьш. и расходуется на увел. энергии тепл. движ. частиц тела и среды. Другими словами, за счет нач. кинет. эн. тела (Wк) растет внутрення энергия U тела и среды, нагревающихся при трении ΔU = Wк. Этот прямой процесс протекает самопроизвольно, он идет без каких либо процессов, происходящих с окружающими телами. Но для осуществления обратного процесса возвращения системы в исходное состояние необходимо, чтобы остановившееся тело вновь пришло в движение за счет энергии, выделившейся при его охлаждении и окружающей среды. Известно, что хаотическое движение тела, т.е., U не может самопроизвольно привести к упорядоченному движению всех частиц тела, как целого. Для реализации этого необходим дополнительный, так называемый компенсирующий процесс. Он заключается в охлаждении тела и окружающей среды до первоначальной Т, т.е., в отдаче ими некоторому другому телу теплоты Q = Wк и в совершении над рассматриваемым телом работы, равной Wк. Поэтому, хотя в результате прямого и обратного процесса система тело-среда возвратилась в исходное состояние, состояние внешних тел изменяется (меняется Т, затем совершается работа, т.е. меняются координаты). Следовательно, процессы сопровождающиеся трением необратимы. Процесс теплообмена между двумя телами с разной Т приводит к выравниванию средних энергий тепл. движения частиц обоих тел. Энергия частиц более нагретого тела уменьшается, менее нагретого – увеличивается. В итоге Т1 = Т2. Процесс идет самопроизвольно, как только обеспечен контакт между телами. Обратный процесс – нагревание одного тела за счет охлаждения другого, имевшего вначале Т1 = Т2, самопроизвольно не протекает. Для него используется холодильное устройство, работа которого приводит к изменению состояния других внешних тел. Значит процесс теплообмен при конечной ΔТ является необратимым. Можно показать, что необратимыми являются процессы диффузии и растворения. Из всех этих примеров необратимых процессов можно сделать общие выводы: Все они в прямом направлении происходят самопроизвольно, а для осуществл. обр. проц. требуется одновременное протекание компенсирующих процессов. Все реальные процессы идут с конечной скоростью и сопровождаются трением и теплообменом при конечной разности температур тел, находящихся в тепловом контакте, значит все реальные процессы, строго говоря, необратимы. Однако в некоторых случаях условия протекания процесса таковы, что их приближенно можно считать обратимыми.
Б-22 1. Кинематика вращательного движения: угол поворота, угловая скорость, угловое ускорение, связь между линейной и угловой скоростью.
 называется угловой скоростью тела направлена вдоль оси вращения, в сторону, определяемую правилом правого винта — тоже псевдовектор, модуль называется угловой скоростью тела направлена вдоль оси вращения, в сторону, определяемую правилом правого винта — тоже псевдовектор, модуль  , если , если  — равномерное вращение — равномерное вращение  , для равномерного движения , для равномерного движения  -угол поворота в единицу времени. -угол поворота в единицу времени. 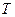 период вращения период вращения  число оборотов число оборотов  , а , а  . .
Понятия Вектор
Точки вращающегося тела имеют разные линейные скорости, которые определяют Найдем связь между векторами Модуль нормального ускорения точек Когда ось вращения не поворачивается в пространстве, тогда тангенциальное ускорение:
Т.о. нормальное и тангенциальное ускорение растут пропорционально 2. Релятивистский импульс. Основное уравнение релятивистской механики. Уравнение Вектор В форме (**) основной закон динамики материальной точки утверждает, что скорость изменения импульса материальной точки равна действующей на нее силе. В этом состоит (согласно современной терминологии) второй закон Ньютона. Основной закон динамики материальной точки выражает принцип причин в классической механике, т.к. устанавливает однозначную связь между изменением со временем состояния движения и положения материальной точки в пространстве и действия на нее силы. Закон позволяет по начальному состоянию точки ( На основании обобщения опытных фактов был установлен важный принцип независимости действия сил: если на материальную точку одновременно действует несколько сил, то каждая из них, сообщает материальной точке такое же ускорение, как если бы других сил не было. Т.о.
Основной закон можно переписать в виде:
вектор
 —импульс силы; —импульс силы;
если 3. Энтропия. Энтропия идеального газа. Энтропия (от греческого слова преобразовать, превращать) В середине ХІХ века было сделано существенное открытие, касающееся обратимых т. процессов. Это открытие связано с именами Карно и Клаузиуса и является существенной частью 2-го закона термодинамики. Оказалось, что наряду с внутренней энергией у тела имеется еще одна важная функция состояния – энтропия. Так же, как и внутренняя энергия, энтропия определяется с точностью до произвольной постоянной. В опытах проявляется значение разности энтропий. Если тело или система при бесконечно малом переходе из одного состояния в другое при температуре Т получает малое количество теплоты δQ, то отношение δQ/Т является полным дифференциалом некоторой функции S. Эта функция и есть энтропия, определяющаяся, таким образом равенством: dS = δQ/Т, при малом переходе, а для конечного изменения: ΔS = S2-S1 = Сущность энтропии заключается в следующем: Переход системы из одного состояния в другое может произойти бесчисленным количеством способов (разные кривые на графике с окончанием в одних 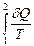 будет иметь одинаковое значение, т.е., не зависит от вида перехода, а определяется только состояниями системы в точках 1 и 2. Значит S является функцией состояния. будет иметь одинаковое значение, т.е., не зависит от вида перехода, а определяется только состояниями системы в точках 1 и 2. Значит S является функцией состояния.
Например, тело нагревают равномерно от 20 до 25˚С, при этом оно получает по 5 Дж теплоты на 1 К. Тогда прирост энтропии, примерно, равен S2-S1 ≈ Наиболее просто выразить изменение энтропии при изотермическом процессе: S2-S1 =
За нуль энтропии может быть принято значение энтропии любого состояния, (кипящей воды, плавящегося льда). Однако, в некоторых случаях за нуль S =
Если известно уравнение состояния вещества, то энтропия (с точностью до const) может быть вычислена весьма просто. По определению: dS = δQ/Т, подставив сюда δQ из 1-го з-на т. получим: dS = (m/M)(CvdT/T+RdV/V) Взяв определенный интеграл, получим S2-S1 = (m/M)(Cv lnT2 /T1+ RlnV2/V1). Это выражение для энтропии идеальных газов: она возрастает с повышением Т и при увеличении объема газа при подводе к нему теплоты δQ.
Б-23 1. Нормальное ускорение и модуль тангенциального ускорения при вращении. Движение точки характеризуется также ускорением—быстротой изменения скорости
т.е. вектор
где Если траектории точки плоская кривая, то можно выбрать два перпендикулярных направления: касательная к траектории (орт Т.к. вектор скорости направлен по касательной к траектории в сторону её движения, то
тогда
и ускорение точки 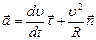 ; ;
Нормальное ускорение
При ускоренном движении
2. Кинетическая энергия релятивистской частицы.
 движется пол действием силы движется пол действием силы  . Элементарная работа этой силы: . Элементарная работа этой силы:  ; ( ; ( ) )    . Скалярное произведение . Скалярное произведение  ; ;  — проекция вектора приращения скорости — проекция вектора приращения скорости  на направление вектора на направление вектора  . Она равна . Она равна  — приращению модуля вектора скорости, тогда — приращению модуля вектора скорости, тогда  и работа и работа  . Отсюда видно, что работа результирующей силы . Отсюда видно, что работа результирующей силы  идет на приращение некоторой физической величины идет на приращение некоторой физической величины  , которую называют кинетической энергией и которая является мерой энергии движения материальной точки. , которую называют кинетической энергией и которая является мерой энергии движения материальной точки.
При конечном перемещении из т.1 в т.2
Т.е. приращении кинетической энергии частицы при перемещении из т.1 в т.2 равно алгебраической сумме работ всех сил, действующих на частицу на этом перемещении. Если 3. Принцип возрастания энтропии. Примеры: при теплообмене, при расширении в вакуум, при механическом движении в сосуде с газом. Необратимость всех реальных процессов в конечном счете связана с тем, что в каждом из них присутствует один из самопроизвольных процессов. В реальных явлениях невозможно избежать ни самопроизвольного расширения, ни трения, ни теплового рассеяния. Во всем этом есть один общий признак. Он состоит в том, что во всех самопроизвольных процессах энтропия возрастает. Примеры: а) При теплообмене между двумя телами с разными температурами общее изменение энтропии равно: S2-S1 = Q1/Т1+ Q2/Т2, где Q1 – тепло полученное, холодным телом; Q2 – тепло, отданное горячим телом. т.к. Т2> Т1 то Q1 = - Q2>0 - тепло, отданное телом, считается <0, тогда S2-S1 = Q1(1/ Т1-1/ Т2)>0, т.е., при теплообмене общая энтропия системы возрастает. б) Если внутри сосуда с газом происходит интенсивное механическое движение (вертится колесо), то температура газа за счет внутреннего трения растет (при этом V = const), поэтому энтропия системы изменится: S2-S1 = (m/M)(CvlnT2/T1), т.е., снова возрастает. в) При расширении газа в пустоту при Т = const приращение энтропии: S2-S1 = (m/M)(RlnV2/V1); опять >0. Итак, во всех самопроизвольных процессах энтропия системы возрастает. Это имеет важное значение для необратимых процессов. Для обратимых процессов прирост энтропии был бы равен dS = δQ/T; Т.к. каждый необратимый процесс сопрово |
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.015 с.) |

 .
. всех сил, действующих на частицу. Если частица находится в стационарном поле консервативных сил, то на нее действует консервативная сила
всех сил, действующих на частицу. Если частица находится в стационарном поле консервативных сил, то на нее действует консервативная сила  со стороны поля. кроме этого на неё могут действовать и другие силы
со стороны поля. кроме этого на неё могут действовать и другие силы  ; т.е. результирующая сила
; т.е. результирующая сила  .
.
 , значит
, значит  или
или 
 . Эту величину называют полной механической энергией частицы в поле
. Эту величину называют полной механической энергией частицы в поле  . Отсюда видно, что
. Отсюда видно, что  определяется с точностью до постоянной, так как с точность до
определяется с точностью до постоянной, так как с точность до  определяется
определяется  . Теперь можно записать
. Теперь можно записать (***)
(***) , то полная механическая энергия частицы растёт при
, то полная механическая энергия частицы растёт при  , — уменьшается.
, — уменьшается. .
. , где c — скорость света.
, где c — скорость света. .
.
 v = √<v2> и наиболее вероятной скорости vн.
v = √<v2> и наиболее вероятной скорости vн. <v> = 4/√π
<v> = 4/√π  (m
(m  /2kT)3/2∫ v3e dv = 4/√π (m/2kT)3/2∫ v2e vdv
/2kT)3/2∫ v3e dv = 4/√π (m/2kT)3/2∫ v2e vdv
 v и vн, видно, что
v и vн, видно, что следует, что в стационарном поле консервативных сил полная механическая энергия частицы может изменяться под действием только сторонних сил, отсюда вытекает закон сохранения механической энергии частицы.
следует, что в стационарном поле консервативных сил полная механическая энергия частицы может изменяться под действием только сторонних сил, отсюда вытекает закон сохранения механической энергии частицы. ;
; 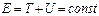
 каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.
каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.



 Поворот тела на некоторый угол
Поворот тела на некоторый угол  можно задать в виде отрезка длина которого
можно задать в виде отрезка длина которого  При поворотах на очень малые углы, путь проходимый точкой можно считать прямолинейным, поэтому два последовательных малых поворота
При поворотах на очень малые углы, путь проходимый точкой можно считать прямолинейным, поэтому два последовательных малых поворота  и
и  (вокруг разных осей, оси
(вокруг разных осей, оси 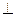 в данном случае) обуславливают как видно из рис., такое же перемещение,
в данном случае) обуславливают как видно из рис., такое же перемещение,  любой точки тела, как и поворот
любой точки тела, как и поворот  получаемый из
получаемый из  , связывается с направлением вращения тела, следовательно
, связывается с направлением вращения тела, следовательно  не является истинным вектором, а является псевдовектором.
не является истинным вектором, а является псевдовектором.

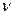 можно сохранить и для неравномерного вращения, понимая под ними мгновенное вращение.
можно сохранить и для неравномерного вращения, понимая под ними мгновенное вращение. может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве (по направлению). Если за
может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве (по направлению). Если за 
 то изменение угловой скорости со временем характеризуется угловым ускорением
то изменение угловой скорости со временем характеризуется угловым ускорением
 — тоже псевдовектор.
— тоже псевдовектор.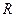 . Если за
. Если за  . Линейная скорость точки
. Линейная скорость точки  ; т.е.
; т.е. 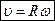 .
. и
и  . Из рис. видно, что
. Из рис. видно, что  совпадает с
совпадает с  равен
равен  .
. или через
или через 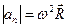 .
. ;
;  -модуль угловой скорости, т.е
-модуль угловой скорости, т.е  .
. описывает изменение движения протяженного тела под действием силы при отсутствии деформации и оно движется. Для точки оно справедливо всегда. поэтому его можно рассматривать как основной закон движения материальной точки: ускорение материальной точки пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. В механике Ньютона масса не зависит от характеристик движения,
описывает изменение движения протяженного тела под действием силы при отсутствии деформации и оно движется. Для точки оно справедливо всегда. поэтому его можно рассматривать как основной закон движения материальной точки: ускорение материальной точки пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. В механике Ньютона масса не зависит от характеристик движения,  ,
,  ускорение
ускорение  ;
;  или
или 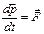 (**).
(**). называют импульсом материальной точки. В теоретической механике(а раньше и в физике) вектор
называют импульсом материальной точки. В теоретической механике(а раньше и в физике) вектор  называют количеством движения. Импульс одна из важнейших динамических характеристик материальной точки
называют количеством движения. Импульс одна из важнейших динамических характеристик материальной точки ) и действующей силы рассчитать состояние материальной точки в любой последующий момент времени.
) и действующей силы рассчитать состояние материальной точки в любой последующий момент времени. ;
;  ;
; называется элементарным импульсом силы за малый промежуток времени
называется элементарным импульсом силы за малый промежуток времени  её действия. Т.о. из основного закона и принципа независимости действия сил следует, что изменение импульса материальной точки за малый промежуток времени
её действия. Т.о. из основного закона и принципа независимости действия сил следует, что изменение импульса материальной точки за малый промежуток времени  Изменение импульса за конечный промежуток времени от
Изменение импульса за конечный промежуток времени от  до
до 

 то
то  ,
,  среднее значение силы за
среднее значение силы за  δQ/Т
δQ/Т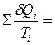 5/293,5+5/294,5+5/295,5+5/296,5+5/297,5 Дж/К.
5/293,5+5/294,5+5/295,5+5/296,5+5/297,5 Дж/К. =Q/Т, т.к., Т = const. Пример: при таянии 1 кг льда
=Q/Т, т.к., Т = const. Пример: при таянии 1 кг льда Дж/К.
Дж/К. νСрdT/T если нагрев происходил при р= const. Чтобы определение энтропии dS = δQ/Т было обоснованным, необходимо доказать, что в любом обратимом круговом процессе интеграл от δQ/Т тождественно равен 0.
νСрdT/T если нагрев происходил при р= const. Чтобы определение энтропии dS = δQ/Т было обоснованным, необходимо доказать, что в любом обратимом круговом процессе интеграл от δQ/Т тождественно равен 0. δQ/Т ≡0, т.е. S = const
δQ/Т ≡0, т.е. S = const ;
; 
 равен производной
равен производной  совпадает с направлением приращения скорости
совпадает с направлением приращения скорости  , то ускорение точки равно второй производной по времени от радиус-вектора:
, то ускорение точки равно второй производной по времени от радиус-вектора: ;
;  ;
;  ;
; —проекция.
—проекция. ) и нормали к ней
) и нормали к ней 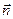 . Тогда
. Тогда  .
. ;
; ;
; ;
; 
 ;
;  —приращение орта касательной к траектории, соответствующее элементарному пути
—приращение орта касательной к траектории, соответствующее элементарному пути  за
за  Ввиду малости
Ввиду малости  его можно считать совпадающим с дугой окружности радиуса
его можно считать совпадающим с дугой окружности радиуса  .
. Соответственно, единичный вектор
Соответственно, единичный вектор  . Из равнобедренного треугольника
. Из равнобедренного треугольника  , ввиду малости
, ввиду малости  совпадает с
совпадает с 
 )
) ;
; — касательное(тангенциальное) ускорение характеризует быстроту изменения модуля скорости. При ускоренном движении
— касательное(тангенциальное) ускорение характеризует быстроту изменения модуля скорости. При ускоренном движении  и
и  совпадает с
совпадает с  и
и  характеризует быстроту изменения направления вектора скорости. Направлено к центру кривизны траектории;
характеризует быстроту изменения направления вектора скорости. Направлено к центру кривизны траектории;  ; поэтому его называют центростремительным. При прямолинейном движении
; поэтому его называют центростремительным. При прямолинейном движении  .
. Модуль ускорения
Модуль ускорения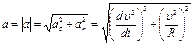 ;
; то
то  касательной
касательной



 , т.о.
, т.о.  (*)
(*) ;
;  (**)
(**) то
то  — кинетическая энергия растет. Если
— кинетическая энергия растет. Если  — уменьшается (силы трения). Уравнения (*, **) справедливы в инерциальных и неинерциальных системах отсчета. А в последних, необходимо в работу всех сил учитывать работ сил инерции.
— уменьшается (силы трения). Уравнения (*, **) справедливы в инерциальных и неинерциальных системах отсчета. А в последних, необходимо в работу всех сил учитывать работ сил инерции.


