
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Консервативный гармонический осцилляторСодержание книги
Поиск на нашем сайте
Второй закон Ньютона для такого осциллятора запишется в виде:
Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид:
где A,φ произвольные постоянные, которые определяются из начальных условий. Найдем частное решение. Для этого подставим в уравнение решение вида:
Тогда окончательное решение запишется в виде:
Из анализа этого решения видно, что при частоте вынуждающей силы равной частоте свободных колебаний возникает резонанс, то есть «неограниченный» линейный рост амплитуды со временем. Из курса математического анализа известно, что решение в этом случае надо искать в виде:
Таким образом колебания в резонансе будут описываться следующим соотношением:
3. Изопроцессы идеального газа: изотермический. Изотермический процесс, Т=const. (закон Бойля – Мариотта) Может происходить в условиях, когда теплообмен между газом и внешней средой осуществляется при постоянной (конечной) разности температур. Для этого теплоемкость внешней среды должна быть велика и процесс расширения или сжатия должен идти весьма медленно (для квазиравновесия). Изотермическими являются процессы кипения, конденсации, плавления и кристаллизации химически чистых веществ, происходящих при постоянном давлении. Для идеального газа в этом процессе выполняется закон Бойля – Мариотта:
т.е., вся теплота, сообщенная системе, идет на совершение газом работы против внешних сил:
При изотермическом расширении Теплоемкость газа в изотермическом процессе
Б-11 1. Закон сохранения импульса системы. Рассмотрим систему состоящую из 2 частиц, на которые действуют также силы Нам известно, что
Значит для двух частиц:
Суммарный момент внутренних сил относительно любой точки равен 0. силы взаимодействия между частицами Закон справедлив и в неинерциальной системе отсчета в тех случаях когда суммарный момент всех внешних сил, включая силы инерции равен нулю.
Момент импульса
В физике понятие момента импульса расширяют на немеханические системы (с электромагнитным излучением, в атомах, ядра и др.) где не действуют законы Ньютона. Здесь закон сохранения момента импульса уже не является следствием законов Ньютона, а представляет собой самостоятельный принцип, является обобщением опытных фактов и является одним из фундаментальных законов наряду с законами сохранения энергии и импульса. 2. Резонанс. Резонанс — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае вам придётся довольно тяжело. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках). В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора. Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником. Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В тоже время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов. Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы. Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов. Струна Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:
где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:
Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:
где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны. Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты. 3. Изопроцессы идеального газа: адиабатный. Адиабатный процесс, Это процесс, при котором система не обменивается теплотой с окружающей средой. Практически процесс производят при достаточно быстром расширении или сжатии газа. Тогда из первого закона следует:
Здесь теплоемкость при адиабатном процессе - Из (13) видно, что При расширении Связь между параметрами состояния адиабатного процесса можно найти, взяв дифференциалы от
Тогда
Это есть уравнение адиабаты или уравнение Пуассона. С помощью уравнения Менделеева – Клапейрона его можно записать через другие параметры:
Из рис. видно, что адиабата идет круче, чем изотерма, поскольку Работа в адиабатном (конечном) процессе 1-2 (на рис. площадь под кривой)
Б-12 1. Энергия и работа. Элементарная работа и работа.
Действие силы на перемещении
 Значит элементарная работа Значит элементарная работа  (*) (*)
Суммируя (интегрируя) по всем элементарным участкам пути от 1 к 2 найдем работу силы
Геометрический смысл этого выражения виден из рисунка
Найдем для примера работу некоторых центральных сил. 1.
 ; ;  —орт радиус вектора —орт радиус вектора  . Элементарная работа не???? . Элементарная работа не???? 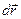 : :  ; ;  — приращение модуля вектора — приращение модуля вектора  ; ;  . .
2.
 ; ;  — радиус вектор частицы М относительно точки О. элементарная работа — радиус вектор частицы М относительно точки О. элементарная работа  ; ; 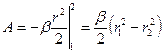 . .
3. Работа сил тяжести. Работа всех этих сил не зависит от формы пути а только от положения точек 1,2. Эта особенность не всех сил. Силы трения не обладают таким свойством. 2. Распространение волн в упругой среде. Волновой фронт. Волновая поверхность. 3. Характер теплового движения молекул. Если газ находится в равновесии, его молекулы движутся совершенно хаотически. Все направления движения равновероятны, ни одному из них не может быть отдано предпочтение, из-за этого молекулы будут равномерно распределены по объему. Скорости молекул могут быть самыми различными по величине. При каждом соударении с другой молекулой скорость данной молекулы может, как возрасти, так и уменьшиться с равной вероятностью. Изменение v молекулы происходит случайным образом. Скорость молекулы не может быть равной бесконечности, а также равной 0. Следовательно, очень малые и очень большие скорости молекул по сравнению со средней скоростью <v> маловероятны; скорости молекул группируются в основном вблизи некоторого наиболее вероятного значения скорости. Например, линейный размер молекулы кислорода» 4 А, объем 10-23 см3. При нормальных условиях на одну молекулу приходится объем» 0,4×10-19 см3. Т.е., молекулы встречаются редко, проходя путь» 1000А между столкновениями. Т.к. скорость молекул велика, примерно 500 м/с, столкновения происходят через 10-10 с. Удары о стенки сосуда ничего не меняют, т.к. скорость изменяется только по направлению. Молекулы притягиваются, когда расстояние между ними имеет порядок их размеров. Значит, большую часть пути они движутся прямолинейно и равномерно. Время взаимодействия очень мало» 10-13 с, т.е., взаимодействие можно считать соударением. Большую часть «своей жизни» молекула проводит в свободном движении по инерции. Хаотичность движения молекул наглядна, если взять сферу некоторого произвольного радиуса r с центром в т. О. Любая т. А на сфере определяет направление от О к А. След-но направление движ. мол. в нек. момент времени м.б. задан. точками на сфере. Равновероятность всех напр. приводит к тому, что точки, изображающие напр. движ. мол., распределяется по сфере с пост. плотностью, равной числу мол. N/4πr2. Соударения приводит к измен. направлений движ. мол., поэтому положение N точек на сфере неопред. меняются, однако плотность точек из-за хаотичности движ. остается пост. Можно найти какое кол-во мол. движется в напр., близких к данному (А). Таким напр. соответствуют все точки элемента пов. ΔS в окрестности т.А. В пределах ΔS будет (*) ΔNA = N(ΔS/4πr2) = NΔΩ/4π ΔΩ тел угол, в кот. закл.напр. Индекс А означает, что имеются ввиду мол. с направл. ≈ А. Направление ОА можно задать с помощью полярного угла θ и азимут угла φ отсчитываемых от напр. ОZ и плоск. Р0. Разделив dS/r2 получим элемент тел. угла, отвечающий инт. углов от θ до θ+dθ и от φ до φ+dφ dΩ = sinθdθdφ Две сферы с r и r+dr, два конуса с углами раствора θ и θ+dθ и две плоскости, образующие с Р0 углы φ и φ+dφ образуют в пр-ве прямоуг. параллелепипед с объемом dV = dSdr = r2sinθdrdθdφ – элемент объема в сферической сист. коорд. (объем, отвечающий приращению корд. r, θ, φ на dr, dθ, dφ) Перейдя от дельт и диффер. в ф-ле (*) и подставив dΩ получим dNv,φ = N(dΩvφ/4π) = Nsinθdθdφ/4π Индексы указывают на то, что имеются в виду молекулы, напр. движ. которых отвечают интервалам углов от θ до θ+dθ и от φ до φ+dφ. Б-13 1. Работа гравитационной силы, упругой силы и силы тяжести.
 ; ;  —орт радиус вектора —орт радиус вектора  . Элементарная работа не???? . Элементарная работа не???? 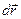 : :  ; ;  — приращение модуля вектора — приращение модуля вектора  ; ;  . .
2.
 ; ;  — радиус вектор частицы М относительно точки О. элементарная работа — радиус вектор частицы М относительно точки О. элементарная работа  ; ; 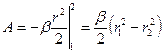 . .
3. Работа сил тяжести. Работа всех этих сил не зависит от формы пути а только от положения точек 1,2. Эта особенность не всех сил. Силы трения не обладают таким свойством. 2. Уравнение плоской и сферической волн. 3. Средняя арифметическая скорость молекулы. Средняя арифметическая скорость <v> по определению равна отношению суммы скоростей всех молекул единицы объема к числу молекул единицы объема. Число молекул в единице объема dnv, скорости которых заключены в интервале от v до v+dv равно nf(v)dv; Сумма скоростей всех таких молекул равна vnf(v)dv. Чтобы найти сумму скоростей всех молекул, обладающих любыми скоростя
<v> = ∫vf(v)dv, подставив f(v), получим:
vdv = d(v2)/2, значит <v> = 4/√π (m/2kT)3/2½∫ v2e d(v2) Введем новую переменную Z=mv2/2kT: ½∫ v2e d(v2) = ½ (2kT/m)2∫Ze-ZdZ, тогда, учитывая, что ∫Ze-ZdZ =1, получим: <v> = 4/√π (m/2kT)3/22(kT/m)2 = √8kT/πm
Б-14 1. Мощность. по определению это работа, выполненная за единицу времени. Если за промежуток времени
Зная
2. Волновое уравнение. Волновое уравнение в математике — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. В общем случае волновое уравнение записывается в виде
где
где
Оператор Д’Аламбера Разность Неоднородное уравнение Допустимо также рассматривать неоднородное волновое уравнение
где f = f(x,t) — некая заданная функция внешнего воздействия (внешней силы). Стационарным вариантом волнового уравнения является, очевидно, уравнение Лапласа (уравнение Пуассона в неоднородном случае). Задача нахождения нормальных колебаний системы, описываемой волновым уравнением, приводит к задаче на собственные значения для уравнения Лапласа, т.е. к нахождению решений уравнения Гельмгольца, получающегося подстановкой
3. Число ударов молекул о стенку и давление газа на стенку. Рассмотрим находящийся в равновесии газ, заключенный в некотором сосуде. Допустим, что молекулы газа движутся только вдоль трех взаимно ┴ направлений. Это можно допустить из-за хаотичности движения молекул. Если в сосуде находится N молекул, то в любой момент времени вдоль каждого из направлений будет двигаться N/3 молекул и половина из них - N/6 вдоль данного направления в одну сторону, а вторая половина - в другую. Следовательно, в интересующем нас направлении по нормали к данному элементу ΔS стенки сосуда движется N/6 молекул, а для единицы объема - Пусть все молекулы движутся с одинаковой средней скоростью <v>. За время Δt элемента стенки ΔS достигают все молекулы, находящиеся в параллелипипеде с площадью основания ΔS и длиной Δν/ΔSΔt = (n/6)<v>. Если отказаться от допущения, что все молекулы движутся с одинаковой скоростью v = <v>, то необходимо выделить в единице объема молекулы, скорости которых лежат в интервале от v до v+dv. Их число -
Δν = Б-15 1. Консервативные силы. Если в каждой точке пространства на частицу, помещенную туда, действует сила, говорят, что частица находится в поле сил, например в поле сил тяжести, гравитационной, кулоновской и т.д. Поле сил может быть постоянным во времени, тогда оно называется стационарным. Стационарное поле в одной системе отсчета м.б. в другой. В стационарном поле сила, действующая на частицу, зависит только от её положения в пространстве. Работа, которую совершает сила поля по перемещению частиц из т.1 в т.2 зависит, в общем случае от формы пути между этими точками, например при действии
К неконсервативным силам относятся силы трения и сопротивления. Работа этих сил зависит от пути между начальным и конечным положением частицы и не равна 0 на замкнутом пути. 2. Энергия волны. Объемная плотность энергии волны. Энергия волн — энергия волн на поверхности океана, используемая для совершения полезной работы — генерации электроэнергии, опреснения воды и перекачки воды в резервуары. Энергия волн — возобновляемый источник энергии. Мощность волнения оценивают в кВт на погонный метр, т.е. в кВт/м. По сравнению с ветровой и солнечной энергией энергия волн обладает гораздо большей удельной мощностью. Так, средняя мощность волнения морей и океанов, как правило, превышает 15 кВт/м. При высоте волн в 2 м мощность достигает 80 кВт/м. То есть, при освоении поверхности океанов не может быть нехватки энергии. Конечно, в механическую и электрическую энергию можно использовать только часть мощности волнения, но для воды коэффициент преобразования выше, чем для воздуха - до 85%. Волновая энергия представляет собой сконцентрированную энергию ветра и, в конечном итоге, солнечной энергии. Мощность, полученная от волнения всех океанов планеты, не может быть больше мощности, получаемой от Солнца. Но удельная мощность электрогенераторов, работающих от волн, может быть гораздо большей, чем для других альтернативных источников энергии. Несмотря на схожую природу, энергию волн принято отличать от энергии приливов и океанских течений. Выработка электроэнергии с использованием энергии волн не является распространенной практикой, в настоящее время в этой сфере проводятся только экспериментальные исследования. Представляет интерес и использование энергии волн для движения судов (движители волновые). 3. Средняя энергия молекул с учетом вращательных и колебательных степеней свободы. Из уравнения состояния идеального газа p=nkT и выражения для давления газа на стенку сосуда р =2/3n<εпост> следует, что <εпост> = 3/2kT (1), откуда можно заключить, что температура есть величина, прямо пропорциональная средней энергии поступательного движения молекул. Поступательно движутся молекулы газа. Молекулы твердых и жидких тел совершают колебания вблизи положений равновесия. Из выражения (1) видно, что <εпост> зависит только от Т и не зависит от массы молекулы. Т.к., <εпост> = <mv2/2> = m<v2>/2, то из сравнения с выражением (1), получим: <v2> = 3kT/m а средняя квадратичная скорость: vср.кв. = √<v2> = √3kT/m. Можно представить <v2> = <v2x>+<v2y>+<v2z> = 3<v2x>, поскольку, все направления движ |
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.198 (0.01 с.) |

 . Если ввести обозначения:
. Если ввести обозначения:  и заменить ускорение на вторую производную от координаты по времени, то получим следующее дифференциальное уравнение:
и заменить ускорение на вторую производную от координаты по времени, то получим следующее дифференциальное уравнение:
 ,
, и получим значение для константы:
и получим значение для константы:

 подставим этот анзац в дифференциальное уравнение и получим, что:
подставим этот анзац в дифференциальное уравнение и получим, что:

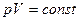 , графиком которого является гипербола, рис.. Внутренняя энергия газа постоянна в процессе, значит:
, графиком которого является гипербола, рис.. Внутренняя энергия газа постоянна в процессе, значит: (11), а
(11), а  ,
, (12)
(12) , к нему подводится теплота
, к нему подводится теплота 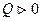 , газ совершает положительную работу,
, газ совершает положительную работу, 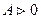 , рис., процесс 1-2. При сжатии газа, процесс 1-3, работа, совершенная газом отрицательна, положительную работу при этом выполняют внешние силы, От газа отводится теплота
, рис., процесс 1-2. При сжатии газа, процесс 1-3, работа, совершенная газом отрицательна, положительную работу при этом выполняют внешние силы, От газа отводится теплота  .
. ± µ, т.к.,
± µ, т.к.,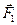 и
и  . Момент импульса является аддитивной величиной. Для системы равен векторной сумме моментов импульса отдельных частиц относительно одной и той же точки
. Момент импульса является аддитивной величиной. Для системы равен векторной сумме моментов импульса отдельных частиц относительно одной и той же точки  .
. —моменту всех сил, действующих на частицу, а изменение момента системы
—моменту всех сил, действующих на частицу, а изменение момента системы 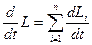 , тогда
, тогда  ;
;  ;
;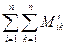 — суммарный момент всех внутренних сил действующих на частицы.
— суммарный момент всех внутренних сил действующих на частицы.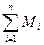 — суммарный момент всех внешних сил действующих на частицы.
— суммарный момент всех внешних сил действующих на частицы. .
. по 3 му закону Ньютона действуют по одной прямой, значит имеют одинаковое плечо, поэтому момент каждой пары внутренних сил равен 0. Т.о.
по 3 му закону Ньютона действуют по одной прямой, значит имеют одинаковое плечо, поэтому момент каждой пары внутренних сил равен 0. Т.о.  ; т.е. системы изменяются под действием внешних сил
; т.е. системы изменяются под действием внешних сил  . Если внешние силы отсутствуют
. Если внешние силы отсутствуют  ,
,  , то
, то 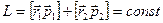 , является аддитивным сохраняющейся величиной. Т.е. момент импульса замкнутой системы частиц остается постоянным, не меняется со временем. Это справедливо относительно любой точки инерциальной системы отсчета:
, является аддитивным сохраняющейся величиной. Т.е. момент импульса замкнутой системы частиц остается постоянным, не меняется со временем. Это справедливо относительно любой точки инерциальной системы отсчета:  т.е. моменты импульса отдельных частей
т.е. моменты импульса отдельных частей 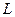 одной части системы происходят за счет убыли
одной части системы происходят за счет убыли  Закон играет такую же роль как закон сохранения энергии импульса. Он позволяет решать разные задачи, не рассматривая детально внутренние процессы. Пример: разгоняют????
Закон играет такую же роль как закон сохранения энергии импульса. Он позволяет решать разные задачи, не рассматривая детально внутренние процессы. Пример: разгоняют???? ;
;  т.е.
т.е.  уменьшается как
уменьшается как 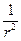 . Этот эффект широко используют гимнасты, фигуристы и т.д. здесь мы интересуемся силами взаимодействия и т.д. у незамкнутых систем может сохраняться не сам
. Этот эффект широко используют гимнасты, фигуристы и т.д. здесь мы интересуемся силами взаимодействия и т.д. у незамкнутых систем может сохраняться не сам  . Это бывает, когда
. Это бывает, когда  всех внешних сил.
всех внешних сил. ;
;  ;
; 
 ,
, ,
,
 ,
, .
. - система совершает работу за счет убыли внутренней энергии. Или, записывая более подробно, получим:
- система совершает работу за счет убыли внутренней энергии. Или, записывая более подробно, получим: (13)
(13) , т.к.,
, т.к.,  (14)
(14)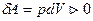 и
и  , газ охлаждается, при адиабатном сжатии
, газ охлаждается, при адиабатном сжатии  и
и  , газ нагревается.
, газ нагревается. и от уравнения Менделеева - Клапейрона:
и от уравнения Менделеева - Клапейрона: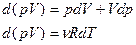 (15), отсюда можно выразить
(15), отсюда можно выразить  , подставить в уравнение (14) и получить:
, подставить в уравнение (14) и получить:  . Заменив здесь
. Заменив здесь  из уравнения Майера, получим после простых преобразований:
из уравнения Майера, получим после простых преобразований: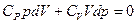 , далее разделим переменные, поделив уравнение на
, далее разделим переменные, поделив уравнение на  и обозначим
и обозначим 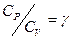 - показатель адиабаты или постоянная Пуассона.
- показатель адиабаты или постоянная Пуассона. . После интегрирования
. После интегрирования  или:
или:
 или
или  .
.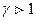 для любого идеального газа. Это объясняется тем, что при адиабатном сжатии увеличение давления происходит не только из-за уменьшения объема, как в изотермическом процессе, но и из-за возрастания температуры. При адиабатном расширении газа его температура уменьшается и давление падает сильнее, чем при соответствующем изотермическом расширении.
для любого идеального газа. Это объясняется тем, что при адиабатном сжатии увеличение давления происходит не только из-за уменьшения объема, как в изотермическом процессе, но и из-за возрастания температуры. При адиабатном расширении газа его температура уменьшается и давление падает сильнее, чем при соответствующем изотермическом расширении.
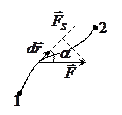 Пусть частица под действием силы
Пусть частица под действием силы  совершает перемещение по некоторой траектории 1-2. в общем случае сила
совершает перемещение по некоторой траектории 1-2. в общем случае сила  .
.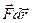 , которое называется элементарной работой силы
, которое называется элементарной работой силы  на перемещении
на перемещении 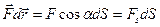 , где
, где  — угол между
— угол между  - элементарный путь
- элементарный путь  проекция вектора
проекция вектора 
 - величина алг. она и
- величина алг. она и  и
и  и = 0 при
и = 0 при  .
. .
. — площадь под прямой. Над осью работа положительна, под — отрицательна.
— площадь под прямой. Над осью работа положительна, под — отрицательна. .
.


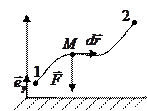
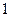

 ;
;  ;
;  — приращение координаты
— приращение координаты  .
. 


 ;
;  .
.


 <v> = 4/√π
<v> = 4/√π  (m
(m  /2kT)3/2∫ v3e dv = 4/√π (m/2kT)3/2∫ v2e vdv
/2kT)3/2∫ v3e dv = 4/√π (m/2kT)3/2∫ v2e vdv сила
сила  , то мощность, развиваемая этой силой в данный момент времени
, то мощность, развиваемая этой силой в данный момент времени  т.е. скалярное произведение
т.е. скалярное произведение  .
. — как и работа величина алгебраическая.
— как и работа величина алгебраическая.




 .
. ,
, — оператор Лапласа,
— оператор Лапласа, 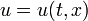 — неизвестная функция,
— неизвестная функция,  — время,
— время,  — пространственная переменная.
— пространственная переменная. ,
, — фазовая скорость.
— фазовая скорость.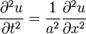 .
.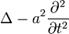 называется оператором Д’Аламбера (разные источники используют разный знак). Таким образом, волновое уравнение записывается как:
называется оператором Д’Аламбера (разные источники используют разный знак). Таким образом, волновое уравнение записывается как: 
 ,
,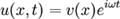 или
или  .
. , n – концентрация молекул.
, n – концентрация молекул. <v>Δt. Их число Δν = (n/6)ΔS<v>Δt, следовательно, число ударов о единичную площадку в единицу времени
<v>Δt. Их число Δν = (n/6)ΔS<v>Δt, следовательно, число ударов о единичную площадку в единицу времени . Количество ударов таких молекул, долетающих до площадки ΔS за время Δt равно dνv = (1/6)(dnvΔ
. Количество ударов таких молекул, долетающих до площадки ΔS за время Δt равно dνv = (1/6)(dnvΔ  dνv = 1/6ΔSΔt
dνv = 1/6ΔSΔt 
 . Однако, имеются стационарные силовые поля, в которых работа над частицей силами поля не зависит от пути между т.1 и т.2. Силы обладающими такими свойствами называются консервативными. Это свойство можно сформулировать другим способом: силы поля являются консервативными, если работа в стационарном полена любом замкнутом пути равна =0.
. Однако, имеются стационарные силовые поля, в которых работа над частицей силами поля не зависит от пути между т.1 и т.2. Силы обладающими такими свойствами называются консервативными. Это свойство можно сформулировать другим способом: силы поля являются консервативными, если работа в стационарном полена любом замкнутом пути равна =0.
 поскольку
поскольку 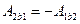 то
то 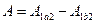 . А т.к. работа не зависит от пути
. А т.к. работа не зависит от пути  , то
, то 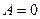 .
.


