Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоемкость идеального газаСодержание книги
Поиск на нашем сайте Из опыта следует, что внутренняя энергия идеального газа зависит только от температуры. Отсутствие зависимости Теплоемкостью какого-либо тела называют величину, равную количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на 1К. Если сообщение телу тепла Теплоемкость единицы массы вещества называют удельной теплоемкостью:
Внутренняя энергия и теплоемкость идеальных газов В идеальном газе молекулы не взаимодействуют между собой, внутренняя энергия одного моля газа: Uм = NA<ε> = i/2 NAkT = i/2 RT. Uм = i/2RT. Если вспомнить, что по определению: Cv = δQ/dT = dU/dT, поскольку, δQ = dU+pdV, а для изохорного процесса dV = 0. Тогда Cv = (i/2) R, а, учитывая, что Cр = Cv+R, получим: Cр = (i+2)/2 R Следовательно, коэффициент Пуассона γ = Cp/Cv = (i+2)/i, таким образом, γ определяется числом и характером степеней свободы молекулы. Согласно этой ф-лы для одноатомной молекулы i = 3 и γ = 1,67; жесткой двухатомной i =5 и γ = 1,4; упругой двухатомной i = 7, а γ = 1,29. В области температур, близких к комнатной, это хорошо согласуется с опытом. Однако, в широком температурном интервале это не так. Оказывается, что вращательная и колебательная энергии молекулы квантованы. При низких Т вращательные и колебательные степени свободы не возбуждены. Молекула Н2 , например, ведет себя как одноатомная в этой области температур, i = 3. В области Т ≈ 500К вращательные степени «разморожены» <ε> > εвращ и молекула Н2 ведет себя как жесткая двухатомная с = 3+2 = 5. При Т>1000К энергии <ε> достаточно для возбуждения колебательной степени свободы, «включены» все степени свободы, i = 7.
Б-17 1. Потенциальная энергия частицы в поле. То обстоятельство, что работа консервативной силы (для стационарного поля) зависит только от начального и конечного положений частицы в поле, позволяет ввести важное физическое понятие потенциальной энергии (функции состояния). Возьмем стационарное поле консервативных сил, например электростатическое поле в котором мы перемещаем частицу (заряд) из разных точек
  (*). (*).
Это значит, что данная работа будет некоторой функцией радиус-вектора
Правая часть представляет убыль потенциальной энергии, т.е. разность начальную и конечную значений потенциальной энергии. ( Однако, как только зафиксирована потенциальная энергия в одной, какой-либо точке, значения её во всех остальных точках поля определяется однозначно выражением (**). Эта формула позволяет найти вид
Отметим еще раз, что потенциальная энергия определяется с точностью до некоторой постоянной величины, что несущественно, т.к. во всех формулах входит разность её значения в двух положениях частицы, поэтому постоянная выпадает, и её опускают. Кроме этого важно заметить, что потенциальную энергию следует относить не к частице в поле а к системе взаимодействующих частиц и тела, создающего поле. При данном характере взаимодействия потенциальная энергия зависит только от положения частицы относительно этого тела. 2. Опыт Майкельсона и Морли. Опыт Майкельсона — физический опыт, поставленный Майкельсоном в 1881 году, с целью измерения зависимости скорости света от движения Земли относительно эфира. Под эфиром тогда понималась среда, аналогичная объёмнораспределённой материи, в которой распространяется свет подобно звуковым колебаниям. Результат эксперимента был отрицательный — скорость света никак не зависела от скорости движения Земли и от направления измеряемой скорости. Позже, в 1887 году Майкельсон, совместно с Морли, провёл аналогичный, но более точный эксперимент, известный как эксперимент Майкельсона-Морли и показавший тот же результат. В 1958 году в Колумбийском университете (США) был проведён ещё более точный эксперимент с использованием противонаправленных лучей двух мазеров, показавший неизменность частоты от движения Земли с точностью около 10−9 % (чувствительность к скорости движения Земли относительно эфира составляла 30 м/с). Ещё более точные измерения в 1974 довели чувствительность до 0,025 м/с. Современные варианты эксперимента Майкельсона [1] используют оптические и криогенные микроволновые резонаторы и позволяют обнаружить отклонение скорости света, если бы оно составляло несколько единиц на 10−16. Опыт Майкельсона является эмпирической основой принципа инвариантности скорости света, входящего в общую теорию относительности (ОТО) и специальную теорию относительности (СТО). 3. Барометрическая формула. Атмосфера, то есть воздушная оболочка Земли, обязана своим существованиям наличию теплового движения молекул и силы притяжения их к Земле. При этом в атмосфере устанавливается вполне определенное распределение молекул по высоте. Соответственно этому, устанавливается определенный закон изменения давления воздуха с высотой, который нетрудно найти. Возьмем вертикальный столб воздуха. Считаем, что при х=0, y поверхности Земли р=р0, а на высоте х давление равно р. При увеличении высоты на dx давление уменьшается на dp. Известно, что давление воздуха на некоторой высоте равно весу вертикального столба воздуха с площадью равной единице, находящегося над этой высотой. Поэтому, dp равно разности весов столбов воздуха с площадью s=1 м2 на высотах x и x+dx, то есть, равно весу столба воздуха высотой dx с площадью основания 1 м2: p-dp-p= -dp= ρgdx ×1 м2, значит, dp= -ρgdx, плотность ρ= m0N/V= m0n, (m0N = m – масса всех молекул). Из молекулярной физики известно, p= nkT => n= p/kT => ρ= m0 p/kT и тогда, подставляя значение плотности, получим: dp= (-m0g/kT)pdx. После разделения переменных: dp/p= (-m0g/kT)dx Считая для простоты температуру постоянной на всех высотах (что не так) после интегрирования найдем: lnp= (-m0g/kT)x +lnC, откуда: p= Ce(-m0g/kT)x. Постоянную C находим из начальных условий: при х= 0 р= р0, то есть р0=C и тогда: р= р0e(-m0g/kT)x или с учетом m0= M/NA: р= р0e(-Mg/RT)x - барометрическая формула, т.е., давление с высотой убывает по экспоненциальному закону. Для градуировки барометров необходимо внести поправки на Т. Так как, давление пропорционально концентрации молекул в единице объема, то: n= n0 e(-mg/kT)x - закон убывания концентрации молекул, а значит, плотности с высотой. Видно, что атмосфера Земли в принципе, простирается до ∞. На больших высотах необходимо учесть, что g – меняется с высотой: g(r)= γM/(r+x)2 .
Б-18 1. Связь между потенциальной энергией и силой для консервативного поля. Взаимодействие частицы с окружающими телами можно описать либо с помощью сил либо с помощью потенциальной энергией. Первый способ более общий, т.к. он применим и к силам, для которых нельзя ввести понятие потенциальной энергии (силы трения). Второй способ удобен тем, что существует связь между потенциальной энергией и силой со стороны поля. Зная эту связь, можно по виду зависимости Найдем эту связь. Известно, что работа консервативных сил при перемещении частицы из одной точки статического поля в другую может быть представлена в виде убыли потенциальной энергии частицы
2. Постулаты Эйнштейна. Специальная теория относительности (СТО) (англ. special theory of relativity; частная тео́рия относи́тельности; релятивистская механика) — теория, описывающая движение, законы механики и пространственно-временные отношения, определяющие их, при скоростях движения, близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей образует общую теорию относительности. Отклонения в протекании физических процессов, описываемые теорией относительности, от эффектов, предсказываемых классической механикой, называют релятивистскими эффектами, скорости, при которых такие эффекты становятся существенными — релятивистскими скоростями. Пусть система отсчёта K' движется со скоростью V относительно системы отсчёта K0, соответственно, штрихованные величины относятся к K', а величины с индексом 0 — к K0. К наиболее распространённым эффектам СТО, также называемым релятивистскими эффектами, относят: Замедление времени Время в движущейся системе отсчёта течёт медленнее:
С этим эффектом связан так называемый парадокс близнецов.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 от объема газа указывает на то, что молекулы идеального газа не взаимодействуют друг с другом, иначе бы во внутреннюю энергию входило слагаемое, зависящее от расстояния между молекулами, т.е., от
от объема газа указывает на то, что молекулы идеального газа не взаимодействуют друг с другом, иначе бы во внутреннюю энергию входило слагаемое, зависящее от расстояния между молекулами, т.е., от 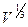 . Значит, подавляющую часть времени молекулы проводят в свободном полете.
. Значит, подавляющую часть времени молекулы проводят в свободном полете.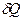 повышает его температуру на
повышает его температуру на  , то теплоемкость тела по определению:
, то теплоемкость тела по определению: 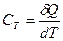 .
.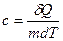 , тогда, молярная теплоемкость:
, тогда, молярная теплоемкость:  , а теплоемкость тела:
, а теплоемкость тела:  .
.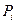 в некоторой фиксированной точке О (точка отсчета). Найдем работу сил поля. Поскольку работа сил поля не зависит от пути, то остаётся зависимость её только от положения т.
в некоторой фиксированной точке О (точка отсчета). Найдем работу сил поля. Поскольку работа сил поля не зависит от пути, то остаётся зависимость её только от положения т.  (О— фиксировано) т.е. от предела интегрирования
(О— фиксировано) т.е. от предела интегрирования точки
точки  . Функцию
. Функцию  называют потенциальной энергией частицы в поле сил. Теперь найдем работу при перемещении частицы из т.1 в т.2. Т.к. она не зависит от формы пути: то
называют потенциальной энергией частицы в поле сил. Теперь найдем работу при перемещении частицы из т.1 в т.2. Т.к. она не зависит от формы пути: то 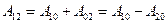 или с учетом (*)
или с учетом (*) ;
; ;
;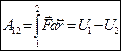 (**)
(**) — приращение); (
— приращение); ( — убыль). Т.о. работа сил Оля на пути 1—2 равна убыли потенциальной энергии. Так как работа сил поля определяется лишь разностью энергий в двух точек, а не их абсолютного значения, то частица в т.О можно приписать любое, наперед выбранное значение потенциальной энергии.
— убыль). Т.о. работа сил Оля на пути 1—2 равна убыли потенциальной энергии. Так как работа сил поля определяется лишь разностью энергий в двух точек, а не их абсолютного значения, то частица в т.О можно приписать любое, наперед выбранное значение потенциальной энергии. для любого стационарного поля консервативных сил. Для этого достаточно вычислить работу совершаемую силами поля между двумя любыми точками и представить её в виде убыли некоторой функции
для любого стационарного поля консервативных сил. Для этого достаточно вычислить работу совершаемую силами поля между двумя любыми точками и представить её в виде убыли некоторой функции  , которая и есть потенциальной энергией. Так и было ране сделано при вычислении работы гравитационной, упругой и силы тяжести. Отсюда видно, что потенциальная энергия частицы в данных полях имеет вид
, которая и есть потенциальной энергией. Так и было ране сделано при вычислении работы гравитационной, упругой и силы тяжести. Отсюда видно, что потенциальная энергия частицы в данных полях имеет вид
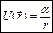 — гравитационная, кулоновская +С – постоянная.
— гравитационная, кулоновская +С – постоянная. — упругой +С
— упругой +С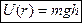 — в поле тяжести.
— в поле тяжести. .
. . Это можно записать и для элементарного перемещения
. Это можно записать и для элементарного перемещения 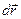 .
.
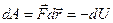

 т.к.
т.к.  ;
;  — элементарный путь или
— элементарный путь или 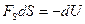 ;
; 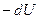 — убыль потенциальной энергии в направлении перемещения
— убыль потенциальной энергии в направлении перемещения  т.е. проекция силы поля
т.е. проекция силы поля  в данной точке на направление перемещения
в данной точке на направление перемещения 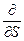 указывает, что произведение берется по определенному направлению. Перемещение
указывает, что произведение берется по определенному направлению. Перемещение  . Если вдоль
. Если вдоль  то
то  ; а
; а  ,
,  — проекция силы
— проекция силы  на орт
на орт  (а не на перемещение
(а не на перемещение  ). Т.о. относительно оси
). Т.о. относительно оси  . Символ
. Символ  означает, что
означает, что  при дифференцировании должна расти как функция одного аргумента
при дифференцировании должна расти как функция одного аргумента  . Значит
. Значит  ;
;  . Зная проекции
. Зная проекции  или
или  . Скобка называется градиент скалярной функции
. Скобка называется градиент скалярной функции  или
или 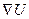 т.о.
т.о.  — символический вектор или оператор Гамильтона.
— символический вектор или оператор Гамильтона.  на скаляр
на скаляр  можно найти
можно найти  .
.