Сокращение линейных размеров

Линейные размеры тел в движущейся системе отсчёта сокращаются:

, для длины.

, для объёма.

Такое сокращение размеров ещё называют лоренцевым сокращением.

«Утяжеление» при ускорении

Релятивистская масса движущегося объекта больше массы покоя:

Однако, в современной физической литературе по СТО m — масса частицы (инвариантная масса) не зависит от скорости, являясь инвариантом относительно преобразований Лоренца, и является величиной неаддитивной. В данной формуле речь идёт о так называемой «релятивистской массе», которая возрастает с увеличением скорости. «Утяжеление» следует понимать лишь условно, как будто справедлив закон Ньютона, а не аналогичный ему закон релятивистской динамики. В современной физической литературе понятие «релятивистской массы» не используется, хотя встречается в ранних работах по теории относительности.

3. Распределение Больцмана.

Барометрическая формула выражает зависимость концентрации молекул газа, находящегося в поле сил тяжести. Величина mgx представляет собой потенциальную энергию молекул на высоте х. Можно также сказать, что формула

n= n₀e^(-m₀ ^g/kT)x

дает нам число частиц n в единице объема, энергия которых равна m₀gx, если концентрация частиц с энергией равной 0 равно n₀ (отсчет х снизу).

Нет оснований считать, что поведение газа изменится, если вместо силы тяжести на него будет действовать какая либо другая сила, тогда для любого силового поля можно сказать,.что число частиц, имеющих заданную потенциальную энергию U, определяется формулой

n= n₀e^-U/kT – формула Больцмана

Она позволяет определить долю частиц, которые в условиях теплового равновесия обладают энергией U:

n/n₀= e^-U/kT

Отсюда видно, что доля n/n₀ частиц с энергией U, т.е., их распределение по энергии определяется (кроме U) температурой. При данной Т доля молекул с той, либо иной энергией зависит от U и быстро уменьшается с ростом энергии. Доля молекул с большой энергией мала. И чем ниже Т, тем быстрее n/n₀ убывает с ростом U, рис.. Чем выше температура, тем равнемернее распределен газ по объему.

Величина n/n₀ в формуле имеет также смысл вероятности n молекул из всего числа n₀ иметь заданную энергию U.

Функция распределения

В уравнение кинетической теории идеальных газов входит средняя кинетическая энергия поступательного движения молекул, которая определяется в свою очередь их средней квадратичной скоростью. Смысл средней квадратичной скорости заключается в том, что это та скорость, которой должны были бы обладать все молекулы (если бы их скорости были одинаковы, а направления равновероятны), чтобы давление было таким, каким оно является на опыте. На самом деле скорости молекул не одинаковы и это учитывалось при выводе основного уравнения молекулярно-кинетической теории. На это указывают и опытные факты, в частности, эксперименты Штерна и Ламмерта. Полоска мишени в этих опытах оказывалась не резкой, а размытой.

Об этом свидетельствует и закон распределения молекул по высоте, то есть, барометрическая формула. Если бы все молекулы имели одинаковую скорость, то распределение было бы иным. Они все поднимались бы до одинаковой высоты mgh = mv²/2 => h= v²/2g, а затем возвращались бы к Земле с первоначальной v, то есть вели бы себя, как брошенное тело. Все молекулы были бы равномерно распределены по высоте, а, значит, атмосфера имела бы резкую границу, чего нет на самом деле.

Благодаря хаотичным движениям молекул и их взаимным столкновениям, молекулы газа каким-то образом распределены по скорости, так, что среди них имеются как очень быстрые, так и очень медленные. Несмотря на хаотичность движений, на случайный характер столкновений и, вызываемых ими изменений скорости молекул, их распределение по скорости, как показывают теория и опыт, оказывается не случайным, не произвольным, а вполне определенным. На его характер не влияют ни столкновения между молекулами, ни даже внешние поля. Оно является однозначным и единственным. И это не только не противоречит представлению о хаотичности молекулярных движений, а именно этим и обусловлено.

При поиске распределения частиц по скорости требуется найти число частиц, скорости которых (или их компоненты v_х, v_y, v_z) лежат в определенном интервале значений скорости (или компонентов скорости). Очевидно, что число ∆n частиц в единице объема, скорости которых лежат в некотором интервале от v до v+∆v, тем больше, чем больше этот интервал, то есть ∆n~∆v или ∆n=k∆v, где k – коэффициент пропорциональности.

Ясно, что ∆n зависит от самой скорости, т. к., в одинаковых интервалах, но для разных значений скорости число частиц будет разное, как не одинаково, например, число людей возраста 99-100 лет и 30-31 года при одинаковом размере интервала – 1 год. Значит коэффициент пропорциональности k зависит от скорости, т.е., k = f(v).

Кроме того, величина Dn должна быть пропорциональна общему числу частиц в единице объема, значит формула для Dn имеет вид: Dn = nf(v) ∆v или ∆n/n = f(v) ∆v. Здесь, ∆n/n – доля частиц в единице объема газа, скорости которых лежат в интервале от v до v+∆v, а f(v) – функция распределения. Задачей статистики является найти её вид. Её смысл ясен из выражения

f(v)= ∆n/n при ∆v=1 м/с

Т.е., это доля частиц, скорости которых заключены в единичном интервале скоростей Dv =1 вблизи скорости v.

Переходя к пределу, т.е. к вероятностям, можно записать:

dn/n=f(v)dv

здесь величина dn/n имеет смысл вероятности того, что любая частица, содержащаяся в единице его объема, имеет скорость в интервале dv вблизи скорости v.

Величине же функции распределения f(v) можно приписать смысл вероятности любой частице в единице объема иметь скорость, заключенную в единичном интервале скоростей dv вблизи скорости v. Ее называют, поэтому плотностью вероятности.

f(v)=dn/ndv

 

Б-19

1. Кинетическая энергия.

Пусть частица массой движется пол действием силы . Элементарная работа этой силы: ; () . Скалярное произведение ; — проекция вектора приращения скорости на направление вектора . Она равна — приращению модуля вектора скорости, тогда и работа . Отсюда видно, что работа результирующей силы идет на приращение некоторой физической величины , которую называют кинетической энергией и которая является мерой энергии движения материальной точки.

, т.о. (*)

При конечном перемещении из т.1 в т.2

; (**)

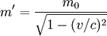
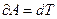Т.е. приращении кинетической энергии частицы при перемещении из т.1 в т.2 равно алгебраической сумме работ всех сил, действующих на частицу на этом перемещении. Если то — кинетическая энергия растет. Если — уменьшается (силы трения). Уравнения (*, **) справедливы в инерциальных и неинерциальных системах отсчета. А в последних, необходимо в работу всех сил учитывать работ сил инерции.