
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа при расширении или сжатии газаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Найдем работу, которая совершается при расширении или сжатии газа, заключенного в сосуде с подвижным поршнем площадью Если давление постоянное, то работа
Б-8 1. Третий закон Ньютона. наблюдения и опыты свидетельствуют, что механическое действие тел одного на другое всегда является взаимодействием. Если тело 2 действует на тело 1, то тело 1 обязательно действует на тело 2. на ведущие колеса автомобиля со стороны шоссе действует сила трения покоя в сторону движения автомобиля, а колеса действуют на шоссе с силами трения покоя в противоположные стороны.
Действию всегда есть равное и противоположное противодействие, взаимодействия двух тел друг на друга равны между собой и направлены в противоположные стороны.
для точек: две материальные точки действуют друг на друга с силами равными по величине, направленные в противоположные стороны вдоль линий их соединения. 2. Гармонические колебания. Уравнение гармонических колебаний. Потенциальная и кинетическая энергия колебаний. Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая частота колебаний, 3. Изопроцессы идеального газа: изохорный. Изохорный процесс, На диаграмме
При изохорном конечном нагреве газа от температуры Т1 до температуры Т2 изменение внутренней энергии равно
Для идеального газа внутренняя энергия это энергия теплового движения молекул, непосредственно не зависящая от объема (расстояния между молекулами), как в реальных газах. При расширении и сжатии газа его Значит, для любого равновесного процесса изменения состояния идеального газа уравнение первого закона термодинамики имеет вид:
Б-9 1. Затухающие колебания. Период колебаний. Добротность. Добротность — характеристика колебательной системы, определяющая остроту резонанса и показывающая, во сколько раз запасы энергии в реактивных элементах контура больше, чем потери энергии на активных за один период колебаний. Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии в течение каждого периода. Колебания в системе с высокой добротностью затухают медленно Общая формула для добротности любой колебательной системы:
где: f — частота колебаний W — энергия, запасённая в колебательной системе Pd — рассеиваемая мощность. 2. Принцип относительности Галилея. Значит ускорение какого-либо тела во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно одинаково. Тогда если одна из систем инерциальная, то другая также будет инерциальная А значит и силы действующие на тела в разных инерциальных системах одинаковы. Масса в Ньютоновской механике также одинакова во всех системах отсчета. Из сказанного следует вывод, что уравнение динамики (Галилей установил, что если взять различные тела, движущиеся равномерно и прямолинейно и связать с каждым из них систему отсчета (такие системы называются инерциальными), то никакими механическими опытами внутри каждой из систем нельзя установить движется эта система или покоится. Мяч в вагоне поезда, который движется прямолинейно с постоянной скоростью, получит такое же ускорение, как и мяч на земле при действии на него такой же силы. Все подобные опыты и наблюдения показывают, что относительно всех инерциальных систем отсчета тела получают одинаковое ускорение при одинаковых воздействиях на них других тел: значит все инерциальные системы равномерны относительно причин ускорений, т.е. силы одинаковы. Во всех инерциальных системах свойства пространства и времени одинаковы, одинаковы также все законы механики. Это утверждение называется принципом относительности Галилея, одного из важнейших принципов ньютоновской механики, (т.е. при 3. Изопроцессы идеального газа: изобарный. Изобарный процесс, Он реализуется при нагревании газа в цилиндре с подвижным поршнем, на который действует постоянное внешнее давление. На рис. изображены процессы изобарного расширения газа при его нагревании (1-2) и изобарного сжатия при его охлаждении (2-3). Элементарная теплота, сообщенная газу в изобарном процессе:
Элементарная работа, совершенная идеальным газом при этом:
Из последнего уравнения можно выяснить смысл
Подставим в первый закон выражения для
Работа газа при изобарном расширении при переходе из состояния 1 в состояние 2, рис.
Если
Б-10 1. Преобразования Галилея. Преобразование Галилея
Подразумевается, что длины отрезков и ход времени не зависит от состояния движения и одинаковы в системе и
После второго дифференцирования
2. Вынужденные колебания. Вынужденные колебания — колебания, происходящие под действием внешней силы, меняющейся во времени. Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 2005; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.014 с.) |

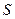 . Внешняя сила, действующая на поршень
. Внешняя сила, действующая на поршень 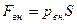 . При перемещении поршня вверх на малое расстояние
. При перемещении поршня вверх на малое расстояние 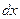 газ совершает элементарную работу
газ совершает элементарную работу 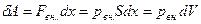 , где
, где  - изменение объема газа. Если изменение объема происходит квазистатически, то в любой момент времени газ находится в равновесном состоянии с внешней средой и его давление
- изменение объема газа. Если изменение объема происходит квазистатически, то в любой момент времени газ находится в равновесном состоянии с внешней средой и его давление 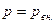 Элементарная работа газа в равновесном (квазистатическом) процессе изменения его объема:
Элементарная работа газа в равновесном (квазистатическом) процессе изменения его объема: 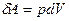 . Т.к.,
. Т.к., 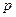 > 0, то при расширении газ совершает положительную работу. При сжатии
> 0, то при расширении газ совершает положительную работу. При сжатии  < 0 – работа газа отрицательна, положительную работу в этом случае совершают внешние силы.
< 0 – работа газа отрицательна, положительную работу в этом случае совершают внешние силы.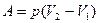 , при
, при 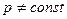 работа вычисляется как сумма элементарных работ, т.е., путем интегрирования:
работа вычисляется как сумма элементарных работ, т.е., путем интегрирования: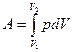 . Это численно равно площади под кривой
. Это численно равно площади под кривой 
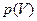 на соответствующем графике, рис. Эти выражения справедливы при любых изменениях объема твердых, жидких и газообразных тел.
на соответствующем графике, рис. Эти выражения справедливы при любых изменениях объема твердых, жидких и газообразных тел.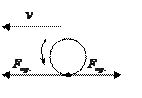 Количественное описание механического взаимодействия было дано Ньютоном в его III-ем законе динамики.
Количественное описание механического взаимодействия было дано Ньютоном в его III-ем законе динамики.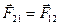
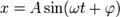 или
или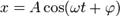 ,
,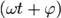 — полная фаза колебаний,
— полная фаза колебаний, 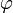 — начальная фаза колебаний
— начальная фаза колебаний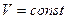 .(закон Шарля).
.(закон Шарля).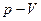 это вертикальная прямая: 1 – 2 нагрев, а 1 - 3 охлаждение. Практически этот процесс проводят, изменяя температуру газа, находящегося в толстостенном сосуде с неизменным объемом. В этом процессе работа не совершается:
это вертикальная прямая: 1 – 2 нагрев, а 1 - 3 охлаждение. Практически этот процесс проводят, изменяя температуру газа, находящегося в толстостенном сосуде с неизменным объемом. В этом процессе работа не совершается: 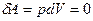 . Вся теплота идет на изменение его внутренней энергии.
. Вся теплота идет на изменение его внутренней энергии. 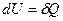 ,
,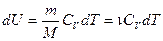 (1), где
(1), где 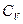 - молярная теплоемкость при постоянном объеме. Из опытов известно, что
- молярная теплоемкость при постоянном объеме. Из опытов известно, что 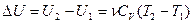 (2), и теплота, сообщенная системе:
(2), и теплота, сообщенная системе: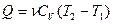 (3)
(3) будет изменяться только за счет изменения кинетической энергии теплового движения, т.е., за счет температуры. Таким образом, соотношения (1) и (2) справедливы для любого процесса изменения состояния идеального газа, а не только изохорного. Внутренняя энергия газа зависит только от его массы, химического состава и температуры. Это подтверждается опытами Гей – Люссака и Джоуля.
будет изменяться только за счет изменения кинетической энергии теплового движения, т.е., за счет температуры. Таким образом, соотношения (1) и (2) справедливы для любого процесса изменения состояния идеального газа, а не только изохорного. Внутренняя энергия газа зависит только от его массы, химического состава и температуры. Это подтверждается опытами Гей – Люссака и Джоуля.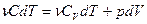 (4)
(4) ,
,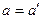 .
.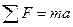 не изменяется при переходе от одной инерциальной системы отсчета к другой или как говорят они инвариантны по отношению к преобразованию координат, соответствующему переходу от одной инерциальной системы отсчета к другой. Это значит что, с механической точки зрения все инерциальные системы отсчета эквивалентны, ни одной из них нельзя отдать предпочтение перед другими. Практически ни какими опытами нельзя установить находится ли данная ИСО в покое или движется равномерно и прямолинейно. Находясь, например, в вагоне поезда, движущегося равномерно и прямолинейно нельзя установить (не выглянув в окно) движется ли он или находится в состоянии покоя. Мяч в вагоне поезда получит такое же ускорение, как и на Земле при действии одинаковой силы. Свободное падение тел и другие механические процессы будут происходить в вагоне также как если бы он покоился. подобное наблюдение и опыты проводил еще Галилей, поэтому положение о том, что все механические явления в разных ИСО протекают одинаковым образом это называется принципом относительности Галилея.
не изменяется при переходе от одной инерциальной системы отсчета к другой или как говорят они инвариантны по отношению к преобразованию координат, соответствующему переходу от одной инерциальной системы отсчета к другой. Это значит что, с механической точки зрения все инерциальные системы отсчета эквивалентны, ни одной из них нельзя отдать предпочтение перед другими. Практически ни какими опытами нельзя установить находится ли данная ИСО в покое или движется равномерно и прямолинейно. Находясь, например, в вагоне поезда, движущегося равномерно и прямолинейно нельзя установить (не выглянув в окно) движется ли он или находится в состоянии покоя. Мяч в вагоне поезда получит такое же ускорение, как и на Земле при действии одинаковой силы. Свободное падение тел и другие механические процессы будут происходить в вагоне также как если бы он покоился. подобное наблюдение и опыты проводил еще Галилей, поэтому положение о том, что все механические явления в разных ИСО протекают одинаковым образом это называется принципом относительности Галилея.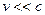 ). Этот принцип выделяет инерциальные системы отсчета, как наиболее важные при изучении механических явлений.)
). Этот принцип выделяет инерциальные системы отсчета, как наиболее важные при изучении механических явлений.)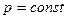 . (Закон Гей -Люссака)
. (Закон Гей -Люссака)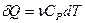 (5), где
(5), где 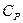 - молярная теплоемкость при постоянном давлении.
- молярная теплоемкость при постоянном давлении.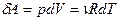 (6), учитывая уравнение Менделеева –Клапейрона.
(6), учитывая уравнение Менделеева –Клапейрона.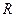 :
: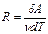 , т.е. универсальная газовая постоянная численно равна работе, совершенной одним молем идеального газа при его изобарном нагревании на 1К.
, т.е. универсальная газовая постоянная численно равна работе, совершенной одним молем идеального газа при его изобарном нагревании на 1К.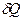 и
и 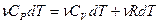 , откуда:
, откуда: 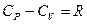 (7) – уравнение Майера для молярных теплоемкостей. Отсюда видно, что при изобарном нагревании газа к нему должна быть подведена большая теплота, чем для такого же изохорного нагревания, разность их равна работе, совершенной газом при изобарном расширении.
(7) – уравнение Майера для молярных теплоемкостей. Отсюда видно, что при изобарном нагревании газа к нему должна быть подведена большая теплота, чем для такого же изохорного нагревания, разность их равна работе, совершенной газом при изобарном расширении.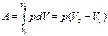 (8).
(8).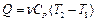 (9), а изменение внутренней энергии в процессе:
(9), а изменение внутренней энергии в процессе: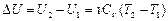 (10).
(10).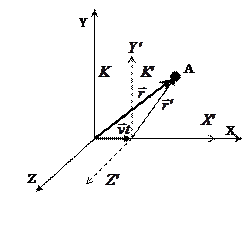 позволяет определить величины при переходе от одной инерциальной системы к другой.
позволяет определить величины при переходе от одной инерциальной системы к другой. 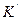 движется со скоростью
движется со скоростью 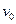 относительно
относительно 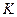 . Взяв начало отсчета времени, момент когда системы совпадали запишем: соотношение между
. Взяв начало отсчета времени, момент когда системы совпадали запишем: соотношение между  и
и 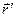 одной и той же точки
одной и той же точки  в
в 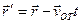 ;
; 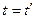 ;
; 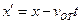 ;
; 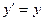 ;
; 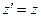 ; (*)
; (*)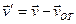 - закон преобразования скоростей.
- закон преобразования скоростей.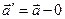
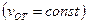 т.е. ускорение не изменяется. Уравнения (*) называются преобразованием Галилея. Итого:
т.е. ускорение не изменяется. Уравнения (*) называются преобразованием Галилея. Итого: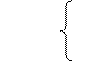
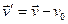 ;
;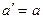 ;
;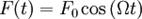 .
.


