
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия вращающегося тела.
Формула справедлива для тела. которое вращается вокруг неподвижной оси. Если тело катится (шар, колесо, и т.д.), то энергия движения складывается из энергии вращения и энергии поступательного движения, т.е. для тела массой
формула справедлива для произвольного движения, поскольку его можно разложить на совокупность вращения относительно оси инерции и поступательного движения. 2. Замедление времени. Под релятивистским замедлением времени обычно подразумевают кинематический эффект специальной теории относительности, заключающийся в том, что в движущемся теле все физические процессы проходят медленнее, чем следовало бы для неподвижного тела по отсчётам времени неподвижной (лабораторной) системе отсчёта. Релятивистское замедление времени проявляется, например, при наблюдении короткоживущих элементарных частиц, образующихся в верхних слоях атмосферы под действием космических лучей и успевающих благодаря ему достичь поверхности Земли. В качестве иллюстрации релятивистского замедления времени часто приводится парадокс близнецов. Количественное описание замедления времени может быть получено из преобразований Лоренца:
где Δt — время, проходящее между двумя событиями движущегося объекта с точки зрения неподвижного наблюдателя, Δt0 — время, проходящее между двумя событиями движущегося объекта с точки зрения наблюдателя связанного с движущемся объектом, v — относительная скорость движения объекта, c — скорость света в вакууме. Точность формулы неоднократно проверена на элементарных частицах и атомах, так что относительная ошибка составляет менее 0,1 ppm. 3. Функция распределения. Распределение Максвелла. Полученная ранее барометрическая формула обязана своим видом тому, что скорости молекул не одинаковы, а распределены определенным образом. Характер этого распределения и определяет вид зависимости плотности молекул от высоты.
n= n0е(-mg/kT)x Пользуясь этой формулой можно найти вид функции распределения молекул по скорости. Возьмем сосуд с газом в пустом пространстве в поле сил тяжести. Газ находится в состоянии равновесия и его молекулы каким-то образом распределены по скорости. Сила тяжести действует на Z компоненту скорости (по вертикали), поэтому найдем распределение молекул по значению составляющей скорости vz. Движение вверх вдоль оси Z сопровождается уменьшением Z компоненты скорости. Если на начальной высоте Z0 скорость равна vz0, то на высоте Z значение vz можно найти из закона сохранения энергии: m(vz0)2/2= m(vz0)2/2+mgZ (*) Молекулы с энергией m(vz0)2/2≤mgZ не могут подняться выше Z=(vz0)2/2g, они после подъема до Z падают вниз c ускорением.
В условиях равновесия число молекул в слое должно быть постоянно, число молекул, проходящих сверху вниз, должно быть равно числу молекул, проходящих снизу вверх. На высоте Z0 число молекул в единице объема с Z компонентой скорости, лежащей в интервале от vz0 до vz0+dvz0 определяется выражением: dnz0= nz0f(vz0)dvz0
∫f(vz0)vzdvz=e-∫f(vz)vzdvz
заменили предел интегрирования т. к. vZ изм. от 0 до µ то есть f(vz)=f(vz0)е(-mg/kT)z (**) Сравнивая это с законом сохранения энергии (*) можно убедится, что функции f(v) должны иметь вид: f(vz)=Ае и f(vz0)=Ae Значит f(vz)=Ае Число молекул в единице объема, с Z компонентой скорости, лежащей в интервале от vZ до vZ+ dvZ выражается формулой dn=nAe dvZ; a dn/n=Ae dvz –
Постоянная А находится из усл. нормировки ∫ dn/n=A∫ e- dvz=1
 Вводится переменная х2 = m(vz)2/2kT => vZ = √2kT/m x => dvz = √ dx Вводится переменная х2 = m(vz)2/2kT => vZ = √2kT/m x => dvz = √ dx
Интеграл сводится к ∫ e-х dx = √ π и тогда A = √m/2πkT И формула распределения принимает вид: f(vz) = dn/ndvZ = (m/2πkT)1/2×e f(vZ)→0 при vZ→∞ Видно,что доля молекул с Z-компонентой скорости равной 0 не равна 0, она равна А и с повышением Т уменьшается. Мы получили распределение молекул по Z- составляющей скорости в поле сил тяжести, но это не означает, что распределение связано с действием силы тяжести. И что mg создает это распределение. Сама барометрическая формула является следствием распределения молекул по скорости. Сила тяжести лишь «проявила» существование в газе распределения, поэтому в f(v) сила тяжести не входит (нет g). Очевидно, что совершенно такие же распределения должны быть и по другим компонентам скорости: dn/ndvx = Ae dn/ndvy = Ae Теперь нужно найти вероятность того, что скорости молекул удовлетворяют трем условиям: vx лежит в пределах от vx до vx+dvx, vy лежит в пределах от vy до vy+dvy, а vz лежит в пределах от vz до vz+dvz. Значения составляющих скоростей молекул по каждой из осей координат не зависят от значений по другим осям. Поэтому, вероятность того, что скорость молекулы одновременно удовлетворяет трем условиям является «вероятностью сложного события», т.е. равна произведению вероятностей. Если обозначить число молекул в единице объема газа dnxyz с составляющими по осям dnx, dny, dnz,то dnxyz/n = A3e dvxdvydvz v2 = Σ(vi)2 Эта формула показывает, сколько молекул из числа находящихся в единице объема обладают скоростями, составляющие которых по осям координат лежат в интервале между vx и vx+dvx, vy и vy+dvy, vz и vz+dvz, т.е. обладают скоростью, лежащей в интервале заданном и по величине и по направлению. В распределении необходимо учесть все любые направления движения. Если собрать все молекулы единицы объема газа со скоростями в интервале от v до v+dv по всем любым направлениям и выпустить их, то они, разлетаясь по всем направлениям, через 1 с окажутся равномерно распределенными в шаровом слое радиусом v и толщиной dv. Число молекул в единице объема этого слоя (объем скоростей) такое же, как и в параллелепипеде объемом dvxdvydvz. Число же молекул во всем слое – это и есть число молекул в единице объема газа, независимо от направления, скорости которых лежат в интервале от v до v+dv: dn = n(m/2πkT)3/2edΩ; dΩ = 4πv2dv, отсюда:
Это и есть закон Максвелла распределения молекул по скоростям. dn/n – вероятность того, что у произвольно выбранной молекулы газа скорость окажется лежащей в интервале от v до v+dv, Другими словами, это доля всех молекул ед. объема, скорости кот. лежат в интервале от v до v+ dv. Величина
f(v) = dn/ndv = (4/√ Она определяет долю молекул в единице объема, скорости которых заключены в единичном интервале скоростей вблизи v, включающем данную скорость. f(v) обращается в 0 при v = 0 и v = ∞, т.е., нет неподвижных молекул и нет молекул с бесконечно большой скоростью. Имеется максимум при vн, т.е. наибольшая часть молекул движется со скоростью v ≈ vн, т.е. вероятность того, что молекула имеет скорость vн – наибольшая, поэтому vн называют наиболее вероятной скоростью. Пользуясь кривой распределения молекул по скоростям можно графически найти долю молекул dn/n в единице объема газа, скорости которых лежат в заданном интервале скоростей dv. Графически - это площадь с основанием dv и высотой f(v). Вся площадь под кривой f(v) соответствует общему числу молекул в единице объема. Вид кривой зависит от природы газа и от Т. С повышением Т максимум смещается в сторону больших скоростей, но площадь под кривой остается постоянной, т.к. n = const. При выводе распред. Максвелла по скоростям совершенно не принимали во внимание столкновения молекул между собой, хотя они изменяют скорость и влияют на распределение. В действительности именно благодаря столкновениям и устанавливается максвелловское распределение по скоростям. При каждом столкновении скорость одной молекулы увеличивается, другой уменьшается. Максвелл предположил, что равновесному состоянию отвечает такое, при котором число молекул, скорости которых увеличиваются при столкновении равно числу молекул, скорости которых уменьшаются при столкновениях. Такому состоянию и соответствует распределение Максвелла. Позже Больцман показал, что если газ находится в состоянии с немаксвелловским распределением, то благодаря столкновениям он сам собой переходит в состояние с максвелловским распределением. Распределение Максвелла (иногда говорят Максвелла -Больцмана) – это равновесное распределение. Теперь можно дать определение хаотичному движению: движение молекул полностью хаотично, если скорости распределены по закону Максвелла.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.30.232 (0.024 с.) |
 Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси, проходящей через него. Разобьем его на частицы с малыми объемами и массами
Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси, проходящей через него. Разобьем его на частицы с малыми объемами и массами  ,
,  …. находящиеся на расстояние
…. находящиеся на расстояние 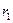 ,
,  … от оси вращения. Разным
… от оси вращения. Разным  будут соответствовать, разные
будут соответствовать, разные 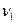 ,
,  … кинетическая энергия вращения всего тела сложится из энергий составляющих его частицу
… кинетическая энергия вращения всего тела сложится из энергий составляющих его частицу т.к.
т.к.  всех частиц одинакова, то
всех частиц одинакова, то  ,
,  … тогда
… тогда т.е.
т.е. 
 , моментом инерции
, моментом инерции  , скоростью поступательного движения
, скоростью поступательного движения  и вращения
и вращения  ;
;  ;
;
 Выделим на высоте Z слой dZ с площадью S=1м2. Газ в слое состоит из движущихся вверх и вниз молекул (нас интересуют молекулы вдоль оси Z). Разница между молекулами снизу и сверху состоит в том, что молекулы, приходящие снизу, имеют Z-компоненту скорости с v≥√2gZ, в то время, как молекулы, приходящие сверху, могут иметь Z-компоненту с любыми скоростями от 0 до ∞.
Выделим на высоте Z слой dZ с площадью S=1м2. Газ в слое состоит из движущихся вверх и вниз молекул (нас интересуют молекулы вдоль оси Z). Разница между молекулами снизу и сверху состоит в том, что молекулы, приходящие снизу, имеют Z-компоненту скорости с v≥√2gZ, в то время, как молекулы, приходящие сверху, могут иметь Z-компоненту с любыми скоростями от 0 до ∞.
 N↑=∫nz0vz0f(vz0)dvz0= nz0∫vz0f(vz0)dvz0
N↑=∫nz0vz0f(vz0)dvz0= nz0∫vz0f(vz0)dvz0 Получим: ∫f(vz0)vz0dvz0= е(-mg/kT)z ∫ f(vz)vzdvz
Получим: ∫f(vz0)vz0dvz0= е(-mg/kT)z ∫ f(vz)vzdvz

 dn/n =(4/√π)(m/2kT) 3/2 v2
dn/n =(4/√π)(m/2kT) 3/2 v2  dv
dv π)(m/2kT) 3/2 v2 edv – функция распределения молекул по скоростям.
π)(m/2kT) 3/2 v2 edv – функция распределения молекул по скоростям.


