
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Молекулярная физика. ТермодинамикаСодержание книги
Поиск на нашем сайте
Основные формулы Количество вещества* тела (системы)
где N – число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему); N A постоянная Авогадро (N A = 6,02×1023 моль–1). Молярная масса вещества
где m – масса однородного тела (системы); n – количество вещества этого тела. Относительная молекулярная масса вещества
где ni – число атомов i -гo химического элемента, входящих в состав молекулы данного вещества; Аr,i – относительная атомная масса этого элемента. Относительные атомные массы приводятся в таблице Д. И. Менделеева. См. также табл. 14 Приложения. Связь молярной массы М с относительной молекулярной массой вещества
где k = 10–3 кг/моль. Количество вещества смеси газов
или
где n i, N i, m i, Mi – соответственно количество вещества, число молекул, масса, молярная масса i -го компонента смеси. Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа)
где т – масса газа, М – молярная масса газа, R – молярная газовая постоянная, n – количество вещества, Т – термодинамическая температура. Опытные газовые законы, являющиеся частными случаями уравнения Менделеева – Клапейрона для изопроцессов: а) закон Бойля – Мариотта (изотермический процесс: T = const, m = const)
или для двух состояний газа
б) закон Гей-Люссака (изобарный процесс: p = const, m = const)
или для двух состояний
в) закон Шарля (изохорный процесс: V = const, m = const)
или для двух состояний
г) объединенный газовый закон (m = const)
где p 1, V 1, T 1 – давление, объем и температура газа в начальном состоянии; p 2, V 2, T 2 – те же величины в конечном состоянии. Закон Дальтона, определяющий давление смеси газов,
где pi – парциальные давления компонентов смеси; n – число компонентов смеси. Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью. Молярная масса смеси газов
где тi, – масса i -гo компонента смеси; Массовая доля i -гo компонента смеси газа (в долях единицы или процентах)
где т – масса смеси. Концентрация молекул
где N – число молекул, содержащихся в данной системе; r – плотность вещества; V – объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.
Основное уравнение кинетической теории газов
где áeПñ – средняя кинетическая энергия поступательного движения молекулы. Средняя кинетическая энергия поступательного движения молекулы
где k – постоянная Больцмана. Средняя полная кинетическая энергия молекулы
где i – число степеней свободы молекулы. Зависимость давления газа от концентрации молекул и температуры
Скорости молекул:
где т 1 – масса одной молекулы. Относительная скорость молекулы
где u – скорость данной молекулы. Удельные теплоемкости газа при постоянном объеме (сV) и постоянном давлении (ср)
Связь между удельной с и молярной С теплоемкостями
Уравнение Майера
Внутренняя энергия идеального газа
Первое начало термодинамики
где Q – теплота, сообщенная системе (газу); D U – изменение внутренней энергии системы; А – работа, совершенная системой против внешних сил. Работа расширения газа:
при адиабатном процессе, где Уравнения Пуассона, связывающие параметры идеального газа при адиабатном процессе:
Термический КПД цикла
где Q 1 – теплота, полученная рабочим телом от теплоотдатчика; Q 2 – теплота, переданная рабочим телом теплоприемнику. Термический КПД цикла Карно
где T 1 и T 2 – термодинамические температуры теплоотдатчика и теплоприемника. Коэффициент поверхностного натяжения
где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости; D E – изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади D S поверхности этой пленки. Формула Лапласа, выражающая давление р, создаваемое сферической поверхностью жидкости:
где R – радиус сферической поверхности. Высота подъема жидкости в капиллярной трубке
где q – краевой угол (q = 0 при полном смачивании стенок трубки жидкостью; q = p при полном несмачивании); R – радиус канала трубки; r – плотность жидкости; g – ускорение свободного падения.
Высота подъема жидкости между двумя близкими и параллельными друг другу плоскостями
Примеры решения задач Пример 1. Определить для серной кислоты: 1) относительную молекулярную массу Мr; 2) молярную массу M. Решение. 1. Относительная молекулярная масса вещества равна сумме относительных атомных масс всех элементов, атомы которых входят в состав молекулы данного вещества, и определяется по формуле
где ni, – число атомов i -го элемента, входящих в молекулу; Ar,i – относительная атомная масса i -го элемента. Химическая формула серной кислоты имеет вид H2SO4. Так как в состав молекулы серной кислоты входят атомы трех элементов, то стоящая в правой части равенства (1) сумма будет состоять из трех слагаемых и эта формула примет вид
Из формулы серной кислоты далее следует, что п 1 = 2 (два атома водорода), n 2 = 1 (один атом серы) и n 3 = 4 (четыре атома кислорода). Значения относительных атомных масс водорода, серы и кислорода найдем в таблице Д. И. Менделеева или в табл. 14 Приложения:
Подставив значения ni, и Аr,i в формулу (2), найдем относительную молекулярную массу серной кислоты:
2. Зная относительную молекулярную массу Мr, найдем молярную массу серной кислоты по формуле
где k =10–3 кг/моль. Подставив в (3) значения величин, получим
Пример 2. Определить молярную массу М смеси кислорода массой m 1 = 25 г и азота массой m 2 = 75 г. Решение. Молярная масса смеси М есть отношение массы смеси m к количеству вещества смеси n:
Масса смеси равна сумме масс компонентов смеси:
Количество вещества смеси равно сумме количеств вещества компонентов:
Подставив в формулу (1) выражения m и n, получим
Применив метод, использованный в примере 1, найдем молярные массы кислорода М 1 и азота М 2:
Подставим значения величин в (2) и произведем вычисления:
Пример 3. Определить число N молекул, содержащихся в объеме V = 1 мм3 воды, и массу т 1 молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекул. Решение. Число N молекул, содержащихся в некоторой системе массой m, равно произведению постоянной Авогадро N A на количество вещества n:
Так как n = т/M, где М – молярная масса, то
Произведем вычисления, учитывая, что M = 18×10–3 кг/моль (см. табл. 14 Приложения):
Массу m 1 одной молекулы можно найти по формуле
Подставив в (1) значения М и N A, найдем массу молекулы воды:
Если молекулы воды плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая ячейка) V 1 = d 3, где d – диаметр молекулы. Отсюда
Объем V 1 найдем, разделив молярный объем V m на число молекул в моле, т. е. на NA:
Подставим выражение (3) в (2):
где Vm = M/ r. Тогда
Проверим, дает ли правая часть выражения (4) единицу длины:
Произведем вычисления:
Пример 4. В баллоне объемом 10 л находится гелий под давлением р 1 = 1 МПа и при температуре Т 1 = 300 К. После того как из баллона было взято m 1 = 10 г гелия, температура в баллоне понизилась до T 2 = 290 К. Определить давление р 2 гелия, оставшегося в баллоне. Решение. Для решения задачи воспользуемся уравнением Менделеева–Клапейрона, применив его к конечному состоянию газа:
где m 2 – масса гелия в баллоне в конечном состоянии; М – молярная масса гелия; R – молярная газовая постоянная.
Из уравнения (1) выразим искомое давление:
Массу m 2 гелия выразим через массу т 1, соответствующую начальному состоянию, и массу m гелия, взятого из баллона:
Массу т 1 гелия найдем также из уравнения Менделеева–Клапейрона, применив его к начальному состоянию:
Подставив выражение массы т 1 в (3), а затем выражение m 2 в (2), найдем
или
Проверим, дает ли формула (5) единицу давления. Для этого в ее правую часть вместо символов величин подставим их единицы. В правой части формулы два слагаемых. Очевидно, что первое из них дает единицу давления, так как состоит из двух множителей, первый из которых (T 2/ T 1) – безразмерный, а второй – давление. Проверим второе слагаемое:
Паскаль является единицей давления. Произведем вычисления по формуле (5), учитывая, что М = 4×10–3 кг/моль (см. табл. 14 Приложения):
Пример 5. Баллон содержит т 1 = 80 г кислорода и m 2 = 320 г аргона. Давление смеси р = 1 МПа, температура Т = 300 К. Принимая данные газы за идеальные, определить объем V баллона. Решение. По закону Дальтона, давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. По уравнению Менделеева–Клапейрона, парциальные давления р 1 кислорода и р 2 аргона выражаются формулами
Следовательно, по закону Дальтона, давление смеси газов
откуда объем баллона
Произведем вычисления, учитывая, что M 1 = 32×10–3 кг/моль, M 2 = 40×10–3 кг/моль (см. табл. 14 Приложения):
Пример 6. Найти среднюю кинетическую энергию áeврñ вращательного движения одной молекулы кислорода при температуре T = 350 К, а также кинетическую энергию E к вращательного движения всех молекул кислорода массой m = 4 г. Решение. На каждую степень свободы молекулы газа приходится одинаковая средняя энергия
Кинетическая энергия вращательного движения всех молекул газа
Число всех молекул газа
где N A – постоянная Авогадро; n – количество вещества. Если учесть, что количество вещества n = m / M, где m – масса газа; М – молярная масса газа, то формула (3) примет вид
Подставив выражение N в формулу (2), получаем
Произведем вычисления, учитывая, что для кислорода М = 32×10–3 кг/моль (см. табл. 14 Приложения):
Пример 7. Вычислить удельные теплоемкости при постоянном объеме cV и при постоянном давлении ср неона и водорода, принимая эти газы за идеальные.
Решение. Удельные теплоемкости идеальных газов выражаются формулами
где i – число степеней свободы молекулы газа; М – молярная масса. Для неона (одноатомный газ) i = 3 и M = 20×10–3 кг/моль (см. табл. 14 Приложения). Произведем вычисления:
Для водорода (двухатомный газ) i = 5 и М = 2×10–3кг/моль. Тогда
Пример 8. Вычислить удельные теплоемкости cV и c р смеси неона и водорода, если массовые доли неона и водорода составляют w 1 = 80% и w 2 = 20%. Значения удельных теплоемкостей газов взять из предыдущего примера. Решение. Удельную теплоемкость сV смеси при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания смеси на D T, выразим двумя способами:
где cV ,1 – удельная теплоемкость неона; cV ,2 – удельная теплоемкость водорода. Приравняв правые части (1) и (2) и разделив обе части полученного равенства на D T, получим
или
где Рассуждая так же, получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:
Произведем вычисления:
Пример 9. Кислород массой m = 2 кг занимает объем V 1 = 1 м3 и находится под давлением р 1 = 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V 2 = 3 м, а затем при постоянном объеме до давления р 3 = 0,5 МПа. Найти изменение D U внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса. Решение. Изменение внутренней энергии газа
где i – число степеней свободы молекул газа (для двухатомных молекул кислорода i = 5); D T = T 3 – T 1 – разность температур газа в конечном (третьем) и начальном состояниях. Начальную и конечную температуру газа найдем из уравнения Менделеева–Клапейрона
Работа расширения газа при постоянном давлении выражается формулой
Работа газа, нагреваемого при постоянном объеме, равна нулю:
Следовательно, полная работа, совершаемая газом,
Согласно первому началу термодинамики, теплота Q, переданная газу, равна сумме изменения внутренней энергии D U и работы А:
Произведем вычисления, учтя, что для кислорода M = 32×10–3 кг/моль (см. табл. 14 Приложения):
График процесса приведен на рис. 7.
Решение. Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением
где g – отношение теплоемкостей газа при постоянном давлении и постоянном объеме; n 1 = V 2/ V 1. Отсюда получаем следующее выражение для конечной температуры:
Работа А 1 газа при адиабатном расширении может быть определена по формуле
где СV – молярная теплоемкость газа при постоянном объеме. Работа A 2 газа при изотермическом процессе может быть выражена в виде
где n 2 = V 2/ V 3. Произведем вычисления, учитывая, что для водорода как двухатомного газа g = 1,4, i = 5 и М = 2×10–3 кг/моль:
Так как 50,4 = 1,91 (находится логарифмированием), то
Знак минус показывает, что при сжатии работа газа совершается над газом внешними силами. График процесса приведен на рис. 8. Пример 11. Тепловая машина работает по обратимому циклу Карно. Температура теплоотдатчика 7J = = 500 К. Определить термический КПД h цикла и температуру T 2 теплоприемника тепловой машины, если за счет каждого килоджоуля теплоты, полученной от теплоотдатчика, машина совершает работу А = 350 Дж. Решение. Термический КПД тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу. Термический КПД выражается формулой
где Q 1 – теплота, полученная от теплоотдатчика; А – работа, совершенная рабочим телом тепловой машины. Зная КПД цикла, можно по формуле
Произведем вычисления:
Пример 12. Найти добавочное давление внутри мыльного пузыря диаметром d =10 см. Какую работу нужно совершить, чтобы выдуть этот пузырь? Решение. Пленка мыльного пузыря имеет две сферические поверхности: внешнюю и внутреннюю. Обе поверхности оказывают давление на воздух, заключенный внутри пузыря. Так как толщина пленки чрезвычайно мала, то диаметры обеих поверхностей практически одинаковы. Поэтому добавочное давление
где r – радиус пузыря. Так как r = d/2, то
Работа, которую нужно совершить, чтобы, растягивая пленку, увеличить ее поверхность на D S, выражается формулой
В данном случае S – общая площадь двух сферических поверхностей пленки мыльного пузыря; S 0 – общая площадь двух поверхностей плоской пленки, затягивавшей отверстие трубки до выдувания пузыря. Пренебрегая S 0, получаем
Произведем вычисления:
Задачи для самостоятельного решения 1. Вычислить массу т атома азота. [2,33×10–26 кг] 2. Плотность газа с при давлении с = 96 кПа и температуре t = 0°C равна 1,35 г/л. Найти молярную массу М газа. [32×10–3 кг/моль] 3. Определить давления р 1 и p 2 газа, содержащего N = 109 молекул и имеющего объем V = 1 см3, при температурах T 1 = 3К и T 2 = 1000К. [41,4 нПа; 13,8 мкПа] 4. При температуре t = 35°С и давлении p = 708 кПа плотность некоторого газа р = 12,2 кг/м3. Определить относительную молекулярную массу Mr, газа. [44,1] 5. Какой объем V занимает смесь азота массой m1 = 1 кг и гелия массой т 2 = 1 кг при нормальных условиях? [6,4 м3] 6. В баллоне вместимостью V =15 л находится смесь, содержащая m 1 = 10 г водорода, m 2 = 54 г водяного пара и m 3 = 60 г оксида углерода. Температура смеси t = 27°. Определить давление. [1,69 МПа] 7. Найти полную кинетическую энергию, а также кинетическую энергию вращательного движения одной молекулы аммиака NH3 при температуре t = 27°С. [1,24×10–20 Дж; 6,2×10–21 Дж] 8. Определить удельные теплоемкости cV и ср газообразного оксида углерода СО. [743 Дж/(кг×К); 1,04 кДж/(кг×К)] 9. Смесь газа состоит из кислорода О2 с массовой долей w = 85% и озона О3 с массовой долей w 2=15%. Определить удельные теплоемкости сV и ср этой газовой смеси. [629 Дж/(кг×К); 877 Дж/(кг×К)] 10. Газовая смесь состоит из азота массой m1 = 3 кг и водяного пара массой т 2 = 1 кг. Принимая эти газы за идеальные, определить удельные теплоемкости сV и ср газовой смеси. [902 Дж/(кг×К); 1,24 кДж/(кг×К)] 11. Молекула газа состоит из двух атомов; разность удельных теплоемкостей газа при постоянном давлении и постоянном объеме равна 260 Дж/(кг×К). Найти молярную массу газа и его удельные теплоемкости сV и ср. [32×10–3 кг/моль; 650 Дж/(кг×К); 910 Дж/(кг×К)]
13. Один киломоль двухатомного идеального газа совершает замкнутый цикл, график которого изображен на рис. 9. Определить: 1) теплоту Q 1, полученную от теплоотдатчика; 2) теплоту Q 2, переданную теплоприемнику; 3) работу А, совершаемую газом за один цикл; 4) термический КПД h цикла. [7,61 МДж; 7,19 МДж; 0,4 МДж; 5,3%] 14. Водород занимает объем V = 10 м3 при давлении p 1 = 0,l МПа. Его нагрели при постоянном объеме до давления р 2 = 0,3 МПа. Определить изменение D Q внутренней энергии газа, работу А, совершенную им, и теплоту Q, сообщенную газу. [5 МДж; 0; 5 МДж] 15. Кислород при неизменном давлении р = 80 кПа нагревается. Его объем увеличивается от V 1 = 1 м3 до V 2 = 3 м3. Определить изменение D U внутренней энергии кислорода, работу А, совершенную им при расширении, а также теплоту Q, сообщенную газу. [400 кДж; 160 кДж; 560 кДж] 16. В цилиндре под поршнем находится азот, имеющий массу m = 0,6 кг и занимающий объем V 1 = l,2 м3, при температуре T 1 = 560 К. В результате нагревания газ расширился и занял объем V 2 = 4,2 м3, причем температура осталась неизменной. Найти изменение D U внутренней энергии газа, совершенную им работу А и теплоту Q, сообщенную газу. [0; 126 кДж; 126 кДж] 17. В бензиновом автомобильном двигателе степень сжатия горючей смеси равна 6,2. Смесь засасывается в цилиндр при температуре t 1 = 15°С. Найти температуру t 2 горючей смеси в конце такта сжатия. Горючую смесь рассматривать как двухатомный идеальный газ; процесс считать адиабатным. [324°С] 18. Газ совершает цикл Карно. Температура теплоотдатчика в три раза выше температуры теплоприемника. Теплоотдатчик передал газу Q 1 = 41,9 кДж теплоты. Какую работу совершил газ? [28,1 кДж] 19. Какую энергию надо затратить, чтобы выдуть мыльный пузырь диаметром d = 12 cм? Каково будет добавочное давление внутри этого пузыря? [3,62 мДж; 2,66 Па] 20. На нижнем конце трубки диаметром d = 0,2см повисла шарообразная капля воды. Найти диаметр этой капли. [4,42 мм] 21. В сосуд с ртутью частично погружены две вертикально расположенные и параллельные друг другу стеклянные пластинки. Расстояние между пластинками d = 1 мм. Определить разность D h уровней ртути в сосуде и между пластинками, краевой угол принять равным 138°. [–5,57 мм] Контрольная работа 2 Таблица вариантов для специальностей, учебными планами которых предусмотрено по курсу физики шесть контрольных работ
201. Определить количество вещества n и число N молекул кислорода массой m = 0,5 кг. 202. Сколько атомов содержится в ртути: 1) количеством вещества n = 0,2 моль; 2) массой m = 1 г? 203. Вода при температуре t = 4°С занимает объем V = 1 см3. Определить количество вещества n и число N молекул воды. 204. Найти молярную массу М и массу m м одной молекулы поваренной соли. 205. Определить массу m м одной молекулы углекислого газа. 206. Определить концентрацию n молекул кислорода, находящегося в сосуде вместимостью V = 2 л. Количество вещества n кислорода равно 0,2 моль. 207. Определить количество вещества n водорода, заполняющего сосуд объемом V = 3 л, если концентрация молекул газа в сосуде n = 2·1018 м–3. 208. В баллоне вместимостью V = 3л содержится кислород массой m = 10 г. Определить концентрацию n молекул газа. 209. Определить относительную молекулярную массу Мr: 1) воды; 2) углекислого газа; 3) поваренной соли. 210. Определить количество вещества n и число N молекул азота массой т = 0,2 кг. 211. В цилиндр длиной l = 1,6 м, заполненный воздухом при нормальном атмосферном давлении р 0, начали медленно вдвигать поршень площадью основания S = 200 см2. Определить силу F, действующую на поршень, если его остановить на расстоянии l 1 =10 см от дна цилиндра. 212. В баллоне находится газ при температуре Т 1 = 400 К. До какой температуры T 2 надо нагреть газ, чтобы его давление увеличилось в 1,5 раза? 213. Баллон вместимостью V =20 л заполнен азотом при температуре T = 400 К. Когда часть газа израсходовали, давление в баллоне понизилось на D р = 200кПа. Определить массу m израсходованного газа. Процесс считать изотермическим. 214. В баллоне вместимостью V = 15 л находится аргон под давлением р 1 = 600 кПа и при температуре T 1 = 300 К. Когда из баллона было взято некоторое количество газа, давление в баллоне понизилось до р 2 = 400кПа, а температура установилась T 2 = 260 К. Определить массу m аргона, взятого из баллона. 215. Два сосуда одинакового объема содержат кислород. В одном сосуде давление p 1 = 2 МПа и температура T 1 = 800К, в другом р 2 = 2,5 МПа, T 2 = 200 К. Сосуды соединили трубкой и охладили находящийся в них кислород до температуры T = 200 К. Определить установившееся в сосудах давление р. 216. Вычислить плотность r азота, находящегося в баллоне под давлением р = 2 МПа и имеющего температуру Т = 400 К. 217. Определить относительную молекулярную массу Мr газа, если при температуре Т = 154 К и давлении p = 2,8 МПа он имеет плотность r = 6,1 кг/м3. 218. Найти плотность r азота при температуре Т = 400 К и давлении р = 2 МПа. 219. В сосуде вместимостью V = 40 л находится кислород при температуре T =300 К. Когда часть газа израсходовали, давление в баллоне понизилось на D p = 100 кПа. Определить массу т израсходованного кислорода. Процесс считать изотермическим. 220. Определить плотность с водяного пара, находящегося под давлением р = 2,5 кПа и имеющего температуру T =250 К. 221. Определить внутреннюю энергию U водорода, а также среднюю кинетическую энергию áeñ молекулы этого газа при температуре T = 300 К, если количество вещества n этого газа равно 0,5 моль. 222. Определить суммарную кинетическую энергию E K поступательного движения всех молекул газа, находящегося в сосуде вместимостью V = 3 л под давлением p = 540 кПа. 223. Количество вещества гелия n = 1,5 моль, температура Т = 120 К. Определить суммарную кинетическую энергию E K поступательного движения всех молекул этого газа. 224. Молярная внутренняя энергия U m некоторого двухатомного газа равна 6,02 кДж/моль. Определить среднюю кинетическую энергию áeврñ вращательного движения одной молекулы этого газа. Газ считать идеальным. 225. Определить среднюю кинетическую энергию áeñ одной молекулы водяного пара при температуре Т = 500 К. 226. Определить среднюю квадратичную скорость áuквñ молекулы газа, заключенного в сосуд вместимостью V = 2 л под давлением p = 200 кПа. Масса газа m = 0,3 г. 227. Водород находится при температуре T = 300 К. Найти среднюю кинетическую энерги
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.77 (0.013 с.) |

 ,
,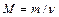
 ,
,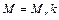 ,
, ,
, ,
,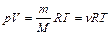 ,
,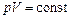 ,
, ;
; ,
, ;
;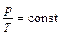 ,
, ;
; , или
, или  ,
, ,
, ,
,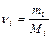 – количество вещества i -го компонента смеси; n – число компонентов смеси.
– количество вещества i -го компонента смеси; n – число компонентов смеси.
 ,
,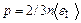 ,
, ,
, ,
,
 – средняя квадратичная;
– средняя квадратичная; – средняя арифметическая;
– средняя арифметическая; – наиболее вероятная,
– наиболее вероятная,
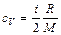 ,
,  .
. ,
,  .
.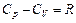
 .
.
 в общем случае;
в общем случае; при изобарном процессе;
при изобарном процессе;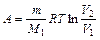 при изотермическом процессе;
при изотермическом процессе; , или
, или 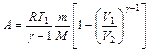
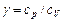 – показатель адиабаты.
– показатель адиабаты. ,
, 
 .
. ,
,  .
.

 , или
, или  ,
,
 ,
,
 . (2)
. (2) ,
,  ,
, 

 .
.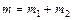 .
.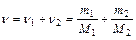 .
.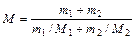 . (2)
. (2) ;
;  .
.

 .
.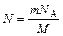 . Выразив в этой формуле массу как произведение плотности на объем V, получим
. Выразив в этой формуле массу как произведение плотности на объем V, получим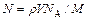 .
. .
. . (1)
. (1)
 . (2)
. (2) . (3)
. (3) ,
,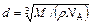 . (4)
. (4) .
.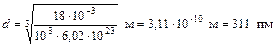 .
. , (1)
, (1) . (2)
. (2) . (3)
. (3) (4)
(4) ,
,
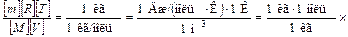



 ,
,  .
.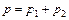 ,
,  ,
, . (1)
. (1)
 , где k – постоянная Больцмана; Т – термодинамическая температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная) соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода
, где k – постоянная Больцмана; Т – термодинамическая температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная) соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода . (1)
. (1) . (2)
. (2) , (3)
, (3)
 . (4)
. (4) ;
; .
. ;
; .
.

 , (1)
, (1) , (2)
, (2) . Отсюда
. Отсюда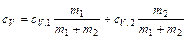 ,
, ,
, и
и 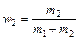 .
.

 ;
;
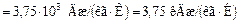 .
.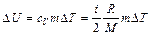 ; (1)
; (1) , откуда
, откуда .
.

 .
. ;
; ;
; ;
; ;
; ;
;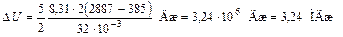 ;
;
 Пример 10. В цилиндре под поршнем находится водород массой т = 0,02 кг при температуре T 1 = 300 К. Водород сначала расширился адиабатно, увеличив свой объем в п 1 = 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в n 2 = 5 раз. Найти температуру в конце адиабатного расширения и работу, совершаемую газом при этих процессах. Изобразить процесс графически.
Пример 10. В цилиндре под поршнем находится водород массой т = 0,02 кг при температуре T 1 = 300 К. Водород сначала расширился адиабатно, увеличив свой объем в п 1 = 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в n 2 = 5 раз. Найти температуру в конце адиабатного расширения и работу, совершаемую газом при этих процессах. Изобразить процесс графически. ,
,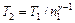 .
. ,
, , или
, или  ,
, .
. ;
; ;
;

 ,
, определить температуру охладителя T 2:
определить температуру охладителя T 2: .
. ;
;  ;
;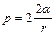 ,
, .
. , или
, или  .
. .
.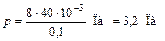 ;
;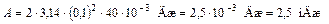
 12. Найти среднюю длину á l ñ свободного пробега молекулы водорода при p = 133 мПа и t = –173°С. [4,4 см).
12. Найти среднюю длину á l ñ свободного пробега молекулы водорода при p = 133 мПа и t = –173°С. [4,4 см).


