
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретический анализ термодинамических процессов в идеальном газеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Целью расчета и исследования любого термодинамического процесса является определение термических параметров рабочего тела в начале и конце процесса, а также определение полученной (затраченной) работы и теплоты, подведенной (отведенной) в процессе. Для этого необходимо знать: – уравнение состояния рабочего тела (молекулярную массу используемого газа, находящегося в идеально-газовом состоянии); – уравнение внутренней энергии (количество атомов, образующих молекулу газа); – уравнение процесса в одной из термических систем координат (p,v; p,T или T,v); – состояние рабочего тела в начале процесса (два независимых параметра, либо величины, из которых их можно определить); – значение одного из изменяющихся параметров в конце процесса (либо величину, из которой его можно рассчитать). Выбор тех или иных исходных данных обусловлен характером процесса либо решаемой задачи. Например, могут быть заданы параметры рабочего тела в одном из его состояний и значения теплоты либо работы процесса, а требуется определить параметры в другом состоянии. Ниже приводятся примеры расчета и анализа термодинамических процессов, используемых в технике. Поскольку чаще всего используется совокупность термодинамических процессов, задачи составлены так, чтобы учащийся с самого начала осваивал методику построения и расчета такой совокупности процессов (цикла). Для облегчения восприятия приводимых ниже расчетов и анализа термодинамических процессов в идеальном газе в табл.1 приведены соотношения между изменяющимися в них термическими параметрами состояния, а в табл. 2 – формулы для расчета теплоты и работы процессов.
Таблица 1 Аналитические соотношения между термическими параметрами состояния идеального газа в термодинамических процессах
Таблица 2 Соотношения для расчета теплоты и работы процессов
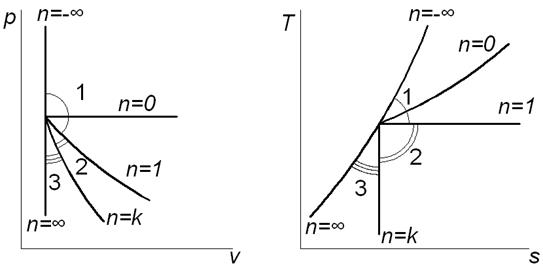
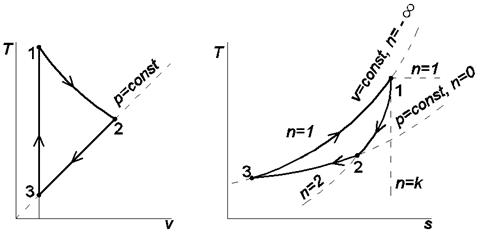
На рис. 1.1 изображена совокупность политропных процессов расширения, исходящих из одной точки. Соотношения между изменением внутренней энергии, теплотой и работой политропных процессов расширения, протекающих в трёх зонах, отмеченных на рисунке, представлены в табл. 3.
Рис. 1.1. Сопоставление политропных процессов расширения В координатах p,v и T,s Таблица 3 Соотношения между изменениями внутренней энергии, теплоты и работы в политропных процессах расширения
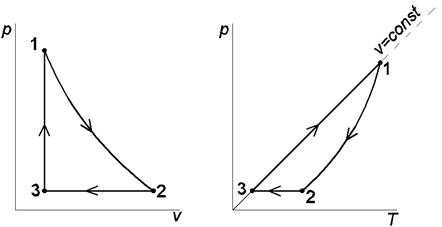
Цикл с политропным расширением, изобарным сжатием и изохорным подводом теплоты Выполним расчёт и анализ указанного цикла на примере решения следующей задачи. Задача. 11м3 криптона политропно расширяется до 1/4 первоначального давления, затем изобарно сжимается до первоначального объема, наконец, изохорно возвращается в исходное состояние. Начальные параметры рабочего тела: давление р 1= 0,2 МПа и температура t 1= 350 °С. Показатель политропы расширения n = 2. Определить параметры рабочего тела в характерных точках указанной совокупности процессов, суммарные значения теплоты и работы заданного количества криптона в цикле, а также изменения удельных: - внутренней энергии в политропном процессе 1-2; - энтропии в изобарном процессе 2-3; - энтальпии в изохорном процессе 3-1 ( рис. 1.2 ). Изобразить указанный цикл в термических и тепловой диаграммах.
Рис.1.2. Изображения заданной совокупности процессов на термических и тепловой диаграммах: 1-2 – политропное расширение; 2-3 – изобарное сжатие; 3-1 – изохорный подвод теплоты Решение Криптон (Kr) – одноатомный газ, поэтому его показатель адиабаты k = 1,6667. По таблице Менделеева определяем молекулярную массу криптона: mKr = 83,8 кг/кмоль. Удельная газовая постоянная криптона
Масса криптона, участвующего в заданной совокупности процессов (цикле), определяем из уравнения Клапейрона для М кг рабочего тела в идеально-газовом состоянии
Рассчитываем термические параметры рабочего тела в характерных точках цикла. Точка 1 - абсолютная температура в Кельвина
Т 1 = t 1°С+273,15 = 350 +273,15 = 623,15К; - удельный объем в начальной точке цикла определяем из уравнения Клапейрона для 1кг идеального газа рv = RT
Точка 2 Процесс 1-2 – политропный, поэтому в нём изменяются все три термических параметра состояния в соответствии с соотношением
Так как по условию задачи р 1/ р 2 = 4, то р 2= р 1/4 = 0,2/4 = 0,05 МПа, тогда
Температуру в точке 2 рассчитываем из приведенного выше соотношения
Для проверки рассчитываем значение Т 2 из уравнения состояния
Точка 3 Процесс 2-3 – изобарный, поэтому р 3= р 2= 0,05 МПа. Соотношение между параметрами в изобарном процессе
По условию задачи v3 = v1 = 0,3091 м3/кг.
Результаты расчетов записываем в таблицу:
Рассчитываем количество удельной теплоты, подводимой (отводимой) в заданных процессах. В политропном процессе 1-2
где cv – изохорная теплоемкость. По упрощенной молекулярно-кинетической теории МКТ cv =(3+ j)· R /2; здесь j – количество различимых вращательных степеней свободы атомов в молекуле. Криптон одноатомный газ, поэтому j = 0
Поскольку рассчитанное значение q 1-2 < 0, в процессе 1-2 теплота отводится от рабочего тела в окружающую среду. В изобарном процессе 2-3
где сp = (5+ j) R /2 = 2,5 R = 2,5·0,0992 = 0,2480 кДж/(кг·К) – изобарная теплоёмкость. Так как q2-3<0, то и в этом процессе теплота отводится.
В изохорном процессе 3-1
Следовательно, в этом процессе теплота подводится. Суммарное количество теплоты, подводимой (отводимой) в цикле: – удельное (для 1кг рабочего тела)
– общее (для Мкг рабочего тела)
Следовательно, теплоты подводится больше, чем отводится. Разность подводимой и отводимой теплоты (549,87 кДж) в рассматриваемом цикле превращается в работу. Определяем значения удельных работ, получаемых (затрачиваемых) в процессах цикла: — в политропном процессе расширения 1-2
— в изобарном процессе сжатия 2-3
— в изохорном процессе нагрева 3-1
Суммарное количество работы, полученной в цикле: – удельное (работа 1 кг газа)
– общее (работа М кг газа)
Результаты расчетов значений теплоты и работы сводим в таблицу
Изменение внутренней энергии в политропном процессе расширения 1-2
Проверка.
Из первого закона термодинамики следует
Из выполненных расчетов следует, что в политропном процессе расширения 1-2 работа совершается за счет внутренней энергии. Кроме того, часть внутренней энергии (15,45 кДж/кг) отводится в окружающую среду в виде теплоты.
Изменение энтропии в изобарном процессе 2-3
Поскольку Δ s 23<0, теплота в этом процессе отводится, что подтверждается приведенными выше расчетами. Изменение энтальпии в изохорном процессе 3-1
Проверка.
Из первого закона термодинамики следует
где техническая работа в изохорном процессе
В изохорном процессе подводимая теплота накапливается в видевнутренней энергии рабочего тела, что проявляется в повышении давления, так как dh = du + vdp.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 916; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.92.22 (0.009 с.) |


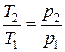 прямо пропорционально
прямо пропорционально
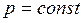
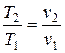 прямо пропорционально
прямо пропорционально
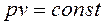
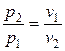 обратно пропорционально
обратно пропорционально
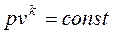 , где k – показатель адиабаты, зависящий от количества атомов в молекуле газа
, где k – показатель адиабаты, зависящий от количества атомов в молекуле газа
 с ростом Т растет р, и уменьшается v.
с ростом Т растет р, и уменьшается v.
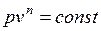 , где n – показатель политропы (может принимать значение от -∞ до +∞)
, где n – показатель политропы (может принимать значение от -∞ до +∞)
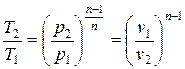 с ростом Т увеличивается р, и уменьшается v.
с ростом Т увеличивается р, и уменьшается v.

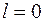
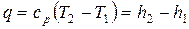
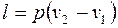
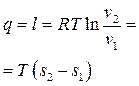
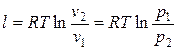
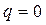
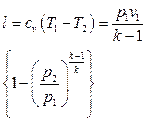
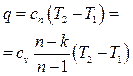
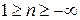
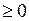
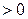
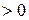
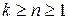
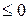


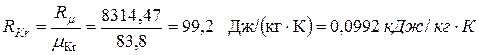 .
.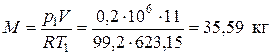 .
. .
.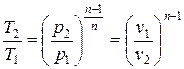 .
.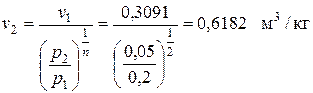 .
.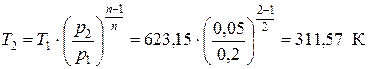 .
.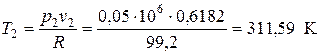 .
. ® тогда
® тогда  .
.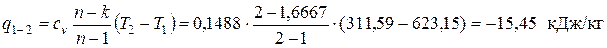 ,
,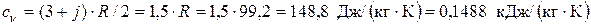 .
. ,
,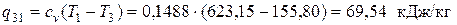 .
.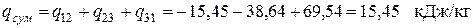 ;
;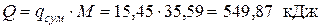 .
.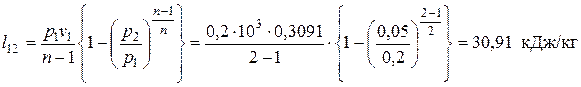 ,
,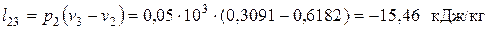 .
.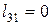 .
.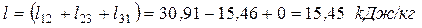 ;
;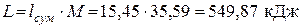 .
.
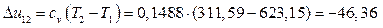 кДж/кг.
кДж/кг.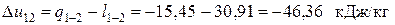 .
.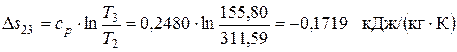 .
.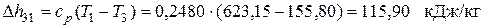 .
.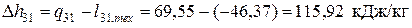 ,
,
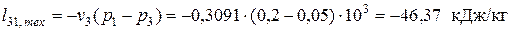 .
.


