
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цикл с изохорным подводом теплоты, изобарным расширеним и политропным сжатиемСодержание книги
Поиск на нашем сайте
Выполним расчёт и анализ указанного цикла на примере решения следующей задачи. Задача. 1 кг воздуха, находящегося при температуре минус 10,3 °С и разрежении 50 мм рт. ст., изохорно нагревается до манометрического давления 1,0 кгс/см2, а затем изобарно расширяется до такого объёма, чтобы политропно возвратиться в начальное состояние. Показатель политропы п = –1,3. Атмосферное давление 100,5 кПа. Определить параметры воздуха в характерных точках цикла, а также степень его термодинамического совершенства. Изобразить цикл, образованный указанными процессами, на термических и тепловой диаграммах. Решение Термические параметры рабочего тела (воздуха) в характерных точках цикала:
Точка 1 - давление
так как 750 мм рт. ст. = 1 бар - температура - удельный объем
где
Точка 2 - давление
так как 1 кг/см2 = 98066,5 Па;
- удельный объем
- температура
Точка 3 - давление (по условию процесс 2-3 изобарный) - удельный объем (процесс 3-1 политропный).
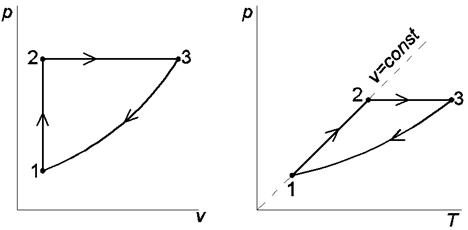
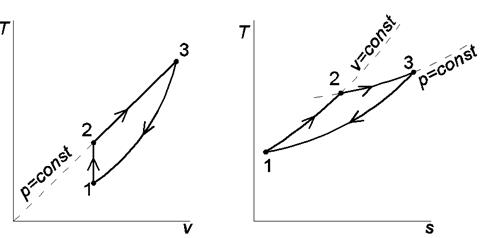
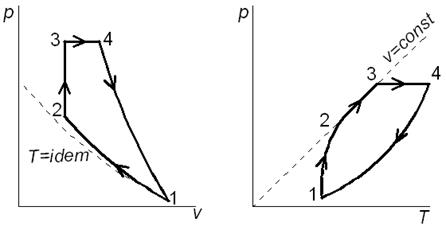
Рис.1.3. Изображения заданного цикла на термических и тепловой диаграммах: 1-2 – изохорный подвод теплоты; 2-3 – изобарное расширение; 3-1 – политропное сжатие - температура
Результаты расчетов записываем в таблицу
Отводимая в цикле теплота
где изохорная теплоёмкость сv по упрощенной МКТ для воздуха, как двухатомного газа, рассчитывается из соотношения
Подводимая в цикле теплота
где изобарная теплоёмкость ср в соответствии с МКТ равна
Термический КПД рассматриваемого цикла
Термический КПД предельного цикла Карно
Степень совершенства рассчитанного цикла
Итак, рассмотренный термодинамический цикл значительно уступает по эффективности соответствующему предельному циклу Карно. Это обусловлено тем, что количества подводимой и отводимой теплоты в цикле близки.
1.4. Цикл с адиабатным сжатием, изохорным подводом теплоты, изобарным и политропным расширением Выполним исследование заданной совокупности процессов на примере решения следующей задачи. Задача 1 нм3 метана адиабатно сжимается до 1/5 первоначального объема, затем изохорно нагревается при подводе 200 кДжтеплоты, затем изобарно расширяется с подводом 100 кДж теплоты, наконец, политропно возвращается в начальное состояние. Изобразить цикл на термических и тепловой диаграммах. Определить параметры газа в характерных точках образовавшегося цикла и его степень совершенства. Начальные параметры рабочего тела р 1= 1 бар, t 1 = 100 °С. Решение Прежде всего, изобразим цикл на диаграммах состояния (рис.1.4). Затем рассчитываем: - удельную газовую постоянную метана (СН4)
- удельный объем метана в точке 1
- параметры метана в точке 2 (процесс 1-2 – адиабатный): удельный объём температура давление где k = 1,33 – показатель адиабаты для газов, молекулы которых содержат три и большее количество атомов.
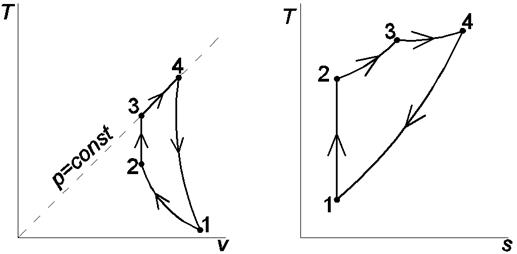
Рис. 1.4. Изображения исследуемого цикла на термических и тепловой диаграммах: 1-2 – адиабатное сжатие; 2-3 – изохорный подвод теплоты; 3-4 – изобарный подвод теплоты; 4-1 – политропный отвод теплоты Для дальнейших расчетов необходимо определить массу одного нм3 метана из уравнения состояния идеального газа
При определении параметров точки 3 используем заданное значение теплоты, подводимой в процессе. Удельная теплота в изохорном процессе 2-3 рассчитывается из соотношения
где qv = Qv / М = 200/0,7139 = 280,15 кДж/кг – удельная теплота, подводимая в изохорном процессе; cv – изохорная теплоёмкость сv, которая по упрощенной МКТ рассчитывается из соотношения
где j – количество вращательных степеней свободы атомов в молекуле (для трёх- и многоатомных газов j = 3). В изохорном процессе температура и давление изменяются прямо пропорционально
Параметры точки 4 ( процесс 3-4 –изобарный)
р4 = р3 = 1,0912 МПа. Удельная теплота в изобарном процессе рассчитывается из соотношения
отсюда где qp = Qp/М = 100/0,7139 = 140,08 кДж/кг – удельная теплота, подводимая в изобарном процессе (см. условие задачи), cp – изобарная теплоёмкость метана, рассчитываемая из соотношения
В изобарном процессе температура и удельный объём изменяются прямо пропорционально
Результаты расчетов записываем в таблицу
Критерием точности выполненных расчётов является равенство суммы работΣ l, рассчитанных через параметры p и v и суммы теплот Σ q, рассчитанных через Т, ср и сv для всех процессов, образующих цикл. Рассчитываем значения деформационной работы во всех термодинамических процессах, образующих исследуемый цикл: – работа в адиабатном процессе сжатия 1-2
– работа в изохорном процессе 2-3 – работа расширения в изобарном процессе 3-4
– работа в политропном процессе расширения 4-1
где п – показатель политропы расширения, рассчитанный из соотношения
Далее рассчитываем значения теплоты в процессах, образующих цикл: – в адиабатном процессе сжатия 1-2 – в изохорном процессе 2-3 ( см. стр.19 ) – в изобарном процессе 3-4 (стр.20) – в политропном процессе 4-1
Результаты расчетов сводим в следующую таблицу:
Из таблицы видно, что сумма работ отличается от суммы теплот на 0,38 кДж/кг, то есть на 0,41 %. Это свидетельствует об удовлетворительной точности расчетов. Термический КПД исследуемого цикла
где q 1 = q 2-3 + q 3-4 = 280,15 + 140,08 = 420,23 кДж/кг – теплота, подводимая в цикле. Термический КПД предельного цикла Карно
Степень совершенства рассматриваемого цикла
Следовательно, эффективность заданного цикла ниже эффективности соответствующего предельного цикла Карно почти на 62 %.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 746; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.009 с.) |

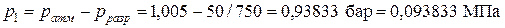 ,
,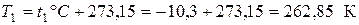
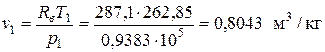 ,
,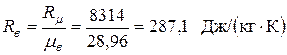 – удельная газовая постоянная воздуха.
– удельная газовая постоянная воздуха.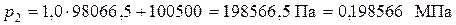 ,
,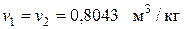 , (по условию задачи процесс 1-2 изохорный);
, (по условию задачи процесс 1-2 изохорный);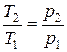 ®
®  .
.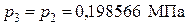 ;
;
 ®
® 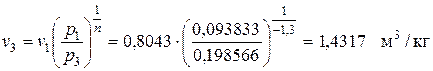 ;
;
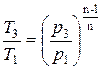
 .
. ,
,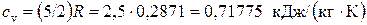 .
.
 .
. .
.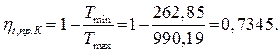

 ;
;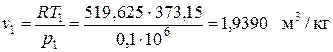 ;
;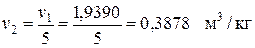 ;
;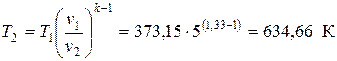 ;
;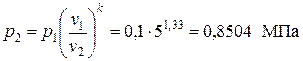 ,
,
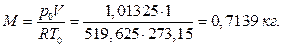
 , тогда
, тогда 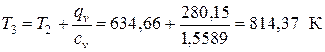 ,
, ,
, , отсюда
, отсюда  .
.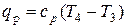 ,
, ,
,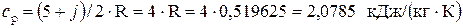 .
. , отсюда
, отсюда 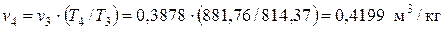 .
.
 ;
;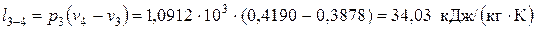 ;
;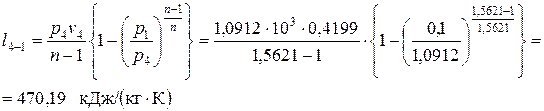 ,
,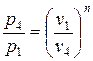 , отсюда
, отсюда 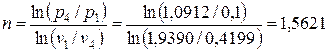 .
. ;
; ;
; ;
;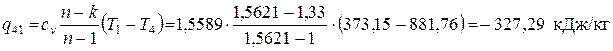 .
.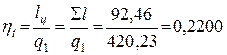 ,
, .
.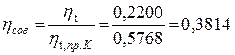 .
.


