Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термодинамический анализ процессов в реальном газеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Цель исследования термодинамических процессов в реальном газе и необходимые исходные данные такие же, как и для идеального газа (см. пара-граф 1.1 настоящего пособия). При этом следует иметь в виду, что для воды и водяного пара, а также для хладагентов имеющиеся таблицы термодинамических свойств и диаграммы состояния заменяют уравнения состояния и уравнения для внутренней энергии, то есть позволяют определять данные, необходимые для расчета термодинамических процессов. При расчете и исследовании процессов в реальном газе используют табличный, графический (с помощью диаграмм) либо аналитический (с помощью уравнений состояния и термодинамических соотношений) методы определения свойств в зависимости от рассматриваемого процесса и требуемой точности расчета. Все термодинамические процессы можно рассчитать с помощью таблиц, но при этом приходится много интерполировать. Поэтому иногда сочетают два метода: часть свойств определяют по таблицам, а часть – по диаграммам. В последнее время всё чаще применяют аналитический метод расчёта термодинамических свойств рабочих тел непосредственно по их уравнениям состояния на ЭВМ с использованием термодинамических соотношений. Такой метод особенно эффективен при оптимизационных расчетах циклов паротурбинных и холодильных установок, когда приходится многократно определять с высокой точностью и, главное, с внутренней согласованностью, термодинамические свойства рабочих тел. Важной особенностью процессов в реальном газе является возможность их протекания, как в однофазной так и в двухфазной области (влажный пар) либо последовательно в двух областях состояния. В связи с этим необходимо определять с помощью таблиц либо диаграмм к какой области относятся начальное и конечное состояния рабочего тела, совершающего термодинамический процесс. Это обстоятельство обуславливает необходимость использования таблиц для однофазной области либо для состояния насыщения и известных аддитивных формул для расчета свойств влажного пара. При расчетах термодинамических процессов в реальном газе встречаются следующие случаи: – начальное и конечное состояния находятся в однофазной области (пар либо жидкость), причем процесс может проходить через двухфазную область, то есть начинаться в жидкости и оканчиваться в паре (либо наоборот). В этом случае задача решается с помощью таблиц термодинамических свойств жидкости и перегретого пара; – начальное и конечное состояния находятся в двухфазной области. Тогда используют только таблицы свойств насыщенных жидкости и пара и аддитивные формулы для расчета свойств влажного пара; – процесс начинается в однофазной области (жидкости либо паре), а заканчивается в двухфазной области (либо наоборот). В таком случае термодинамические свойства в однофазной области определяют по таблицам для жидкости либо перегретого пара, а в двухфазной области рассчитывают по аддитивным формулам, используя таблицы для состояния насыщения. В большинстве перечисленных случаев можно определять свойства и рассчитывать процессы с помощью диаграмм состояния, но при этом надо учитывать, что на диаграмме h,s для воды и водяного пара отсутствуют пограничная кривая насыщенной жидкости и область жидкости. Ниже приводятся примеры расчета и анализа процессов, протекающих в воде и водяном паре при постоянных значениях термических параметров (удельного объёма, давления и температуры), а затем более сложных процессов, совершающиеся при постоянных значениях калорических свойств (адиабатного (изоэнтропного) и процесса дросселирования). В конце раздела подробно рассмотрен процесс течения пара – основной рабочий процесс паротурбинных установок.
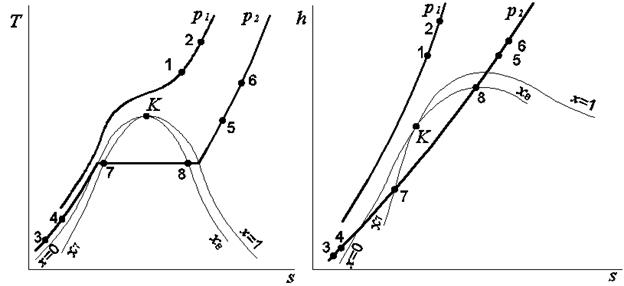
Изохорный процесс На рис. 3.1 изображены в координатах T,s и h,s две изохоры: v 1 = idem и v 2 = idem (v 2 >v 1 ) . На этих изохорах указаны восемь точек. Точки 1, 2, 5 и 6 соответствуют состоянию перегретого пара, точки 3, 4 – состоянию обычной и кипящей (насыщенной) жидкости, наконец, точки 7, 8 – влажному пару. В соответствии с указанным расположением точек могут быть идентифицированы следующие варианты изохорного процесса: - 1-2 и 5-6 – процессы, протекающие в области перегретого пара; - 3-4 – процесс, протекающий в области жидкости; - 3 - 4-7 – процесс с фазовым переходом жидкость – влажный пар; - 7-8 – процесс в области влажного пара; - 8-5 – процесс с фазовым переходом влажный пар – перегретый пар. Рассмотрим примеры решения задач, в которых рабочее тело совершает изохорный процесс.
Задача 1 Определить фазовое состояние и термодинамические свойства воды либо водяного пара, если температура вещества 200 °С, а удельный объём 0,12 м3/кг. Задачу решить с помощью диаграммы h,s, а затем уточнить по таблицам свойств воды и водяного пара (табл. 1 Приложения).
Рис. 3.1. Изображение изохорных процессов на энтропийных диаграммах Решение задачи с помощью диаграммы h,s Находим точку пересечения изотермы 200 °С (на цветной диаграмме h,s обычно красная линия) с пограничной кривой х = 1 (рис. 3.2) и определяем давление насыщения p s= р 8= 1,55 МПа. Далее в пересечении изобары р 8 (чёрная линия) с изохорой v = 0,12 м3/кг (зелёная линия) находим искомую точку 8. Она находится ниже и слева от пограничной кривой х = 1 и соответствует состоянию влажного пара, которое характеризируется в данном случае: степенью сухости х 8 = 0,94, энтальпией h 8 = 2680 кДж/кг, энтропией s 8 = 6,2 кДж/(кг·К) (определение значений х 8, h 8 и s 8 показано стрелками, исходящими из точки 8).
Решение задачи с помощью таблицы свойств воды и водяного пара в состоянии насыщения (табл. 1 Приложения) Из табл.1 видно, что при t 1 = 200 °С удельный объём насыщенной жидкости v' = 0,00116 м3/кг, а удельный объём насыщенного пара v ''= 0,12714 м3/кг, то есть v’< v8< v’’, что соответствует состоянию влажного пара. Тогда степень сухости влажного пара х 8 рассчитывается из тождества
Рис. 3.2. Определение состояния пара по заданным значениям температуры и удельного объема с помощью диаграммы h,s
Из первого равенства этого тождества рассчитываем степень сухости
Зная величину х 8, вычисляем из уравнений, полученных из указанного тождества, значения энтальпии h 8 и энтропии s 8
Сопоставляя значения параметров х, h и s, определённых по диаграмме и по таблицам, можно сделать вывод, что они хорошо согласуются между собой. Задача 2. Определить количество теплоты, которое необходимо подвести к 1 кгвлажного пара, находящемуся в состоянии, характеризуемому точкой 8 (см. предыдущую задачу), чтобы его изохорно перевести в состояние перегретого пара с температурой t 5 = 300 °С (точка 5, рис.3.3). Задачу решить с помощью диаграммы h,s, а затем уточнить по таблицам свойств воды и водяного пара ([3], табл. III).
Решение задачи с помощью диаграммы h,s
Рис. 3.3. Определение состояния перегретого пара с помощью диаграммы h,s при заданных значениях t и v На пересечении изохоры v 8 = 0,12 м3/кг (зелёная линия) с изотермой t 5 = 300 °С (красная линия) находим точку 5, в которой давление равно 2,1 МПа (ри.3.3). Определяем калорические свойства перегретого пара в этой точке(показано стрелками): энтальпия h 5 = 3020 кДж/кг; энтропия s 5 = 6, 75 кДж/(кг·К). Теплота в изохорном процессе расходуется только на изменение внутренней энергии и рассчитывается из соотношения
Тогда
Решение задачи с помощью таблиц термодинамических свойств воды и водяного пара [3]. Поскольку на диаграмме h,s изохора круче изобары, искомая точка 5 на изотерме 300 °Св области перегретого пара находится при более высоком давлении, чем давление в точке 8 р 8 = 15,5 бар. Поэтому в таблицах свойств воды и водяного пара ([3], стр.110) при р > р 8 ищем две смежные изобары, на которых удельные объёмы при t = 300 °С образуют интервал для заданного удельного объёма v 5 = v 8 = 0,12 м3/кг. Такими являются изобары 20 бар и 21 бар, термодинамические свойства на которых при t = 300 °C равны
p б = 20 бар p м = 21 бар v б= 0,1255 м3/кг v м= 0,1192 м3/кг h б= 3024 кДж/кг h м= 3021,1 кДж/кг s б = 6,7679 кДж/(кг·К) s м= 6,7416 кДж/(кг·К)
(свойствам приписаны символы «б» и «м» (большее и меньшее) в зависимости от значения v на соответствующей изобаре по сравнению с v 5 = v 8 = 0,12 м3/кг). Интерполируем по v (определяем коэффициент интерполяции kv)
Используя найденное значение kv, рассчитываем свойства в точке 5 - давление
- энтальпию
- энтропию
Тогда – внутренняя энергия перегретого пара в точке 5
– внутренняя энергия влажного пара в точке 8
Теплота, подводимая в изохорном процессе 8-5
Таким образом, результаты определения параметров пара в точке 5 и расчета теплоты, подводимой в процессе 8-5,по диаграмме и таблицам согласуются вполне удовлетворительно, учитывая возможную точность определения энтальпии h по диаграмме h,s (1мм = 4 кДж/кг).
Изобарный процесс На рис. 3.4. изображены в координатах T,s и h,s две изобары: одна (р 1 = idem) – докритическая, а вторая (р 2 = idem) – сверхкритическая, то есть р 2 >р 1. На изобарах отмечены восемь точек, из них точки 1, 2, 5 и 6 находятся в состоянии перегретого пара, 3 и 4 – в состоянии жидкости), 7 и 8 – в двухфазной области (влажный пар).
Рис. 3.4. Изображение изобарных процессов на энтропийных диаграммах Используя принятые обозначения точек, выделим возможные варианты изобарного процесса: – 1-2 и 5-6 – процессы, протекающие в области перегретого пара; – 3-4 – процесс в области жидкости; – 4-7 – процесс с фазовым переходом жидкость – влажный пар; – 7-8 – процесс в области влажного пара; – 8-5 – процесс с фазовым переходом влажный пар – перегретый пар. Рассмотрим примеры решения задач. Задача 1 Определить фазовое состояние и термодинамические свойства водяного пара, если его давление 10 бар, а удельный объём 0,12 м3/кг. Задачу решить с помощью диаграммы h,s, а затем уточнить по таблицам свойств воды и водяного пара (табл. 1 Приложения). Решение задачи с помощью диаграммы h,s Находим точку пересечения изобары р = 1,0 МПа на диаграмме h,s (черная линия) с изохорой v = 0,12 м3/кг (зелёная линия). Это и есть искомая точка, которую обозначим цифрой 8 (рис. 3.5). Поскольку данная точка находится левее и ниже пограничной кривой насыщенного пара (х = 1), она соответствует состоянию влажного пара со степенью сухости х 8 = 0,6, которое характеризируется следующими калорическими свойствами: энтальпия h 8 = 2000 кДж/кг; энтропия s 8 = 4,87 кДж/(кг·К). Определение значений h 8 и s 8 показано стрелками, исходящими из точки 8.
Рис. 3.5. Определение состояния пара с помощью диаграммы h,s
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 552; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.01 с.) |


 .
.
 .
. ,
, .
.
 ,
,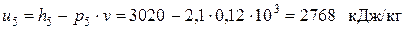 ,
,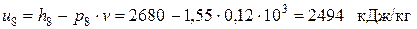 .
. .
. .
.
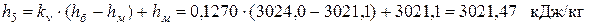
 .
.
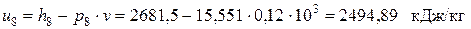 .
. .
.