
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистический и термодинамический методы. Опытные законы идеального газаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Статистический и термодинамический методы исследования. Молекулярная физика и термодинамика — разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (молекулярно-кинетический) и термодинамический. Первый лежит в основе молекулярной физики, второй — термодинамики. Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении. Идея об атомном строении вещества высказана древнегреческим философом Демокритом (460—370 до н. э.). Атомистика возрождается вновь лишь в XVII в. и развивается в работах М. В. Ломоносова, взгляды которого на строение вещества и тепловые явления были близки к современным. Строгое развитие молекулярной теории относится к середине XIX в. и связано с работами немецкого физика Р. Клаузиуса (1822—1888), Дж. Максвелла и Л. Больцмана. Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энергии и т. д.). Например, температура тела определяется скоростью хаотического движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул. Термодинамика — раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных законах, установленных в результате обобщения опытных данных. Область применения термодинамики значительно шире, чем молекулярно-кинетической теории, ибо нет таких областей физики и химии, в которых нельзя было бы пользоваться термодинамическим методом. Однако, с другой стороны, термодинамический метод несколько ограничен: термодинамика ничего не говорит о микроскопическом строении вещества, о механизме явлений, а лишь устанавливает связи между макроскопическими свойствами вещества. Молекулярно-кинетическая теория и термодинамика взаимно дополняют друг друга, образуя единое целое, но отличаясь различными методами исследования. Термодинамика имеет дело с термодинамической системой — совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой). Основа термодинамического метода — определение состояния термодинамической системы. Состояние системы задается термодинамическими параметрами (параметрами состояния) — совокупностью физических величин, характеризующих свойства термодинамической системы. Обычно в качестве параметров состояния выбирают температуру, давление и удельный объем. Температура — одно из основных понятий, играющих важную роль не только в термодинамике, но и в физике в целом. Температура — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. В соответствии с решением XI Генеральной конференции по мерам и весам (1960) в настоящее время можно применять только две температурные шкалы — термодинамическую и Международную практическую, градуированные соответственно в кельвинах (К) и в градусах Цельсия (°С). В Международной практической шкале температура замерзания и кипения воды при давлении 1,013×105 Па соответственно 0 и 100°С (реперные точки). Термодинамическая температурная шкала определяется по одной реперной точке, в качестве которой взята тройная точка воды (температура, при которой лед, вода и насыщенный пар при давления 609 Па находятся в термодинамическом равновесии). Температура этой точки по термодинамической шкале равна 273,16 К (точно). Градус Цельсия равен кельвину. В термодинамической шкале температура замерзания воды равна 273,15 К (при том же давлении, что и в Международной практической шкале), поэтому, по определению, термодинамическая температура и температура по Международной практической шкале связаны соотношением Т = 273,15 + t. Температура T = 0 К называется нулем кельвин. Анализ различных процессов показывает, что 0 К недостижим, хотя приближение к нему сколь угодно близко возможно. Удельный объем v — это объем единицы массы. Когда тело однородно, т. е. его плотность r = const, то v=V/m= 1 /p. Так как при постоянной массе удельный объем пропорционален общему объему, то макроскопические свойства однородного тела можно характеризовать объемом тела. Параметры состояния системы могут изменяться. Любое изменение в термодинамической системе, связанное с изменением хотя бы одного из ее термодинамических параметров, называется термодинамическим процессом. Макроскопическая система находится в термодинамическом равновесии, если ее состояние с течением времени не меняется (предполагается, что внешние условия рассматриваемой системы при этом не изменяются). В молекулярно-кинетической теории пользуются идеализированной моделью идеального газа, согласно которой считают, что: 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; 2) между молекулами газа отсутствуют силы взаимодействия; 3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие. Модель идеального газа можно использовать при изучении реальных газов, так как они в условиях, близких к нормальным (например, кислород и гелий), а также при низких давления» и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки, учитывающие собственный объем молекул газа и действующие молекулярные силы, можно перейти к теории реальных газов. Рассмотрим законы, описывающие поведение идеальных газов. Закон Бойля—Мариотта: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная: pV=const при T=const, m=const. (33.1) Кривая, изображающая зависимость между величинами р и V, характеризующими свойства вещества при постоянной температуре, называется изотермой. Изотермы представляют собой гиперболы, расположенные на графикетем выше, чем выше температура, при которой происходит процесс (рис. 60).
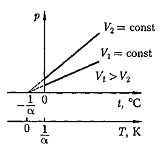
Рис. 60 Законы Гей-Люссака:1) объем данной массы газа при постоянном давлении изменяется линейно с температурой: V = V0(1+ 2) давление данной массы газа при постоянном объеме изменяется линейно с температурой: p = p0(1+ В этих уравнениях t — температура по шкале Цельсия, р 0 и V 0 — давление и объем при 0°С, коэффициент a = 1/273,15 К–1. Процесс, протекающий при постоянном давлении, называется изобарным. На диаграмме в координатах V, t (рис. 61) этот процесс изображается прямой, называемой изобарой. Процесс, протекающий при постоянном объеме, называется изохорным. На диаграмме в координатах р, t (рис. 62) он изображается прямой, называемой изохорой.
Рис. 62 Рис. 61
Из (33.2) и (33.3) следует, что изобары и изохоры пересекают ось температур в точке t=– 1 /a=– 273,15°С, определяемой из условия 1+a t = 0. Если перенести начало отсчета в эту точку, то происходит переход к шкале Кельвина (рис. 62), откуда T = t + 1/a Вводя в формулы (41.2) и (41.3) термодинамическую температуру, законам Гей-Люссака можно придать более удобный вид: V = V0(1+ p = p0(1+ V1/V2 = T1/T2 при p = const, m =const; (33.4) p1/p2 = T1/T2 при V = const, m= const; (33.4) где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре. Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях этот объем равен 22,41×10–3 м3/моль. По определению, в одном моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро:
Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений p 1 ,p 2 ,..., рn входящих в нее газов:
Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.
§ 34. Уравнение Клапейрона — Менделеева Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р, объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде дается выражением
где каждая из переменных является функцией двух других. Французский физик и инженер Б. Клапейрон (1799—1864) вывел уравнение состояния идеального газа, объединив законы Бойля — Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V 1, имеет давление р 1 и находится при температуре T 1. Эта же масса газа в другом произвольном состоянии характеризуется параметрами р 2, V 2, T 2 (рис. 63). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: 1) изотермического (изотерма 1–1'), 2) изохорного (изохора 1'–2).
Рис. 63 В соответствии с законами Бойля — Мариотта (41.1) и Гей-Люссака (41.5) запишем:
Исключив из уравнений (34.1) и (34.2)
Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа величина pV/T остается постоянной, т. е.
Выражение (34.3) является уравнением Клапейрона, в котором В — газовая постоянная, различная для разных газов. Русский ученый Д. И. Менделеев (1834—1907) объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (42.3) к одному молю, использовав молярный объем V m. Согласно закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем V m, поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярном газовой постоянной. Уравнению
удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона — Менделеева. Числовое значение молярной газовой постоянной определим из формулы (34.4), полагая, что моль газа находится при нормальных условиях (р 0 = 1,013×105 Па, T 0=273,15 К, V m=22,41×10–3 м3/моль): R =8,31 Дж/(моль×К). От уравнения (42.4) для моля газа можно перейти к уравнению Клапейрона — Менделеева для произвольной массы газа. Если при некоторых заданных давлении и температуре один моль газа занимает молярный объем V m, то при тех же условиях масса т газа займет объем V= (т/М)V m, где М — молярная масса (масса одного моля вещества). Единица молярной массы — килограмм на моль (кг/моль). Уравнение Клапейрона — Менделеева для массы т газа
где n =m/M — количество вещества. Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана:
Исходя из этого уравнение состояния (42.4) запишем в виде
где N A /V m = n — концентрация молекул (число молекул в единице объема). Таким образом, из уравнения
следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м3 газа при нормальных условиях, называется числом Лошмидта:
|
||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 1498; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |


 t) при p=const, m=const; (33.2)
t) при p=const, m=const; (33.2)




 (34.1)
(34.1) (34.2)
(34.2) получим
получим
 (34.3)
(34.3) (34.4)
(34.4) (34.5)
(34.5)
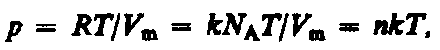
 (34.6)
(34.6)



