
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение теоремы Гаусса к расчету некоторых электростатических полей в вакуумеСодержание книги
Поиск на нашем сайте
1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 126) заряжена с постоянной поверхностной плотностью +s(s = d Q/ d S — заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (соsa=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равенсумме потоков сквозь его основания (площади оснований равны и для основания Еn совпадает с Е), т. е. равен 2 ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен s S. Согласно теореме Гаусса (81.2), 2 ES= s S/ e0, откуда
Из формулы (56.1) вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.
Рис. 126 Рис. 127
2. Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 127). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями + sи –s. Поле таких плоскостей найдемкак суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля E =0. В области между плоскостями E = E + + E – (E + и E – определяются по формуле (56.1)), поэтому результирующая напряженность
Таким образом, результирующая напряженность поля в области между плоскостями описывается формулой (56.2), а вне объема, ограниченного плоскостями, равна нулю. 3. Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +s. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (рис. 128). Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R,ro внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса (55.2),
При r>R поле убывает с расстоянием r по такому же закону,как у точечного заряда. График зависимости Е от r приведен на рис. 129. Если r'<R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E =0).
Рис 128 Рис. 129 4. Поле объемно заряженного шара. Шар радиуса R с общим зарядом Q заряжен равномерно собъемной плотностью r(r =
Таким образом, напряженность поля вне равномерно заряженного шара описывается формулой (56.3), а внутри его изменяется линейно с расстоянием r' согласно выражению (56.4). График зависимости Е от r для рассмотренного случая приведен на рис. 130.
Рис. 130 5. Поле равномерно заряженного бесконечного цилиндра (нити). Бесконечный цилиндр радиуса R (рис. 131) заряжен равномерно с линейной плотностью t (t =
Рис. 131
напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса r и высотой l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность равен 2 prlЕ. По теореме Гаусса (55.2), при r>R 2 prlЕ = tl/e 0, откуда
Если r<R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области E =0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением (56.5), внутри же его поле отсутствует.
§ 57. Циркуляция вектора напряженности электростатического поля Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории (рис. 132) перемещается другой точечный заряд Q 0, то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении d l равна
Рис. 132
Так как dcosa=d r, то
Работа при перемещении заряда Q 0 из точки 1 в точку 2
не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы — консервативными (см. § 11). Из формулы (57.1) следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е.
Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути d l равна Е d l = El dl, где El = E cos a — проекция вектора Е на направление элементарного перемещения. Тогда формулу (53.2) можно записать в виде
Интеграл Формула (57.3) справедлива только для электростатического поля. В дальнейшем будет показано, что для поля движущихся зарядов условие (57.3) не выполняется (для него циркуляция вектора напряженности отлична от нуля).
§ 58. Потенциал электростатического поля Тело, находящееся в потенциальном поле сил (а электростатическое поле является потенциальным), обладает потенциальной энергией, за счет которой силами поля совершается работа (см. § 11). Как известно (см. (11.2)), работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу (57.1) сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q 0 в начальной и конечной точках поля заряда Q:
откуда следует, что потенциальная энергия заряда q0 в поле заряда Q равна
Она, как и в механике, определяется неоднозначно, а с точностью до произвольной постоянной С. Если считать, что при удалении заряда в бесконечность (r ®¥) потенциальная энергия обращается в нуль (U =0), то С =0 и потенциальная энергия заряда Q 0, находящегося в поле заряда Q на расстоянии г от него, равна
Для одноименных зарядов Q 0 Q> 0 и потенциальная энергия их взаимодействия (отталкивания) положительна, для разноименных зарядов Q 0 Q <0 и потенциальная энергия их взаимодействия (притяжения) отрицательна. Если поле создается системой n точечных зарядов Q 1, Q 2 ,..., Qn, то работа электростатических сил, совершаемая над зарядом Q 0, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия U заряда Q 0, находящегося в этом поле, равна сумме потенциальных энергий Ui, каждого из зарядов:
Из формул (58.2) и (58.3) вытекает, что отношение U/Q 0 не зависит от Q 0 и является поэтому энергетической характеристикой электростатического поля, называемой потенциалом:
Потенциал j в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку. Из формул (58.4) и (58.2) следует, что потенциал поля, создаваемого точечным зарядом Q, равен
Работа, совершаемая селами электростатического поля при перемещении заряда Q 0 из точки 1 в точку 2 (см. (58.1), (58.4), (58.5)), может быть представлена как
т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках. Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного положительного заряда из точки 1 в точку 2. Работа сил поля при перемещении заряда Q 0 из точки 1 в точку 2 может быть записана также в виде
Приравняв (58.6) и (58.7), придем к выражению для разности потенциалов:
где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения. Если перемещать заряд Q 0 из произвольной точки за пределы поля, т. е. в бесконечность, где, по условию, потенциал равен нулю, то работа сил электростатического поля, согласно (58.6), A ¥ =Q 0 j, откуда
Таким образом, потенциал — физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля. Из выражения (58.4) следует, что единица потенциала — вольт (В): 1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл). Учитывая размерность вольта, можно показать, что введенная в § 79 единица напряженности электростатического поля действительно равна 1 В/м: 1 Н/Кл=1 Н×м/(Кл×м)=1 Дж/(Кл×м)=1 В/м. Из формул (58.3) и (58.4) вытекает, что если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:
§ 59. Напряженность как градиент потенциала. Эквипотенциальные поверхности Найдем взаимосвязь между напряженностью электростатического поля, являющейся его силовой характеристикой, и потенциалом — энергетической характеристикой поля. Работа по перемещению единичного точечного положительного заряда из одной точки поля в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и x 2 —x 1 = d x, равна Ex d x. Та же работа равна j 1 —j 2 =dj. Приравняв оба выражения, можем записать
где символ частной производной подчеркивает, что дифференцирование производится только по х. Повторив аналогичные рассуждения для осей у и z, можем найти вектор Е:
где i, j, k — единичные векторы координатных осей х, у, z. Из определения градиента (11.4) и (11.6) следует, что
т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала. Для графического изображения распределения потенциала электростатического поля,как и в случае поля тяготения (см. § 24), пользуются эквипотенциальными поверхностями — поверхностями, во всех точках которых потенциал j имеет одно и то же значение. Если поле создается точечным зарядом, то его потенциал, согласно (58.5), Линии напряженности всегда нормальны к эквипотенциальным поверхностям. Действительно, все точки эквипотенциальной поверхности имеют одинаковый потенциал, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т. е. электростатические силы, действующие на заряд, всегда направлены по нормалям к эквипотенциальным поверхностям. Следовательно, вектор Е всегда нормален к эквипотенциальным поверхностям, а поэтому линии вектора Е ортогональны этим поверхностям.
Рис. 133
Эквипотенциальных поверхностей вокруг каждого заряда и каждой системы зарядов можно провести бесчисленное множество. Однако их обычно проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности расположены гуще, напряженность поля больше. Итак, зная расположение линий напряженности электростатического поля, можно построить эквипотенциальные поверхности и, наоборот, по известному расположению эквипотенциальных поверхностей можно определить в каждой точке поля модуль и направление напряженности поля. На рис. 133 для примера показан вид линий напряженности (штриховые линии) и эквипотенциальных поверхностей (сплошные линии) полей положительного точечного заряда (а) и заряженного металлического цилиндра, имеющего на одном конце выступ, а на другом — впадину (б).
§ 60. Вычисление разности потенциалов по напряженности поля Установленная в § 59 связь между напряженностью поля и потенциалом позволяет по известной напряженности поля найти разность потенциалов между двумя произвольными точками этого поля. 1. Поле равномерно заряженной бесконечной плоскости определяется формулой (56.1): E =s/(2e0), где s — поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях x 1 и х 2 от плоскости, равна (используем формулу (59.1))
2. Поле двух бесконечных параллельных разноименно заряженных плоскостей определяется формулой (56.2); Е= s/e0, где s — поверхностная плотность заряда. Разность потенциалов между плоскостями, расстояние между которыми равно d (см. формулу (59.1)), равна
3. Поле равномерно заряженной сферической поверхности радиуса R с общим зарядом Q вне сферы (r> R) вычисляется по (56.3):
Если принять r 1 =r и r 2=¥, то потенциал поля вне сферической поверхности, согласно формуле (60.2), задается выражением
(ср. с формулой (58.5)). Внутри сферической поверхности потенциал всюду одинаков и равен
График зависимости j от r приведен на рис. 134.
Рис. 134
4. Поле объемно заряженного шара радиуса R с общим зарядом Q вне шара (r>R) вычисляется по формуле (56.3), поэтому разность потенциалов между двумя точками, лежащими на расстояниях r 1 и r 2 от центра шара (r 1 > R, r 2 > R, r 2 > r 1), определяется формулой (60.2). В любой точке, лежащей внутри шара на расстоянии r ' от его центра (r'<R), напряженность определяется выражением (56.4):
5. Поле равномерно заряженного бесконечного цилиндра радиуса R, заряженного с линейной плотностью t, вне цилиндра (r>R) определяется формулой (56.5):
§ 61. Типы диэлектриков. Поляризация диэлектриков Диэлектрик (как и всякое вещество) состоит из атомов и молекул. Так как положительный заряд всех ядер молекулы равен суммарному заряду электронов, то молекула в целом электрически нейтральна. Если заменить положительные заряды ядер молекул суммарным зарядом + Q, находящимся в центре «тяжести» положительных зарядов, а заряд всех электронов — суммарным отрицательным зарядом – Q, находящимся в центре «тяжести» отрицательных зарядов, то молекулу можно рассматривать как электрический диполь с электрическим моментом, определяемым формулой (54.3). Первую группу диэлектриков (N2, Н2, О2, СО2, СН4,...) составляют вещества, молекулы которых имеют симметричное строение, т. е. центры «тяжести» положительных и отрицательных зарядов в отсутствие внешнего электрического поля совпадают и, следовательно, дипольный момент молекулы р равен нулю. Молекулы таких диэлектриков называются неполярными. Под действием внешнего электрического поля заряды неполярных молекул смещаются в противоположные стороны (положительные по полю, отрицательные против поля) и молекула приобретает дипольный момент. Вторую группу диэлектриков (H2O, NН3, SO2, CO,...) составляют вещества, молекулы которых имеют асимметричное строение, т. е. центры «тяжести» положительных и отрицательных зарядов не совпадают. Таким образом, эти молекулы в отсутствие внешнего электрического поля обладают дипольным моментом. Молекулы таких диэлектриков называются полярными. При отсутствии внешнего поля, однако, дипольные моменты полярных молекул вследствие теплового движения ориентированы в пространстве хаотично и их результирующий момент равен нулю. Если такой диэлектрик поместить во внешнее поле, то силы этого поля будут стремиться повернуть диполи вдоль поля и возникает отличный от нуля результирующий момент. Третью группу диэлектриков (NaCl, KCl, КВr,...) составляют вещества, молекулы которых имеют ионное строение. Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельные молекулы, а рассматривать их можно как систему двух вдвинутых одна в другую ионных подрешеток. При наложении на ионный кристалл электрического поля происходит некоторая деформация кристаллической решетки или относительное смещение подрешеток, приводящее к возникновению дипольных моментов. Таким образом, внесение всех трех групп диэлектриков во внешнее электрическое поле приводит к возникновению отличного от нуля результирующего электрического момента диэлектрика, или, иными словами, к поляризации диэлектрика. Поляризацией диэлектрика называется процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю диполей. Соответственно трем группам диэлектриков различают три вида поляризации: электронная, или деформационная, поляризация диэлектрика с неполярными молекулами, заключающаяся в возникновении у атомов индуцированного дипольного момента за счет деформации электронных орбит; ориентационная, или дипольная, поляризация диэлектрика с полярными молекулами, заключающаяся в ориентации имеющихся дипольных моментов молекул по полю. Естественно, что тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрическое поле и тепловое движение) возникает преимущественная ориентация дипольных моментов молекул по полю. Эта ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура; ионная поляризация диэлектриков с ионными кристаллическими решетками, заключающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицательных — против поля, приводящем к возникновению дипольных моментов.
§ 62. Поляризованность. Напряженность поля в диэлектрике При помещении диэлектрика во внешнее электрическое поле он поляризуется, т. е. приобретает отличный от нуля дипольный момент
Из опыта следует, что для большого класса диэлектриков (за исключением сегнетоэлектриков, см. § 65) поляризованность Р линейно зависит от напряженности поля Е. Если диэлектрик изотропный и Е не слишком велико, то
где æ — диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика; æ – величина безразмерная; притом всегда æ > 0 и для большинства диэлектриков (твердых и жидких) составляет несколько единиц (хотя, например, для спирта æ»25, для воды æ =80). Для установления количественных закономерностей поля в диэлектрике внесем в однородное внешнее электрическое поле Е 0 (создается двумя бесконечными параллельными разноименно заряженными плоскостями) пластинку из однородного диэлектрика, расположив ее так, как показано на рис. 135. Под действием поля диэлектрик поляризуется, т. е. происходит смещение зарядов: положительные смещаются по полю, отрицательные — против поля. В результате этого на правой грани диэлектрика, обращенного к отрицательной плоскости, будет избыток положительного заряда с поверхностной плотностью + s ', на левой — отрицательного заряда с поверхностной плотностью –s'. Эти нескомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называются связанными. Так как их поверхностная плотность s' меньше плотности s свободных зарядов плоскостей, то не все поле Е компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть — обрывается на связанных зарядах. Следовательно, поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика Е = Е 0.
Рис. 135
Таким образом, появление связанных зарядов приводит к возникновению дополнительного электрического поля Е ' (поля, создаваемого связанными зарядами), которое направлено против внешнего поля Е 0 (поля, создаваемого свободными зарядами) и ослабляет его. Результирующее поле внутри диэлектрика
Поле Е'=s'/e 0 (поле, созданное двумя бесконечными заряженными плоскостями; см. формулу (82.2)), поэтому
Определим поверхностную плотность связанных зарядов s'. По (62.1), полный дипольный момент пластинки диэлектрика pv =PV = PSd, где S — площадь грани пластинки, d — ее толщина. С другой стороны, полный дипольный момент, согласно (54.3), равен произведению связанного заряда каждой грани Q' =s' S на расстояние d между ними, т. е. рV = s' Sd. Таким образом, PSd= s' Sd, или
т. е. поверхностная плотность связанных зарядов s' равна поляризованности Р. Подставив в (62.3) выражения (62.4) и (62.2), получим
откуда напряженность результирующего поля внутри диэлектрика равна
Безразмерная величина
называется диэлектрической проницаемостью среды. Сравнивая (62.5) и (62.6), видим, что e показывает, во сколько раз поле ослабляется диэлектриком, и характеризует количественно свойство диэлектрика поляризоваться в электрическом поле.
§ 63. Электрическое смещение. Теореме Гаусса для электростатического поля в диэлектрике Напряженность электростатического поля, согласно (62.5), зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна e. Вектор напряженности Е, переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчетах электростатических полей. Поэтому оказалось необходимым помимо вектора напряженности характеризовать поле еще вектором электрического смещения, который для электрически изотропной среды, по определению, равен
Используя формулы (62.6) и (62.2), вектор электрического смещения можно выразить как
Единица электрического смещения — кулон на метр в квадрате (Кл/м2). Рассмотрим, с чем можно связать вектор электрического смещения. Связанные заряды появляются в диэлектрике при наличии внешнего электростатического поля, создаваемого системой свободных электрических зарядов, т. е. в диэлектрике на электростатическое поле свободных зарядов накладывается дополнительное поле связанных зарядов. Результирующее поле в диэлектрике описывается вектором напряженности Е, и потому он зависит от свойств диэлектрика. Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, возникающие в диэлектрике, могут вызвать, однако, перераспределение свободных зарядов, создающих поле. Поэтому вектор D характеризует электростатическое поле, создаваемое свободными зарядами (т. е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика. Аналогично, как и поле Е, поле D изображается с помощью линий электрического смещения, направление и густота которых определяются точно так же, как и для линий напряженности (см. §53). Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь. Для произвольной замкнутой поверхности S поток вектора D сквозь эту поверхность
где Dn — проекция вектора D на нормаль n к площадке d S. Теорема Гаусса для электростатического поля в диэлектрике:
т. е. поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред. Для вакуума Dn = e 0 En (e =1), тогда поток вектора напряженности Е сквозь произвольную замкнутую поверхность (ср. с (55.2)) равен
Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса (55.2) для поля Е в самом общем виде можно записать как
где
§ 64. Условия на границе раздела двух диэлектрических сред Рассмотрим связь между векторами Е и D на границе раздела двух однородных изотропных диэлектриков (диэлектрические проницаемости которых e1 и e2) при отсутствии на границе свободных зарядов. Построим вблизи границы раздела диэлектриков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA длины l, ориентировав его так, как показано на рис. 136.
Рис. 136
Согласно теореме (57.3) о циркуляции вектора Е,
откуда
(знаки интегралов по АВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DA ничтожно малы). Поэтому
Заменив, согласно (63.1), проекции вектора Е проекциями вектора D, деленными на e0e, получим
На границе раздела двух диэлектриков (рис. 137) построим прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом диэлектрике, другое — во втором. Основания D S настолько малы, что в пределах каждого из них вектор D одинаков.
Рис. 137 Рис. 138
Согласно теореме Гаусса (63.3),
(нормали n и n' к основаниям цилиндра направлены противоположно). Поэтому
Заменив, согласно (63.1), проекции вектора D проекциями вектора Е, умноженными на e0e, получим
Таким образом, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора Е (Еt) и нормальная составляющая вектора D (Dn) изменяются непрерывно (не претерпевают скачка), а нормальная составляющая вектора Е (En) и тангенциальная составляющая вектора D (Dt) претерпевают скачок. Из условий (64.1) — (64.4) для составляющих векторов Е и D следует, что линии этих векторов испытывают излом (преломляются). Найдем связь между углами a1 и a2 (на рис. 138 e1>e2). Согласно (64.1) и (64.4), Еt 2 = Еt 1 и e2 En 2 = e1 En 1. Разложим векторы E 1 и E 2 у границы раздела на тангенциальные и нормальные составляющие. Из рис. 138 следует, что
Учитывая записанные выше условия, получим закон преломления линий напряженности Е (а значит, и линий смещения D)
Эта формула показывает, что, входя в диэлектрик с большей диэлектрической проницаемостью, линии Е и D удаляются от нормали.
§ 65. Сегнетоэлектрики Сегнетоэлектрики — диэлектрики, обладающие в определенном интервале температур спонтанной (самопроизвольной) поляризованностью, т. е. поляризованностью в отсутствие внешнего электрического поля. К сегнетоэлектрикам относятся, например, детально изученные И. В. Курчатовым (1903—1960) и П. П. Кобеко (1897—1954) сегнетова соль NaKC4H4O6 • 4Н2О (от нее и получили свое название сегнетоэлектрики) и титанат бария ВаТiO3. При отсутствии внешнего электрического поля сегнетоэлектрик представляет собой как бы мозаикуиз доменов — областей с различными направлениями поляризованности. Это схематически показано на примере титаната бария (рис. 139), где стрелки и знаки
|
||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 2484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.015 с.) |

 (56.1)
(56.1)

 (56.2)
(56.2) , откуда
, откуда (56.3)
(56.3)
 –заряд, приходящийся на единицу объема). Учитывая соображения симметрии (см. п. 3), можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае (см. (56.3)). Внутри же шара напряженность поля будет другая. Сфера радиуса r'<R охватывает заряд Q'= 4/3
–заряд, приходящийся на единицу объема). Учитывая соображения симметрии (см. п. 3), можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае (см. (56.3)). Внутри же шара напряженность поля будет другая. Сфера радиуса r'<R охватывает заряд Q'= 4/3  . Поэтому, согласно теореме Гаусса (55.2),
. Поэтому, согласно теореме Гаусса (55.2),  . Учитывая, что
. Учитывая, что  , получаем
, получаем (56.4)
(56.4)
 – заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии
– заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии
 (56.5)
(56.5)


 (57.1)
(57.1) (57.2)
(57.2) (57.3)
(57.3) называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее свойством (57.3), называется потенциальным. Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.
называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее свойством (57.3), называется потенциальным. Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность. (58.1)
(58.1)
 (58.2)
(58.2) (58.3)
(58.3) (58.4)
(58.4) (58.5)
(58.5) (58.6)
(58.6) (58.7)
(58.7) (58.8)
(58.8) (58.9)
(58.9)
 (59.1)
(59.1)
 (59.2)
(59.2) Таким образом, эквипотенциальные поверхности в данном случае — концентрические сферы. С другой стороны, линии напряженности в случае точечного заряда — радиальные прямые. Следовательно, линии напряженности в случае точечного заряда перпендикулярны эквипотенциальным поверхностям.
Таким образом, эквипотенциальные поверхности в данном случае — концентрические сферы. С другой стороны, линии напряженности в случае точечного заряда — радиальные прямые. Следовательно, линии напряженности в случае точечного заряда перпендикулярны эквипотенциальным поверхностям.

 (60.1)
(60.1) Разностьпотенциалов между двумя точками, лежащими на расстояниях r 1 и r 2 от центра сферы (r 1 >R, r 2 >R, r 2 >r 1 ), равна
Разностьпотенциалов между двумя точками, лежащими на расстояниях r 1 и r 2 от центра сферы (r 1 >R, r 2 >R, r 2 >r 1 ), равна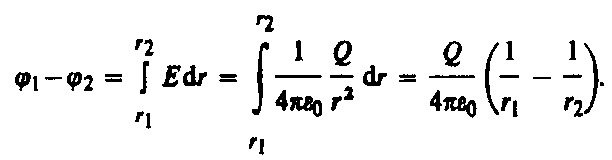 (60.2)
(60.2)


 Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях
Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях  и
и  от центра шара (
от центра шара (
 Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r 1 м r 2 от оси заряженного цилиндра (r 1> R, r 2> R, r 2> r 1), равна
Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r 1 м r 2 от оси заряженного цилиндра (r 1> R, r 2> R, r 2> r 1), равна (60.3)
(60.3) где р i — дипольный момент одной молекулы. Для количественного описания поляризации диэлектрика пользуются векторной величиной — поляризованностью, определяемой как дипольный момент единицы объема диэлектрика:
где р i — дипольный момент одной молекулы. Для количественного описания поляризации диэлектрика пользуются векторной величиной — поляризованностью, определяемой как дипольный момент единицы объема диэлектрика: (62.1)
(62.1) (62.2)
(62.2)

 (62.3)
(62.3) (62.4)
(62.4)
 (62.5)
(62.5) (62.6)
(62.6) (63.1)
(63.1) (63.2)
(63.2)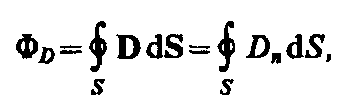
 (63.3)
(63.3)

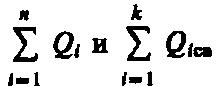 — соответственно алгебраические суммы свободных и связанных зарядов, охватываемых замкнутой поверхностью S. Однако эта формула неприемлема для описания поля Е в диэлектрике, так как она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз доказывает целесообразность введения вектора электрического смещения.
— соответственно алгебраические суммы свободных и связанных зарядов, охватываемых замкнутой поверхностью S. Однако эта формула неприемлема для описания поля Е в диэлектрике, так как она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз доказывает целесообразность введения вектора электрического смещения.


 (64.1)
(64.1) (64.2)
(64.2)

 (64.3)
(64.3) (64.4)
(64.4)

 , Å указывают направление вектора Р. Так как в смежных доменах эти направления различны, то в целом дипольный момент диэлектрика равен нулю. При внесении сегнетоэлектрика во внешнее поле происходит переориентация дипольных моментов доменов по полю, а возникшее при этом сумм
, Å указывают направление вектора Р. Так как в смежных доменах эти направления различны, то в целом дипольный момент диэлектрика равен нулю. При внесении сегнетоэлектрика во внешнее поле происходит переориентация дипольных моментов доменов по полю, а возникшее при этом сумм 


