
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. Статистическая термодинамика.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
II. Статистическая термодинамика. Основные понятия Квазистатический процесс; нулевой постулат феноменологической термодинамики; первый постулат феноменологической термодинамики; второй постулат феноменологической термодинамики; третий постулат феноменологической термодинамики; понятие внутренней энергии; функция состояния; функция процесса; основное термодинамическое равенство; понятие энтропии для изолированной неравновесной системы; понятие локальной неустойчивости фазовых траекторий (траекторий частиц); системы с перемешиванием; обратимый процесс; необратимый процесс; термодинамический потенциал; свободная энергия Гельмгольца; свободная энергия Гиббса; соотношения Максвелла; обобщённые координаты и обобщённые силы; принципы экстремума в термодинамике; принцип Ле-Шателье-Брауна.
Основные знания. Статистическая интерпретация понятий: внутренняя энергия, работа подсистемы, количество теплоты; обоснование первого начала термодинамики с помощью канонического распределения Гиббса; статистическое обоснование третьего термодинамики; свойства макросистем при
Основные умения. Самостоятельно работать с рекомендованной литературой; определять понятия из п.1; уметь логично обосновывать с использованием математического аппарата элементы знаний из п.2; по известной статистической сумме (статистическому интегралу) определять внутреннюю энергию системы, свободную энергию Гельмгольца, свободную энергию Гиббса, энтропию, уравнение состояния и т.п.; определять направление эволюции открытой системы при постоянных Внутренняя энергия макроскопической системы. Основой статистической термодинамики является следующее утверждение: внутренняя энергия макроскопического тела тождественна её средней энергии
Подставляя каноническое распределение Гиббса, получаем:
Числитель правой части равенства (2.2.2) представляет собой производную от Z по
Поэтому выражение (2.2.2) можно переписать в более компактном виде:
Таким образом, для нахождения внутренней энергии системы достаточно знать её статистическую сумму Z.
Второе начало термодинамики и «стрела времени». Энтропия изолированной системы в неравновесном состоянии. Если система находится в равновесном состоянии или участвует в квазистатическом процессе, её энтропия с молекулярной точки зрения определяется числом микросостояний, соответствующих данному макросостоянию системы с энергией, равной среднему значению:
Энтропия изолированной системы в неравновесном состоянии определяется числом микросостояний, соответствующих данному макросостоянию системы:
причём Третий закон термодинамики. Третий закон термодинамики характеризует свойства термодинамической системы при очень низких температурах (
Вопросы для самопроверки. 1. Сформулировать постулаты феноменологической термодинамики. 2. Сформулировать второй принцип термодинамики. 3. В чём заключается мысленный эксперимент Нарликара? 4. Доказать, что энтропия изолированной системы при неравновесных процессах возрастает. 5. Понятие внутренней энергии. 6. При каких условиях (в каких случаях) состояние системы можно рассматривать как равновесное? 7. Какой процесс называется обратимым и необратимым? 8. Что такое термодинамический потенциал? 9. Записать термодинамические функции. 10. Объяснить получение низких температур при адиабатическом размагничивании. 11. Понятие об отрицательной температуре. 12. Запишите термодинамические параметры через сумму состояний. 13. Записать основное термодинамическое равенство системы с переменным числом частиц. 14. Объяснить физический смысл химического потенциала.
Задачи.
1. Доказать основное термодинамическое равенство. 2. Найти выражение термодинамического потенциала свободной энергии F через интеграл состояния Z системы. 3. Найти выражение энтропии S через интеграл состояний Z системы. 4. Найти зависимость энтропия S идеального одноатомного газа из N частиц от энергии Е и объёма V. 5. Вывести основное термодинамическое равенство для системы с переменным числом частиц. 6. Вывести большое каноническое распределение. 7. Вычислить свободную энергию одноатомного идеального газа.
II. Статистическая термодинамика. Основные понятия Квазистатический процесс; нулевой постулат феноменологической термодинамики; первый постулат феноменологической термодинамики; второй постулат феноменологической термодинамики; третий постулат феноменологической термодинамики; понятие внутренней энергии; функция состояния; функция процесса; основное термодинамическое равенство; понятие энтропии для изолированной неравновесной системы; понятие локальной неустойчивости фазовых траекторий (траекторий частиц); системы с перемешиванием; обратимый процесс; необратимый процесс; термодинамический потенциал; свободная энергия Гельмгольца; свободная энергия Гиббса; соотношения Максвелла; обобщённые координаты и обобщённые силы; принципы экстремума в термодинамике; принцип Ле-Шателье-Брауна.
Основные знания. Статистическая интерпретация понятий: внутренняя энергия, работа подсистемы, количество теплоты; обоснование первого начала термодинамики с помощью канонического распределения Гиббса; статистическое обоснование третьего термодинамики; свойства макросистем при
Основные умения. Самостоятельно работать с рекомендованной литературой; определять понятия из п.1; уметь логично обосновывать с использованием математического аппарата элементы знаний из п.2; по известной статистической сумме (статистическому интегралу) определять внутреннюю энергию системы, свободную энергию Гельмгольца, свободную энергию Гиббса, энтропию, уравнение состояния и т.п.; определять направление эволюции открытой системы при постоянных
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.68.39 (0.01 с.) |

 ; физический смысл энтропии; условия устойчивости термодинамической системы.
; физический смысл энтропии; условия устойчивости термодинамической системы. и
и  , постоянных
, постоянных  и
и  .
. , вычисленной по законам статистической физики:
, вычисленной по законам статистической физики: (2.2.1)
(2.2.1) (2.2.2)
(2.2.2) :
: .
. (2.2.3)
(2.2.3) .
.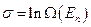 , (2.4.1.а)
, (2.4.1.а) .
. , а энергия возбуждённых состояний –
, а энергия возбуждённых состояний –  . При очень низкой температуре средняя энергия теплового движения
. При очень низкой температуре средняя энергия теплового движения 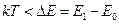 . Следовательно, энергии теплового движения недостаточно для перехода системы в возбуждённое состояние
. Следовательно, энергии теплового движения недостаточно для перехода системы в возбуждённое состояние  . Энтропия
. Энтропия 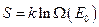 , где
, где  – число состояний системы с энергией
– число состояний системы с энергией  – очень маленькое число). Поскольку энтропия определяется с точностью до произвольной постоянной иногда это утверждение формулируют так: при
– очень маленькое число). Поскольку энтропия определяется с точностью до произвольной постоянной иногда это утверждение формулируют так: при  . Значение этой постоянной не зависит от давления, объёма и других параметров, характеризующих состояние системы.
. Значение этой постоянной не зависит от давления, объёма и других параметров, характеризующих состояние системы.


