
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внутренняя энергия макроскопической системы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основой статистической термодинамики является следующее утверждение: внутренняя энергия макроскопического тела тождественна её средней энергии
Подставляя каноническое распределение Гиббса, получаем:
Числитель правой части равенства (2.2.2) представляет собой производную от Z по
Поэтому выражение (2.2.2) можно переписать в более компактном виде:
Таким образом, для нахождения внутренней энергии системы достаточно знать её статистическую сумму Z.
Первое начало термодинамики. До сих пор мы говорили о состоянии системы (на микро- или макроуровнях) в какой-то определённый момент времени. Перейдём к рассмотрению процессов. Термодинамические параметры, можно разделить на внешние и внутренние. Внешние параметры характеризуют внешние условия, в которых находится система. Изменение этих параметров будем считать настолько медленными, что в каждый момент времени состояние системы можно рассматривать как равновесное. Такие процессы называются квазистатическими. Они обратимы. Если внешние параметры или температура термостата проходят через те же значения в обратном порядке, то и система проходит через те же равновесные состояния в обратном порядке. Из выражения (2.2.1) следует, что изменение внутренней энергии макроскопической системы можно представить в виде:
Здесь
При этом распределение вероятностей микросостояний остаётся неизменным. Величина
Здесь
есть работа, производимая над подсистемой при изменении внешних параметров
зависит от пути интегрирования. Нельзя определить работу, зная только начальное и конечное состояние системы, она не является функцией состояния. Второе слагаемое в соотношении (2.2.4) преобразуем следующим образом:
Поскольку Подставляем последнее выражение в (2.2.6):
Для макроскопической системы: Следовательно Если энергетические уровни системы остаются неизменными (внешние параметры не меняются), то энергия, подводимая к системе или отдаваемая ею, идёт на изменение распределения вероятностей микросостояний. Изменение энергии подсистемы возникает вследствии непосредственного взаимодействия частиц среды и подсистемы. Эту часть изменения энергии называют количеством теплоты
Для квазистатических процессов:
Подставляя (2.2.5) и (2.2.7) в соотношение (2.2.4) находим полное изменение внутренней энергии системы:
Для квазистатических процессов
Это одно из важнейших термодинамических соотношений. Количество теплоты Второе начало термодинамики и «стрела времени».
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 700; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.172.250 (0.007 с.) |

 , вычисленной по законам статистической физики:
, вычисленной по законам статистической физики: (2.2.1)
(2.2.1) (2.2.2)
(2.2.2) :
: .
. (2.2.3)
(2.2.3) (2.2.4)
(2.2.4) – изменение энергетических уровней системы при очень малом изменении её внешних параметров
– изменение энергетических уровней системы при очень малом изменении её внешних параметров  :
: .
. – сила, действующая на систему при изменении i -ого энергетического уровня вследствие изменения параметра
– сила, действующая на систему при изменении i -ого энергетического уровня вследствие изменения параметра  . Подставляя
. Подставляя  в первое слагаемое правой части соотношения (2.2.4), получаем:
в первое слагаемое правой части соотношения (2.2.4), получаем: .
. – средняя обобщенная сила, действующая на подсистему при изменении параметра
– средняя обобщенная сила, действующая на подсистему при изменении параметра  (2.2.5)
(2.2.5)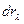 . Например, если
. Например, если 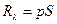 , где р – давление газа, S – площадь поршня. Тогда
, где р – давление газа, S – площадь поршня. Тогда  , где dV – изменение объёма подсистемы (газа в цилиндре).
, где dV – изменение объёма подсистемы (газа в цилиндре). 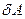 не является полным дифференциалом какого-либо выражения. Обобщённая сила
не является полным дифференциалом какого-либо выражения. Обобщённая сила  зависит от внешних параметров
зависит от внешних параметров  . Работа, произведённая над системой при изменении параметра
. Работа, произведённая над системой при изменении параметра 
 (2.2.6)
(2.2.6) , то получаем
, то получаем  . Так как
. Так как 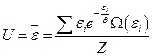 , то
, то  .
. .
. .
. и
и  . Поскольку энтропия
. Поскольку энтропия  есть функция состояния, то элементарное изменение этой величины
есть функция состояния, то элементарное изменение этой величины  заменяем дифференциалом
заменяем дифференциалом  .
. . Таким образом:
. Таким образом: (2.2.7)
(2.2.7) (2.2.8)
(2.2.8) (2.2.8)
(2.2.8) . Если внешний параметр – объём системы V, то
. Если внешний параметр – объём системы V, то (2.2.9)
(2.2.9) , для обратимых процессов
, для обратимых процессов  .
.


