
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термодинамические потенциалы.Содержание книги Поиск на нашем сайте
Величины удельной потенциальной энергии, кот обладает система в данном состоянии – термодинамические потенциалы. Термодинамическими потенциалами являются: U – внутр энергия, pV, TS, US. Пусть рабочее тело обладает внутр энергией dU и имеет температуру Т1, равную температуре окр среды, обладающей внутр энергией dU’. Общая энергия постоянна dU+dU’=0. Изменение энтропии: ds+dS’≥0. Если система совершит работу dW и передаст некоторое кол-во теплоты, то энтропия внешней среды увеличится на dS’. Тогда изменение энергии среды: dU’=TdS’+dW. Получим: dW≤dU’-TdS’. Величину U-TS обозначают F и называют свободной энергией системы. F=U-TS. Термодинамический потенциал Гельмгольца работа, которую может совершить рабочее тело в процессе при T=const, называется максимальной работой, которая равная уменьшению свободной энергии. dWmax=dF. Свободная энергия – та часть внутр энергии рабочего тела, кот может быть превращена в работу в процессе при постоянной температуре. Если наоборот, работа совершается над рабочим телом, то dV становится отрицательной, т.е. равна увеличению не всей, а только свободной внутр энергии за вычетом работы, кот превращается в теплоту. Т.е. внутр энергию можно разделить на 2 части. U=(U-TS)+TS; U=F+TS. Где F расходуется на внешнюю изотермическую работу, а TS в работе не участвует, поэтому ее называют связанной энергией или анергией. Для расширенной системы эта работа (dU+pV)-TS=H-TS=G. G – свободная энтальпия/ термодинамический потенциал Гиббса.
Все термодинамические потенциалы являются аддитивными величинами, т.е. их значение, например для смеси газов, равны сумме их значений для всех компонентов. Как и энтропия, для обратимых процессов все потенциалы неизменны, а для необратимых – уменьшаются.
Термодинамические процессы. Все возможные термодин процессы изменения состояния ид газа, в кот скорость движения газа пренебрежимо мало, могут быть описаны одним уравнением при допущении, что процессы обратимы и теплоемкость при их протекании постоянна. Изохорный процесс. При ус ловии dv=0; v=const (см рис). В реальных процессах теплоемкость меняется, однако это изменение близкое к 0, прямо пропорционально зависимости от температуры. Поэтому обычно при расчете процессов используют значение средней арифметической теплоемкости в данном процессе: Изобарный процесс. Dp=0; p=const; Изотермический процесс.
Адиабатный процесс. Происходит без теплообмена с окр средой. Политропный процесс.
Т.е. политропный процесс в зав-ти от n охватывает всю совокупность термомеханических процессов идеальных газов. Для понимания направления процесса, их делят на группы соответственно значениям n. (см рис). З группы политропных процессов: При
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.026 с.) |

 справедливо для изотермо-изобарных процессов. Полная максимальная работа за вычетом работы расширения равна изменению (уменьшению) свободной энтальпии (преобразование). См.рис.
справедливо для изотермо-изобарных процессов. Полная максимальная работа за вычетом работы расширения равна изменению (уменьшению) свободной энтальпии (преобразование). См.рис. – ур-е политропы.
– ур-е политропы.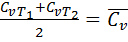 . Т.к. работа равна 0, то, в соответствии с 1м законом термодинамики, изменение внутр энергии равно кол-ву теплоты.
. Т.к. работа равна 0, то, в соответствии с 1м законом термодинамики, изменение внутр энергии равно кол-ву теплоты.  . Изменение энтропии
. Изменение энтропии  ;
; 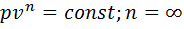
 (см.рис)
(см.рис) 

 . Т.к.
. Т.к.  , то изобара в TS координатах идет более полого, чем изохора.
, то изобара в TS координатах идет более полого, чем изохора.
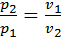 (см рис).
(см рис).  . Т.к. температура не меняется, то внутр энергия остается постоянной и, по 1-му закону термодинамики,
. Т.к. температура не меняется, то внутр энергия остается постоянной и, по 1-му закону термодинамики,  . При изотермическом сжатии работа, затраченная в этом процессе, происходит с отводом теплоты.
. При изотермическом сжатии работа, затраченная в этом процессе, происходит с отводом теплоты. 
 . (см рис).
. (см рис).  k – показатель адиабаты.
k – показатель адиабаты. 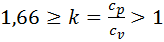 . Для одноатомного газа k=1,66; двухатомного k=1,4; трехатомного k=1,33.
. Для одноатомного газа k=1,66; двухатомного k=1,4; трехатомного k=1,33.  . Работа расширения, по 1 закону термодинамики, происходит за счет уменьшения внутр энергии.
. Работа расширения, по 1 закону термодинамики, происходит за счет уменьшения внутр энергии.  . Т.к.
. Т.к. 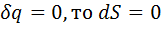 . А т.к.
. А т.к.  , то ПРОДОЛЖЕНИЕ 14 теплоемкость адиабатного процесса равна 0. Т.к. k>1, то изотерма идет более полого, чем адиабата.
, то ПРОДОЛЖЕНИЕ 14 теплоемкость адиабатного процесса равна 0. Т.к. k>1, то изотерма идет более полого, чем адиабата.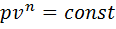

 ;
;  ;
;  ;
;  ;
;  ;
;  . Количество подведенной (отведенной) теплоты, по 1 закону, равно:
. Количество подведенной (отведенной) теплоты, по 1 закону, равно:  ;
;  ;
;  ;
;  ;
;  – теплоемкость в политропном процессе, а, т.к. n и k постоянны,
– теплоемкость в политропном процессе, а, т.к. n и k постоянны,  условно постоянна, то и
условно постоянна, то и 
 . Все процессы лежат между изохорой и изотермой. Расширение – с подводом теплоты, кот идет и на увеличение внутр энергии, и на совершение работы. С увеличением n доля теплоты, идущей на увеличение внутр энергии, уменьшается, а доля, идущая на совершение работы, увеличивается. Теплоемкость положительна.
. Все процессы лежат между изохорой и изотермой. Расширение – с подводом теплоты, кот идет и на увеличение внутр энергии, и на совершение работы. С увеличением n доля теплоты, идущей на увеличение внутр энергии, уменьшается, а доля, идущая на совершение работы, увеличивается. Теплоемкость положительна. . Графики располагаются между изотермой и адиабатой. Работа – за счет подводимой теплоты и уменьшения внутр энергии. С увеличением показателя n все большая часть работы, получается за счет уменьшения внутр энергии, и все меньшая – за счет подвода теплоты. Теплоемкость отрицательна.
. Графики располагаются между изотермой и адиабатой. Работа – за счет подводимой теплоты и уменьшения внутр энергии. С увеличением показателя n все большая часть работы, получается за счет уменьшения внутр энергии, и все меньшая – за счет подвода теплоты. Теплоемкость отрицательна. Графики располагаются между адиабатой и изохорой. При расширении газа процессы идут с уменьшением внутр энергии, с совершением работы и отводом теплоты. С увеличением n увеличивается доля теплоты, идущей на отвод … и уменьшается доля, идущая на совершение работы. Теплоемкость положительна. (см табл)
Графики располагаются между адиабатой и изохорой. При расширении газа процессы идут с уменьшением внутр энергии, с совершением работы и отводом теплоты. С увеличением n увеличивается доля теплоты, идущей на отвод … и уменьшается доля, идущая на совершение работы. Теплоемкость положительна. (см табл)


