Дифференциальное уравнение колебаний.
Похожие статьи вашей тематики
Свободные колебания. Рассмотрим колебания груза массы m, висящего на пружине, жесткость которой. Направим ось координат Х вертикально вниз, 
причем за начало отсчета примем точку О (рис.5.8), лежащую на одном уровне с центром масс m, когда груз неподвижен. При этом пружина растянута на величину x по сравнению с недеформированном состоянием. Величина упругой силы, действующей на массу m, равна kx. В положении равновесия
mg - kx = 0. (5-13)
Если теперь сместить груз из положения равновесия, то он начнет совершать колебательное движение. Колебания, которые происходят в системе, выведенной из положения равновесия и затем предоставленной самой себе, называются свободными или собственными колебаниями, а частота, с которой происходят эти колебания, называется собственной частотой. Пусть в некоторый момент времени смещение груза равно х. Тогда второй закон Ньютона в проекции на ось Х может быть записан в следующем виде:
max = mg - k (x +x) или с учетом (5-13)
max = - kx. (5-14)
В свою очередь, уравнение (5-14) можно записать иначе, если представить ускорение тела через вторую производную смещения по времени ax = d2x/dt 2 и обозначить величину k/m = 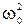 : :
 = - = - 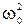 x. (5-15) x. (5-15)
Уравнение (5-15) является дифференциальным уравнением второго порядка, однако его решение можно просто угадать простым перебором всех элементарных функций, из которых только функции синуса и косинуса удовлетворяют решению этого уравнения. Действительно, если
смещение x = A sin(w0t + j), (5-16)
то скорость тела  , (5-17) , (5-17)
и ускорение тела 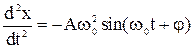 . (5-18) . (5-18)
Сравнение (5-16) и (5-18) показывает, что действительно (5-16) является решением уравнения (5-15). Величины А и j остаются произвольными, для их определения необходимо использовать начальные условия, т.е. значения смещения и скорости тела в начальный момент времени. Например, если при t = 0 x (0)= 0, а v(0) = v0, то из (5-16) следует, что sinj = 0 и j = 0, a из (5-17) величина А = v0/w0. При этих условиях решением уравнения (5-15) служит функция х(t) =  . Задание тех или иных начальных условий обычно определяется конкретными условиями поставленной задачи. . Задание тех или иных начальных условий обычно определяется конкретными условиями поставленной задачи.
Затухающие колебания. В реальной жизни любой колебательный процесс постепенно затухает из-за наличия сил трения. Для колебаний груза на пружине существенную роль играет так называемое вязкое трение, сила которого при малых смещениях оказывается пропорциональной величине скорости тела:
Fтрен = - bv = - b  . (5-19) . (5-19)
В этом случае второй закон Ньютона (уравнение движения) для груза, колеблющегося на пружине, приобретает такой вид:
  + mg - k (x +x). (5-20) + mg - k (x +x). (5-20)
Вводя обозначения  , это уравнение можно преобразовать так: , это уравнение можно преобразовать так:
 , (5-21) , (5-21)
где по-прежнему  . Решение этого дифференциального уравнения может быть получено обычным способом, но можно показать, что уравнение (5-21) можно свести к уравнению типа (5-15). Для этого достаточно ввести замену переменных x(t) = z (t)e - bt. Проводя операцию дифференцирования, имеем: . Решение этого дифференциального уравнения может быть получено обычным способом, но можно показать, что уравнение (5-21) можно свести к уравнению типа (5-15). Для этого достаточно ввести замену переменных x(t) = z (t)e - bt. Проводя операцию дифференцирования, имеем:
 ; 2b ; 2b  ; ;
 , ,  . .
С учетом этого уравнение (5-21) может быть записано в таком виде:
 + +  + +  = 0 = 0
После сокращения на величину  и приведения подобных членов получаем: и приведения подобных членов получаем:
 . (5-22) . (5-22)
Сравнивая полученное уравнение с выражением (5-15), нетрудно заметить их почти полную идентичность; различие состоит лишь в том, что частота колебаний в (5-22) определяется из формулы  . Таким образом решение уравнения (5-21) имеет вид: . Таким образом решение уравнения (5-21) имеет вид:
 , (5-23) , (5-23)
где как и ранее величины А и j определяются из начальных условий. В большинстве случаев b<<w0 и w3» w0. Решение (5-23) представляет уже негармоническое колебание, т.к. его амплитуда А  уменьшается с течением времени. Относительное изменение амплитуды за период колебания характеризуется декрементом затухания D, величина которого находится из выражения: уменьшается с течением времени. Относительное изменение амплитуды за период колебания характеризуется декрементом затухания D, величина которого находится из выражения:
 , (5-24) , (5-24)
т.е. декремент затухания равен относительному уменьшению амплитуды за время, равное периоду колебания. Натуральный логарифм D называют логарифмическим декрементом затухания d, т.е. d = ln D = bТ.
|