
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення довжини світлової хвилі за допомогою біпризми Френеля.Содержание книги
Поиск на нашем сайте
Прилади і матеріали: оптична лава, рейтери, лазер, біпризма Френеля, короткофокусна лінза, щілина, екран.
ТЕОРЕТИЧНІ ВІДОМОСТІ. Накладання світлових хвиль, в результаті якого в одних точках виникають коливання з максимальною амплітудою, а в інших - з мінімальною, називається інтерференцією світла. Для одержання інтерференції необхідно, щоб світлові хвилі, які випромінюються джерелом, були когерентними, тобто щоб коливання від них мали сталу різницю фаз. Когерентні хвилі можна одержати за допомогою біпризми Френеля. Хід променів в біпризмі показаний на Мал.1.
Мал.1. Біпризма ABС являє собою оптичну систему з двох призм з малими кутами заломлення З інтерференційної картини можна визначити довжину світлової хвилі:
де r - відстань від щілини до біпризми (див. мал.2); d - відcтань від щілини до лінзи; B - стала біпризми; DC – ширина інтерференційної смуги. Звичайно На екрані спостерігається k смуг, які мають загальну ширину l. Тоді:
Якщо відстань лінза - екран, при якій спостерігається картина, дорівнює а, то при оптичній силі D формулу (1) можна записати:
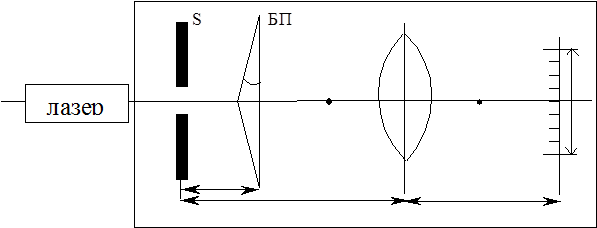
ОПИС УСТАНОВКИ. Установка складається з оптичної лави, на якій послідовно розміщені лазер, щілина, біпризма, лінза, екран (Мал.2). Всі вони юстовані відносно однієї оптичної осі (якою є промінь лазера).
Мал.2. Біпризма (БП) виготовлена з скла, показник заломлення якого n= 1,85 і має заломлюючий кут α =15' або 4,36·10-3 рад. В розрахунках використовується біпризма, постійна якої B рівна
Лінза (Л2) має фокусну віддаль ~3 см і оптичну силу D= 33 діоптрії. Лінза встановлена так, щоб інтерференційна картина від двох пучків, заломлених біпризмою, утворилась безпосередньо перед переднім фокусом лінзи. Це дозволяє спостерігати на екрані (Е) збільшену інтерференційну картину.
ПОРЯДОК РОБОТИ. 1. Встановити прилади згідно Мал. 2. УВАГА: лазер вмикає викладач (лаборант) після перевірки схеми. 2. Відрегулювати ширину щілини і її розміщення відносно променя лазера так, щоб отримати на екрані картину смуг загальною шириною близько 2 см. 3. Виміряти віддалі r, d, a, l і кількість смуг k. 4. Результати занести в таблицю. 5. Пункти 2 і 3 повторити не менше 5 разів. 6. По формулі (2) обчислити довжину хвилі для кожного досліду. Результати занести в таблицю.
1. Обчислити похибку вимірювань.
λсер = (796 ± 71) нм. (tα = 4.3, α = 95%)
КОНТРОЛЬНІ ЗАПИТАННЯ. 1. В чому полягає явище інтерференції? 2. Чому не спостерігається інтерференція від двох незалежних джерел світла? 3. Назвіть методи одержання когерентних світлових хвиль. 4. Накресліть хід променів в біпризмі Френеля. 5. Запишіть умови виникнення максимумів і мінімумів інтерференції. 6. Поясніть, що таке просторова та часова когерентність. 7. Які методи спостереження інтерференції Ви знаєте?
Лабораторна робота № 8. Визначення показника заломлення рідких речовин З допомогою інтерферометра Релея.
Прилади і матеріали: інтерферометр Релея, дистильована вода, розчин спирту (5% і 10%).
ТЕОРЕТИЧНІ ВІДОМОСТІ. В інтерферометрі Релея використовується дифракція Фраунгофера на двох щілинах (мал.1). розрахунок інтенсивності світлових коливань після проходження двох щілин можна зробити, використавши принцип Гюйгенса-Френеля.
Мал.1. Інтенсивність світлових коливань на екрані записується виразом:
де І0- інтенсивність світла в центрі дифракційної картини від однієї щілини; k - хвильовий вектор, Перший множник в (1) дає інтенсивність при дифракції на одній щілині шириною b, а другий - інтерференцію хвиль на двох щілинах, розташованих на відстані d. Розподіл інтенсивності на екрані для цього випадку приведений на мал..2 (пунктирна лінія – дифракційна картина від однієї щілини).
Мал.2. Практичний інтерес мають яскраві інтерференційні смуги, розташовані в межах центрального дифракційного максимуму, тобто в області Число смуг в цій області (головних максимумів) залежить від відстані між щілинами d. Очевидно, чим більше d, тим більше число смуг спостерігається в згаданому інтервалі. Мал.2 відповідає інтерференційній картині в монохроматичному світлі. Якщо щілини освітлюються білим світлом, то всі смуги, крім центральної, будуть забарвленими. Таким чином, центр інтерференційної картини візуально визначається як біла смуга, обмежена чорними мінімумами.
КОНСТРУКЦІЯ ІНТЕРФЕРОМЕТРА. Інтерферометр складається з коліматора (щілина S і об‘єктив О1) подвійної щілини Д та зорової труби (об‘єктив О2 ,окуляр О). Щілина S освітлюється лампою розжарення Л через конденсор К. Ця щілина розташована в фокусі об‘єктива О1. Світло, що проходить, через цей об‘єктив, падає на подвійну щілину Д паралельним пучком (плоска хвиля), що забезпечує виконання умов дифракції Фраунгофера при невеликих розмірах установки. Дифракційна картина отримується в фокальній площині об‘єктива О2 і розглядається через окуляр О. Кожному значенню дифракційного кута j в фокальній площині об‘єктива О2 відповідає лінія, що паралельна щілинам, яка відстоїть від оптичної вісі на відстані
де f – фокусна відстань об‘єктива О2. Відстань між інтерференційними смугами
Звичайно f= 50 см., d= 1 cм., тобто
Мал.3. Інтерферометр Релея може застосовуватись для визначення невеликих змін показників заломлення рідин і газів, визначення домішок різних газів в повітрі (зокрема для вимірювання концентрації рудничних газів в шахтах). Суть методу полягає в тому, що на шляху світлових хвиль розміщується два прозорих об‘єкта, наприклад, дві кювети з різними рідинами (мал.3). Це приводить до появи різниці ходу між променями В ІТР-1 для зміщення інтерференційної картини в горизонтальній площині використовується компенсатор Жамена, що складається з двох однакових плоско-паралельних пластин. Нахилом однієї з них можна одержати додаткову різницю ходу В окулярі ІТР-1 видно не одну, а дві системи інтерференційних смуг. Верхня система смуг рухома. Вона утворюється при інтерференції променів, які пройшли під кюветою і компенсатором. Для роздільного спостереження двох систем в окулярі застосована не сферична, а циліндрична оптика.
ПОРЯДОК РОБОТИ.
1. Вивчити інструкцію до приладу ІТР-1. 2. Ввімкнути освітлювач інтерферометра і впевнитись, що в полі зору спостерігаються дві системи смуг інтерференційної картини. 3. Перед початком вимірювань слід прокалібрувати компенсатор та встановити початок відліку. Для цього кювети 2-3 рази промивають дистильованою водою, встановлюють їх в інтерферометр та помічають поділки барабана компенсатора (мікрометричного гвинта). Суміщення проводять по центральній (нульовій) смузі. Цей відлік мікрометричного гвинта N0 є початком відліку для подальших вимірювань (0 кювети). Для градуювання компенсатора послідовно суміщають першу, другу і т.д. рухомі смуги з центральною (білою) смугою нижньої опорної картини і записують відповідні покази мікрометра. По цим даним визначають середнє число поділок, що приходяться на зміщення на одну лінію N1.
Повітря: N0 = 0.9 мкм, N1 = 0.54 мкм, N2 = 0.24 мкм, n1 = n2 = nсер = 0.33 мкм/лінію.
4. Влити воду в ліву кювету “Л” і розчин спирту в праву (ближчу до вас) кювету “П”. Поставте кювети в інтерферометр і проведіть виміри зміщення картини N від нуля до нового положення інтерференційної картини, тобто N-N0.
Спирт: N0 = 11.25 мкм, N1 = 10.85 мкм, N2 = 10.45 мкм. n1 = n2 = nсер = 0.4 Вода – вода: N0 = 0.9 мкм, N1 = 1.15 мкм, N2 = 0.57 мкм, N3 = 0.29 мкм. n1 = n2 = n3 = nсер = 0.29
5. Провести виміри декілька разів. Результати занести в таблицю. Визначити на скільки ліній змістилась інтерференційна картина. Зміщення в лініях:
Для «вода-спирт»: 1h1 = 2Для «повітря-спирт». 3h2 = 1. Вважаючи воду еталонною рідиною з відомим показником заломлення n0, визначити показник розчину спирту по формулі:
n1 = 1.33299 + n2 = 1.33299 + nсер = 1.37269 де
7. Обчислити похибку вимірювань, результат дати у вигляді:
1 2tα = 4.3, α = 95%. 4n = 1.4 ± 0.2, α = 95% 7. Додаткове завдання: спостерігати дифракцію Фраунгофера на одній щілині (без кювети), по черзі закриваючи щілини в діафрагмі (мал.3). Занотуйте свої спостереження відносно положення дифракційних смуг і дайте відповідні пояснення.
КОНТРОЛЬНІ ЗАПИТАННЯ.
1. Чому інтерференційні максимуми в ІТР-1 забарвлені? 2. Чому в ІТР-1 не використовується монохроматичне світло? 3. Поясніть принцип роботи інтерферометра. 4. Яке призначення компенсатора? 5. Який вигляд має інтерференційна картина від двох щілин, як вона змінюється при зміні ширини щілини і відстані між ними? 6. Який фізичний зміст має показник заломлення? Якою характеристикою молекул речовини він визначається?
ЛАБОРАТОРНА РОБОТА № 9
ВИВЧЕННЯ ПРОСТОРОВОЇ КОГЕРЕНТНОСТІ ПО СХЕМІ ЮНГА.
Прилади: лазер, оптична лава, рейтери, подвійна щілина, екран, короткофокусна лінза.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Когерентність хвиль є необхідною умовою одержання стійкої інтерференційної картини. Когерентність - це узгодженість в часі і просторі декількох хвильових процесів. Будь-який коливний процес має такі характеристики: амплітуда А, період Т, циклічна частота w, початкова фаза j0. Коливання називається монохроматичним (або гармонічним), якщо воно описується виразом: y = A cos(wt + j0) (1) при цьому частота w, амплітуда А, і початкова j0 постійні в просторі і часі. Поширення такого коливання в просторі вздовж напрямку ОХ являє собою плоску монохроматичну хвилю у = А соs(wt-kx+j0) (2) де k=2p/l - хвильовий вектор. Дві світлові хвилі будуть когерентними, якщо різниця їх фаз не змінюється з часом. Суперпозиція когерентних хвиль приводить до появи інтерференційної картини. Практичні способи одержання когерентних світлових хвиль такі, що їх початкові фази виявляються рівними. Умова когерентності забезпечується лише для хвиль однакової частоти w. Для спостереження чіткої інтерференційної картини необхідно також, щоб хвилі були поляризовані в одній площині і мали приблизно рівні амплітуди А. Для кількісної оцінки когерентності хвиль вводиться два поняття: часова і просторова когерентність хвиль. Ці поняття вводять для слабко когерентних хвиль, різниця фаз яких змінюється повільно можливо за рахунок зміни частоти w, або за рахунок зміни початкової фази j0. Якщо за час t фаза хвилі змінюється на p, то t називається часом когерентності. За t в інтерференційній картині максимум зміниться на мінімум, а хвилі проходять відстань L= L-довжина когерентності. Час когерентності одиночних атомів 10-8с, у розігрітогo твердого тіла - 10-15с, у лазера - 10-5с. Поняття просторової когерентності вводиться для опису властивостей хвилі в площині, перпендикулярній до напрямку її поширення. Наприклад, якщо є два когерентні джерела світла, розміри і взаємне розміщення яких дозволяє спостерігати інтерференцію, то вони називаються просторово-когерентними. Просторова когерентність буде мати місце у цих двох джерел до того часу, поки різниця їх ходу не перебільшить величину L= З цієї причини спостерігати інтерференцію в променях звичайних джерел світла (свічка, електролампа, Сонце і т.п.) дуже важко, бо при різниці ходу більше 10-6м, (порядку довжини хвилі) просторова когерентність зникає і інтерференція не спостерігається Перше спостереження інтерференції з сонячним світлом провів в 1807 році англійський вчений Томас Юнг. Схема установки цього досліду наведена на мал.1.Сонячне світло попадало в темне приміщення через вузьку щілину S від якої світлова хвиля падала на дві рівновіддалені від осі паралельні щілини S1 S2. Таким чином, щілини S1,S2 виконували роль когерентних джерел. Інтерференція спостерігалась на екрані Е, який розміщений на віддалі l паралельно S1S2..При відстані між щілинами d різниця ходу хвиль Dr для деякої точки екрана, віддаленої від оптичної осі на відстані x, може бути знайдена так:.
Відомо, що при різниці ходу: Dr=r1-r2= де m=0,1,2,…буде спостерігатись в точці x на екрані світла смуга. Тому координати світлих смуг будуть: x=ml
де l довжина хвилі випромінювання. Відстань між двома темними смугами, яка називається шириною інтерференційної смуги, дорівнює: Dx=ll/d (6) Величина Dx не залежить від порядку інтерференції, співпадає з відстанню між світлими смугами і є постійною для даних l,d,l. Інтерференційна картина складається з темних і світлих смуг однакової ширини, що чергуються. З природним світлом можна отримати лише кілька смуг слабої інтенсивності, дослідити які дуже важко. Це пояснюється його низькою просторовою і часовою когерентністю. Якщо джерелом світла використовується лазер, то можна легко отримати інтерференційну картину із декількох десятків яскравих смуг, що і досягається в цій роботі.
ОПИС УСТАНОВКИ.
В даній роботі використовується гелій-неоновий лазер. Короткофокусна лінза Л2 і подвійна щілина встановлені за допомогою рейтерів на оптичній лаві, екран Е розміщується на відстані від щілини більше 1,5м.
ПОРЯДОК РОБОТИ
1 Встановити всі прилади на оптичну лаву згідно Мал.2. 2. Ввімкнути лазер і відрегулювати лінзу і лазер так, щоб промінь від лінзи попав на подвійну щілину S1,S2, при цьому на екрані повинна спостерігатись симетрична відносно центра картина з декількох десятків смуг. 3. Виміряти відстань щілина -екран, результати занести в таблицю.
4. Виміряти загальну ширину щілини декількох світлих смуг (k) на екрані. Результати занести в таблицю. 5. З формули (6) обчислити довжину хвилі l= λ1 = λ2 = λ3 = λ4 = λ5 =
6. Пункти 3, 4, 5, повторити не менше 5 разів для різних значень l, k. 7. Обчислити середнє значення lс та похибку вимірювання.
λс = 652.2 нм
8. Записати кінцевий результат l=lс±Dl(м) і зробити висновок. λ = (0.65 ± 0.02) * 10-6 м, α = 95%.
КОНТРОЛЬНІ ЗАПИТАННЯ
1. Дайте визначення просторової і часової когерентності. 2. Які хвилі називають когерентними? 3. Вивести формули (5), (6). 4. Які відомі способи спостереження двопроменевої та багатопроменевої інтерференції? 5. Які обмеження для порядку інтерференції m?
S S1 S2 l E O r1 r2 x
Мал.1
Л2 Е О! D S1S2 l > 1,5 лазер О
Мал.2
ЛАБОРАТОРНА РОБОТА № 10 ВИВЧЕННЯ ДИФРАКЦІЙНОЇ РЕШІТКИ ЗА ДОПОМОГОЮ ГОНІОМЕТРА
Прилади і матеріали: гоніометр ГМ5, дифракційна решітка, ртутна лампа, джерело живлення лампи.
ТЕОРЕТИЧНІ ВІДОМОСТІ
φ b d a a) Дифракційна решітка - це пристрій, що має N однакових паралельних щілин на рівних відстанях одна від одної. Здебільшого дифракційна решітка може бути у вигляді плоскої скляної поверхні, на якій спеціальною машиною нанесено досить багато (інколи сотні тисяч) прямих рівновіддалених штрихів. На таких решітках спостереження можна вести в світлі, що проходить і у відбитому світлі. Переріз плоскої решітки має вигляд, що показаний на мал.1, де a - ширина штриха, b - ширина щілини, d=a+b - стала, або період дифракційної решітки, d= б) Мал.1 Якщо на решітку нормально до її площини падає плоска монохроматична хвиля довжиною l, то на кожній з щілин b відбувається дифракція світла і кожна щілина стає джерелом циліндричної хвилі. Оскільки стала решітки досить мала (0,01мм), то хвилі, що йдуть від сусідніх щілин будуть когерентні і можуть інтерферувати. Розрахунок інтерференції світла від усіх N щілин дифракційної решітки дає вираз для інтенсивності світла, що поширюється під кутом j до нормалі:
Ij=I0 де u= Графік функції Ij(sinj) має вигляд, що даний на мал.2. Подібна дифракційна картина спостерігається у фокальній площині лінзи, яку розташовують за дифракційною решіткою.
I j 0 sin j
Мал.2 Пунктирна обвідна відповідає розподілу інтенсивності при дифракції на одній щілині, помноженій на N2(Ilj b×sinj=±m×l (2) де m=1,2….. визначає порядок мінімуму. Аналізуючи вираз (1) можна також показати, що головні максимуми спостерігаються під кутами дифракції j, які задовольняють умові: d×sinj=±m×l (3), де m=!, 2,…і визначає порядок максимуму. Ці максимуми є результатом інтерференції світла від сусідніх щілин. Якщо в результаті такої інтерференції хвилі гасять одна одну, то виникають додаткові мінімуми між сусідніми головними максимумами, їх число дорівнює (N-1) і умовою додаткового мінімуму є d×sinj= де R=1, 2, …, N-1 Картина, що показана на Мал.2 спостерігається в монохроматичному світлі. Якщо дифракційну решітку освітлювати білим світлом, то побачимо картину, що є результатом накладання таких картин для різних довжин хвилі. Замість вузьких максимумів 1, 2, …порядків (при sinj= Як бачимо, дифракційна решітка є спектральним приладом і характеризується роздільною здатністю R та кутовою дисперсією D. Найменша різниця довжин хвиль двох спектральних ліній dl, при яких спектральний прилад розділяє їх окремо, називається спектральною роздільною відстанню, а величина R= Спектральні лінії вважаються розділеними (за критерієм Релея), коли головний максимум лінії збігається з першим додатковим мінімумом того ж порядку для другої довжини хвилі (Мал.3). Це означає, що
d×sinj=m×(l+dl) d×sinj=(m+ тоді dl=l¢-l= R=
l+dl l Мал.3 Як видно, роздільна здатність решітки залежить від загальної кількості її штрихів і зростає з порядком спектру. Кутовою дисперсією називається величина
D=
де dj кутова відстань між двома спектральними лініями, яким відповідають довжини хвиль li=l+dl.. Для визначення D продиференціюємо формулу (3), тоді d×cosj×dj=m×dl, звідки
D= Для малих кутів дифракції j маємо cos j»1;
D= де L - довжина робочої ділянки решітки. Дисперсія решітки визначається її сталою d і зростає з порядком хвилі, тобто дифракційний спектр рівномірний для всіх довжин хвиль, в цьому його перевага перед спектром, одержаним від призми, який розтягнутий у фіолетовій, стиснутий у червоній частини спектру.
ОПИС ПРИЛАДУ.
Гоніометр ГМ5 - це оптичний контрольно-вимірювальний прилад лабораторного типу, призначений для технічних вимірювань 1 2 3 4 14 9 6 5 7
кутів між полірованими гранями твердих прозорих і непрозорих тіл, пірамідальності призм. Діапазон вимірювання кутів - 0…3600 з точністю до 0,5". Загальний вигляд гоніометра показаний на Мал.4.
Мал.4 Гоніометр складається з автоколіматора 1, маховичка 2 фокусування автоколіматора, навідного гвинта 3, кришки об’єктива 4, столика 5, гвинтів нахилу 6 та повороту столика 7, відлікового мікроскопа 8, окуляра 9, маховичка відлікового мікроскопа 10, корпуса 11.З допомогою гвинтів 12 здійснюється суміщення спектральних ліній з початком відліку. До об’єктива гоніометра 13 із вхідною щілиною, ширина якої регулюється мікрометричним гвинтом 14, приставляють ртутну лампу в захисному кожусі. Вмикання гоніометра в мережу220 В відбувається тумблером "СЕТЬ" 15. Ртутна лампа вмикається від блоку живлення. Відлік кутів проводять за допомогою відлікового мікроскопа 9, в полі зору якого спостерігають дві шкали (Мал.6).
ПОРЯДОК РОБОТИ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.243 (0.01 с.) |

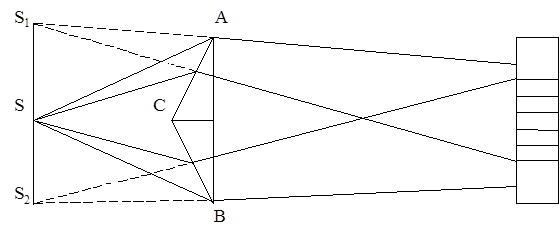
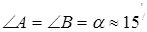 , які з’єднані своїми основами. Якщо промені від щілини S, що забезпечує просторову когерентність пучка світла і паралельна ребру С, падають на біпризму Френеля, то внаслідок заломлення вони розділяються на два пучки, що перетинаються за призмою. Продовження заломлених променів перетинаються в точках S1 і S2, які є уявними зображеннями щілини S і можуть розглядатись як когерентні джерела світла. В області накладання заломлених світлових хвиль можна спостерігати інтерференційну картину в вигляді темних і світлих смуг, що чергуються. Максимум нульового порядку інтерференції знаходиться на оптичній вісі системи, яка проходить через щілину S та ребро С біпризми.
, які з’єднані своїми основами. Якщо промені від щілини S, що забезпечує просторову когерентність пучка світла і паралельна ребру С, падають на біпризму Френеля, то внаслідок заломлення вони розділяються на два пучки, що перетинаються за призмою. Продовження заломлених променів перетинаються в точках S1 і S2, які є уявними зображеннями щілини S і можуть розглядатись як когерентні джерела світла. В області накладання заломлених світлових хвиль можна спостерігати інтерференційну картину в вигляді темних і світлих смуг, що чергуються. Максимум нульового порядку інтерференції знаходиться на оптичній вісі системи, яка проходить через щілину S та ребро С біпризми. (1),
(1),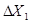 мала і для її спостереження використовують лінзу, одержуючи збільшене зображення на екрані.
мала і для її спостереження використовують лінзу, одержуючи збільшене зображення на екрані.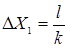
 (2)
(2)

 = 0.089
= 0.089
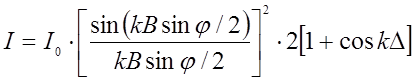 (1),
(1), різниця ходу променів від двох щілин.
різниця ходу променів від двох щілин.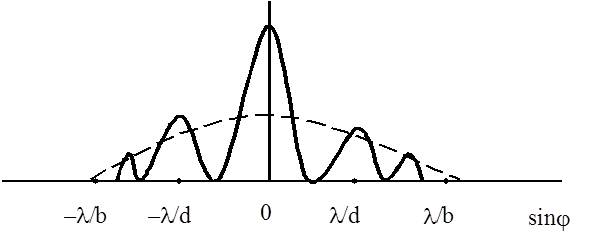
 | sin φ|
| sin φ|  / b.
/ b.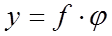 ,
, в фокальній площині рівна:
в фокальній площині рівна: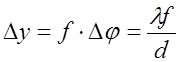 (2)
(2)
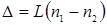 , де L – товщина шару рідини, n1 і n2 – показники заломлення двох рідин. Внаслідок інтерференції променів з різницею ходу
, де L – товщина шару рідини, n1 і n2 – показники заломлення двох рідин. Внаслідок інтерференції променів з різницею ходу 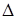 інтерференційна картина зміщується в горизонтальній площині відносно оптичної системи приладу.
інтерференційна картина зміщується в горизонтальній площині відносно оптичної системи приладу.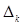 . При
. При 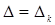
 , k – кількість ліній, на яку відбулося зміщення.
, k – кількість ліній, на яку відбулося зміщення. 0.3 мкм/лінію.
0.3 мкм/лінію.





 .
.

 ,
,

 - довжина хвилі джерела світла (для білого світла можна користуватись
- довжина хвилі джерела світла (для білого світла можна користуватись  E%
E% 0.0235*4.3 = 0.101
0.0235*4.3 = 0.101 , де
, де =l2+(x+d/2)2,
=l2+(x+d/2)2,  =l2+(x-d/2)2 (3)
=l2+(x-d/2)2 (3) (4)
(4) (5)
(5) (d=1,4×10-4м), де Dх=
(d=1,4×10-4м), де Dх=  .
.





 , де n - кількість штрихів на одиницю довжини решітки, j - кут дифракції.
, де n - кількість штрихів на одиницю довжини решітки, j - кут дифракції. (1)
(1) .sinj,
.sinj,  .sinj, I0 - інтенсивність світла, що проходить через одну щілину, коли j=0 Формула (1) - основна в теорії дифракційної решітки. Перший множник характеризує розподіл інтенсивності при дифракції плоскої хвилі на кожній щілині, а другий враховує інтерференцію між пучками, що дифрагують під кутом j від N щілин.
.sinj, I0 - інтенсивність світла, що проходить через одну щілину, коли j=0 Формула (1) - основна в теорії дифракційної решітки. Перший множник характеризує розподіл інтенсивності при дифракції плоскої хвилі на кожній щілині, а другий враховує інтерференцію між пучками, що дифрагують під кутом j від N щілин.


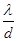


 N2). Тому положення головних мінімумів знаходять з умови мінімумів на одній щілині.
N2). Тому положення головних мінімумів знаходять з умови мінімумів на одній щілині. ×l (4)
×l (4) ;…) побачимо спектри відповідно першого, другого та ін. порядків. Максимум нульового порядку (sinj=o) буде білого кольору, тому що тут накладаються максимуми для всіх довжин хвиль.
;…) побачимо спектри відповідно першого, другого та ін. порядків. Максимум нульового порядку (sinj=o) буде білого кольору, тому що тут накладаються максимуми для всіх довжин хвиль. - роздільною здатністю приладу. (5)
- роздільною здатністю приладу. (5) )×l
)×l ×l=m×(l+dl)
×l=m×(l+dl) , звідки
, звідки (6)
(6) (7),
(7), (8)
(8) (9)
(9)


