Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення показника заломлення скла за допомогою лазера.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лабораторна робота № 1 Визначення показника заломлення скла за допомогою лазера.
Прилади: оптична лава, лазер, рейтери, короткофокусна лінза, екран, плоско-паралельна скляна пластина.
ТЕОРЕТИЧНІ ВІДОМОСТІ. Відомо, що промінь світла на межі двох середовищ заломлюється. Виключення складає випадок, коли промінь падає на межу поділу нормально. В цьому випадку промінь не змінює свого напрямку. На мал. 1 показано хід променя, що падає на плоско-паралельну пластинку під кутом a. Якщо грані S і S¢ пластинки плоско-паралельні, то промінь АО¢ буде паралельним вісі ОО, тобто початковому напрямку. Зміщення променя в пластинці h = АС. Величина h залежить від товщини d пластинки, показників заломлення скла і середовища, в якому ця пластинка знаходиться, а також від кута падіння a. Знайдемо цю залежність з мал. 1: зD ОАС: h = ОА sin (a -b), (1) ОА= d/ cos b, (2) H = d sin (a - b)/ cos b (3) З закону заломлення для випадку скляної пластинки в повітрі можна записати: де n – показник заломлення скла.
Мал.1. Із (3) і (4) можна одержати формулу для визначення показника заломлення скла:
В пластинах з товщиною d декілька сантиметрів зміщення буде порядку декількох міліметрів. Для кращого спостереження величини h бажано застосувати короткофокусну лінзу. Хід променів в такому випадку показаний на мал.2.
Мал. 2 На екрані Е2 отримаємо збільшене зміщення променя Н, яке зв’язане з h виразом:
де D – оптична сила лінзи, b – віддаль лінза-екран. Враховуючи (6) можна записати (5) у вигляді:
Остання формула дозволяє визначити показник заломлення скла при відомих значеннях a, d, H.
ОПИС УСТАНОВКИ На оптичній лаві, на одній оптичній осі розміщується лазер, екран з діафрагмою (Е1), плоско-паралельна пластинка (ПП), лінза (Л) і екран (Е2). Діафрагма в Е1 служить для звуження променя лазера. Пластина ПП закріплена на юстовочному столику, який може повертатись і має лімб для відліку кутів повороту, Екран Е2 розташований на віддалі b від лінзи. В даній роботі використовується лінза з фокусною віддаллю F= 0,11 м (D= 9 діоптрій) і скляна пластина товщиною 0,02 м. На Мал. 3 наведена схема установки.
Мал.3.
ПОРЯДОК ВИКОНАННЯ РОБОТИ 1. Розташувати на оптичні лаві всі прилади згідно
2. Промінь лазера направити в діафрагму екрану Е2 регулюючими гвинтами лазера. 3. Виставити лінзу на одній оптичній вісі з променем лазера. Для цього зняти разом з рейтером плоско-паралельну пластинку ПП, так, щоб промінь лазера попадав на лінзу. Відрегулювати лінзу так, щоб промінь попадав строго в центр і, відбиваючись від її передньої поверхні, падав назад в отвір діафрагми (цей промінь більш яскравий із відбитих променів). 4. Ставимо рейтер з пластинкою ПП на оптичну лаву. Пластинку ПП з допомогою гвинтів ставимо так, щоб промінь лазера падав на неї нормально. При нормальному падінні відбитий від пластинки промінь йде в отвір діафрагми. 5. Відмітити положення лімбу столика a0 і на екрані положення променя лазера H0. Результати занести в таблицю. 6. Обертаючи гвинт, повернути пластинку на кут a, вказаний в п.1 таблиці. 7. Відмітити на екрані Е2 нове положення променя лазера H1¢ і обчислити його зміщення на екрані H1=H1¢ – H0. 8. Пункти 4, 5, 6, 7 проробити для всіх значень a, вказаних в таблиці. 9. Виміряти відстань b від лінзи до екрана Е2. 10. По формулі (7) обчислити значення n для кожного a. 11. Знайти середнє значення показника заломлення скла n та обчислити похибку вимірювань.
Таблиця
КОНТРОЛЬНІ ЗАПИТАННЯ. 1. Сформулюйте закони заломлення світла. 2. Що називається показником заломлення світла, його зв’язок з характеристиками діелектрика. 3. Вивести формули (5), (6), (7). 4. Побудувати хід променів в плоскопаралельних пластинках, середовищах. 5. Показати зміщення променя в пластинці та знайти його величину.
Лабораторна робота № 2. Визначення показника заломлення скла з допомогою Мікроскопа.
Прилади і матеріали: вимірювальний мікроскоп з мікрометричним гвинтом, мікрометр, скляна пластинка з штрихами на обох поверхнях.
ТЕОРЕТИЧНІ ВІДОМОСТІ. При проходженні світла через плоску межу двох прозорих речовин неоднакової оптичної густини, падаючий промінь розділяється на два промені – відбитий ОВ і заломлений OD.(мал.1.)
Напрям цих променів визначають закони відбивання і заломлення світла: Промінь падаючий і відбитий лежать в одній площині з нормаллю до поверхні в точці падіння і кут відбивання чисельно дорівнює куту падіння.
Мал.1. Промінь падаючий і заломлений лежать в одній площині з нормаллю до поверхні в точці падіння і відношення синуса кута падіння і до синуса кута заломлення дорівнює відношенню швидкості світла в першому середовищі v 1 до швидкості світла в другому середовищі v 2:
Явище заломлення світла говорить про те, що світло поширюється в різних середовищах з різною швидкістю. Для двох даних середовищ відношення швидкості світла в середовищі 1 до швидкості світла в середовищі 2 – є величина стала і називається відносним показником заломлення другого середовища відносно першого. Якщо середовище 1 – вакуум, то показник заломлення n даного середовища 2 по відношенню до вакууму називається абсолютним показником заломлення даного середовища або просто показником (коефіцієнтом) заломлення. Абсолютний показник заломлення середовища
де c – швидкість світла в вакуумі; Показник заломлення залежить від довжини хвилі світла і від властивостей середовища. Абсолютні показники заломлення в області прозорості речовини більші одиниці. Це означає, що швидкість поширення світла в даному середовищі завжди менша, ніж у вакуумі. Відносний показник заломлення двох середовищ n21 пов‘язаний з абсолютним показником заломлення середовищ n1 і n2 відношенням:
Для визначення показників заломлення речовини існують різні методи. Одним з них є метод визначення показника заломлення за допомогою мікроскопу. основі методу лежить явище уявного зменшення товщини скляної пластинки внаслідок заломлення світлових променів, які проходять в склі при розгляданні пластинки нормально до її поверхні. Схема проходження променів показана на Мал.2.
Мал.2. З точки А, яка знаходиться на нижній поверхні скляної пластинки виходять два промені світла 1 і 2. Промінь 2 падає на пластинку нормально до її поверхні і тому не зазнає заломлення. Промінь 1 падає під кутом і заломлюється виходячи з пластинки в точці О по напрямку до точки Д. При виході із пластинки промінь ОД утворює кут заломлення r – більший, ніж кут падіння. Якщо дивитись на пластинку зверху, то спостерігач буде бачити точку перетину променів ОД і АС не в точці А, а в точці Е, тобто видима товщина пластинки СЕ = а менша дійсної її товщини СА= h. Для променів, близьких до нормалі, кути падіння і заломлення малі. В цьому випадку синуси кутів можна замінити на тангенси і по закону заломлення світла написати (розглядаючи зворотний хід променів, тобто від Д до А):
З мал.2 видно, що тоді одержимо: Значить, показник заломлення скла можна знайти як відношення дійсної товщини пластинки до уявної її товщини.
ПОРЯДОК РОБОТИ. 1. Виміряти мікрометром дійсну товщину скляної пластинки h в тому місці, де нанесені штрихи. 2. Визначити уявну товщину скляної пластики а, для чого пластинку покласти на столик мікроскопа під об‘єктив так, щоб обидва штриха перетинали оптичну вісь приладу. 3. Рухаючи тубус, досягти чіткого зображення видимого в мікроскопі штриха, нанесеного на верхню поверхню пластинки. Записати відлік мікрометра.
4. Опускати тубус мікроскопу до тих пір, поки не отримається чітке зображення штриха на нижній стороні пластинки. Різниця відліків мікрометричного гвинта дає уявну товщину пластинки а. 1) Обчислити показник заломлення по формулі: 1. Вимірювання дійсної і уявної товщини провести не менше п‘яти разів. Визначити середнє значення показника заломлення скла та обчислити похибку вимірювань. Результат записати у вигляді:
КОНТРОЛЬНІ ЗАПИТАННЯ. 1. Сформулюйте закони відбивання і заломлення світла. 2. Дайте визначення фазової швидкості світла. 3. Що називається відносним показником заломлення речовини? 4. Що називається абсолютним показником речовини? 5. Від чого залежить показник заломлення речовини? 6. Коли спостерігається явище повного відбивання світла? 7. Показати хід променів через систему: повітря–вода–скло–повітря. 8. Чи залежить показник заломлення скла від товщини пластинки? 9. Чому при розгляданні предмета через плоскопаралельну пластинку він здається розміщеним ближче, ніж в дійсності?
Лабораторна робота № 3 ТЕОРЕТИЧНІ ВІДОМОСТІ Для визначення головної фокусної віддалі збірної лінзи і системи лінз користуються методом Гауса- Беселя. Для цієї мети можна користуватись формулою тонкої лінзи. 1/F = 1/d + 1/f (1) де d – віддаль від предмета до оптичного центру лінзи; f – віддаль від оптичного центру лінзи до різкого зображення цього предмета на екрані; F – головна фокусна віддаль лінзи. Величини d і f на практиці не можна визначити чітко тому, що у загальному вигляді положення центру лінз невідомо. Якщо на місці чіткого зображення предмета помістити сам предмет, то його зображення отримаємо на тому місці, де раніше знаходився предмет. При цьому значення F в формулі (1) не змінюється тому, що d і f входять в формулу симетрично. В дійсності, в досліді Гауса-Беселя переміщення предмета не робиться. Отримавши різке зображення предмета (перевернуте та збільшене) на екрані АВ вимірюють віддаль від предмета до екрана D. Пересувають лінзу L в положення L’ так, щоб отримати різке зображення предмета, але вже зменшене (Мал.1) А’В’.
Мал.1. Таким чином, за допомогою однієї і тієї ж лінзи одержують два зображення: одне збільшене, яке знаходиться на віддалі f від лінзи, а друге-зменшене, на віддалі f’=d від лінзи. Зміщення оптичного центру лінзи O на рис.1 позначено через a. Величину a можна вимірювати переміщенням будь-якої точки лінзи L тому, що при її переміщенні положення оптичного центра відносно лінзи не змінюється. З мал.1 видно:
D = /d/ +/f/, a = /f/ - /d/ (2) Звідси знаходимо Застосовуючи формулу (1) одержимо:
ПОРЯДОК РОБОТИ Завдання 1: Визначення головної фокусної віддалі збірної лінзи. 1. Закріпити досліджувану лінзу на рейтері оптичної лави. 2. Ввімкнути освітлювач. Переміщуючи лінзу, досягти різкого зображення предмета на екрані (збільшеного) і зафіксувати положення лінзи. 3. Знову пересунути лінзу і досягти нового зображення предмета на екрані (зменшеного). 4. Виміряти величини D і а. 5. Досліди повторити 3-5 разів. 6. Дані вимірювань занести в таблицю. 7. Обчислити фокусну відстань збірної лінзи за формулою (3). 8. Обчислити похибку вимірювань.
Завдання 2. Визначення головної фокусної віддалі розсіювальної лінзи. 1. Розташувати збірну та розсіювальну лінзи як на мал.2, щоб комбінація лінз була збірною. Одержати чітке зображення на екрані. 2. Виміряти віддаль f’ від розсіювальної лінзи Lp до зображення на екрані Е1.
Мал.2. 3. Зняти розсіюючу лінзу Lp і одержати чітке зображення шкали освітлювача на екрані Е2. Виміряти віддаль d’ від екрана Е2 до місця, де розташувалась розсіююча лінза в комбінації (мал.2). 4. Дані вимірювань занести в таблицю і визначити F’ за формулою: 1/F’=1/f’ + 1/d’ (4) 5. Дослід повторити 3-5 разів, змінюючи відстань між лінзами Lз та Lр. 6. Обчислити похибку вимірювань.
КОТРОЛЬНІ ЗАПИТАННЯ. 1. Дати означення лінзи, тонкої лінзи, оптичного центра, оптичної сили лінзи, фокусу лінзи. 2. Назвати основні параметри оптичної системи. 3. Яку систему називають центрованою оптичною системою? 4. Записати формулу тонкої лінзи. 5. Вміти будувати зображення в лінзах. 6. Вивести формулу (3).
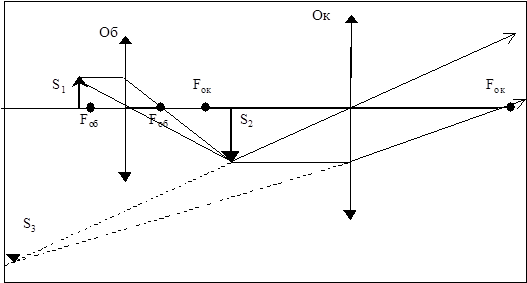
Лабораторна робота № 4. ТЕОРЕТИЧНІ ВІДОМОСТІ Людське око здатне роздільно розрізнити дві точки в тому випадку якщо кут, утворений прямими, які проходять через них і оптичний центр ока (кут зору) не менше 1 хвилини. Із зменшенням віддалі від предмета до ока кут зору збільшується. Однак існує мінімальна віддаль, на якій око здатне різко бачити предмет. В цьому випадку для розглядання дуже дрібних предметів потрібно збільшити кут зору, що досягається за допомогою мікроскопу. Хід променів в мікроскопі зрозумілий з Мал.1
Мал.1 Предмет S1, що розглядається, розміщується між фокусною та подвійною фокусною віддаллю об’єктива. Зображення S2, що утворене об’єктивом, розглядається в окуляр, як в лупу, тобто віддаль окуляр-зображення S2 менше фокусної віддалі Fок. Збільшення об’єктива: k1= S2 /S1 (1) Збільшення окуляра: k2= S3 /S2 (2) Збільшення мікроскопа: k = S3 /S1 (3) де k = k1 * k2, тобто збільшення мікроскопа дорівнює добутку збільшення окуляра і об’єктива. Якщо позначити віддаль між об’єктивом і окуляром через L, то збільшення мікроскопу можна знайти по відомій формулі:
Лабораторна робота №5 ТЕОРЕТИЧНІ ВІДОМОСТІ Телескоп (зорова труба) являє собою комбінацію оптичних систем – об’єктива і окуляра. Об’єктив, в якому завжди використовується позитивна лінза, утворює дійсне зображення предмета, яке розглядається оком через окуляр. Хід променів в астрономічній і земній зорових трубах показано на Мал. 1 і Мал. 2.
Мал.1.
Мал.2. На відміну від астрономічної зорової труби (труби Кеплера) галілеєва (або земна) труба має в якості окуляра розсіювальну лінзу і дає пряме зображення предмета. Зорові труби використовуються для спостережень віддалених предметів, що знаходяться на відстані, значно більшій фокусної віддалі об’єктива, тоді зображення предмета знаходиться практично в фокальній площині об’єктива. Особливістю телескопа є те, що віддаль між об’єктивом і окуляром дорівнює алгебраїчній сумі фокусних віддалей, тобто фокальні площини об’єктива і окуляра практично співпадають (див. F1, F2 на Мал. 1, 2). Внаслідок цього зображення, яке дає окуляр, являється збільшеним і знаходиться в нескінченності. Такий хід променів називається телескопічним. При спостереженні предметів за допомогою зорової труби кутовий розмір зображення, яке розглядається оком, виявляється значно більшим, ніж кутовий розмір предмета при спостереженні Відношення тангенсів кутів зору, під якими видні зображення та предмет, називається збільшенням оптичного приладу.
Можна переконатися, що збільшення телескопа дорівнює відношенню фокусних віддалей F1 і F2 об’єктива і окуляра.
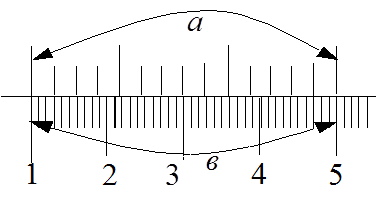
ПОРЯДОК РОБОТИ. Завдання 1. Скласти модель зорової труби та визначити її збільшення. 1. Встановити на оптичній лаві освітлювач, довгофокусну лінзу (№8) і зорову трубу з окулярним мікрометром так, щоб їх оптичні вісі співпадали. 2. Переміщуючи лінзу (№8) відносно освітлювача, домогтися, щоб вона працювала як конденсор, тобто промені виходили з неї паралельно. При цьому в зоровій трубі, що настроєна на нескінченність, буде видна шкала освітлювача. 3. Обертаючи окуляр зорової труби домогтись, щоб одночасно чітко були видні шкала освітлювача та шкала окулярного мікрометра. 4. Обчислити скільки поділок окулярної шкали припадає на один міліметр шкали освітлювача. Для цього знайти ті поділки, які співпадають на обох масштабах.(Мал.3).
Мал.3. Знайти відрізок а шкали освітлювача, що знаходиться між співпадаючими поділками.(на Мал.3 а =14
Лабораторна робота № 6 ТЕОРЕТИЧНІ ВІДОМОСТІ
Спостереження інтерференції за допомогою кілець Ньютона є найбільш простий метод вивчення цього явища та визначення довжини світлової хвилі. Кільця Ньютона спостерігаються в тому випадку, коли вигнута поверхня лінзи великого радіуса кривизни дотикається до плоскої, добре відполірованої пластинки: при цьому повітряний прошарок між ними поступово збільшується від центра до краю. Якщо на лінзу падає пучок монохроматичного світла, то світлової хвилі, відбиті від верхньої і нижньої границі цього повітряного прошарку будуть інтерферувати між собою. При цьому на екрані, розташованому за “кільцями Ньютона”, будемо мати таку картину: пляма в центрі буде світлою, а навколо неї – темні і світлі кільця, ширина яких зменшується. У відбитому світлі картина спостерігається зворотна картина – пляма в центрі буде темною, а всі світлі кола зміняться на темні і навпаки. Проведемо розрахунок кілець Ньютона в світлі, що проходить. Повна оптична різниця ходу
де
де rm - радіус m-того кільця і R – радіус кривизни лінзи. Умова утворення m-того кільця в світлі, що проходить, матиме вигляд
rm sm
Чим більше порядковий номер кільця, тим менше різниця між радіусами сусідніх кілець, тим тісніше кільця. Для радіуса темного кільця в світлі, що проходить, будемо мати:
З формул (4) і (5) можна визначити R або l. Проте, внаслідок пружної деформації скла неможливо домогтись дотику сферичної лінзи і плоскої пластини строго в одній точці, тому більш вірний результат отримаємо, якщо вирахувати R або l по різниці радіусів двох кілець:
ОПИС УСТАНОВКИ. Для зручності вимірювання радіуси кілець визначаються на екрані, куди вони проектуються. Для переходу до дійсних розмірів потрібно врахувати збільшення оптичної системи.
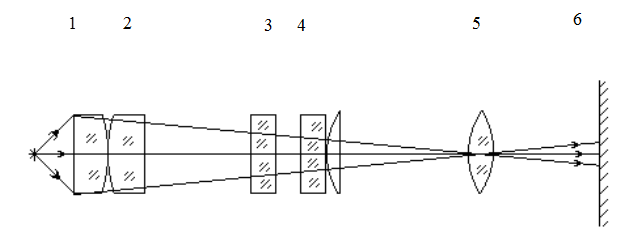
Мал.2. На оптичній лаві встановлені прилади в такій послідовності: джерело світла (1), конденсор (2), світлофільтр (3), кільця Ньютона (4), об‘єктив (5), екран(6). Отримавши чітке зображення кілець Ньютона на екрані, визначають збільшення, яке дає оптична система по формулі:
де D - середнє значення діаметра світлої плями на екрані, d – середнє значення діаметра лінзи в приладі “кільця Ньютона”. Формулу (6) можна записати, замінивши радіуси через діаметри
ПОРЯДОК РОБОТИ. 1. Скласти установку “кільця Ньютона” згідно мал.2. 2. Виміряти діаметри декількох темних кілець на екрані в зеленому світлі.
При зеленому світлі:
r1 = 8 мм, r2 = 14 мм, r3 = 19 мм, r4 = 24 мм;
3. Виміряти діаметри d і D лінзи, та її проекції на екрані. Визначити збільшення системи N.
d = 3 см, D = 7.5 см, N =
4. За формулою (6) визначити радіус кривизни лінзи.
Для m = 2 i n = 1: R1= Для m = 3 i n = 1: R2= Для m = 3 i n = 2: R3= Для m = 4 i n = 1: R4= Для m = 4 i n = 2: R5= Для m = 4 i n = 3: R6= Rсер.= 49.5 м.
tα = 3.2, α = 95% Отже, ∆R = 6.2 м; Rсер.= (49.5 ± 6.2) м.
5. Не змінюючи віддалі між приладами, виміряти проекцію діаметра 2-го, 3-го, 4-го, 5-го кілець при червоному світлі. Знаючи довжину хвилі зеленого світла l=550 нм, знайти довжину хвилі червоного світла, користуючись відношенням lчер/lзел = (rm2 – rn2)чер /(rm2 __ rn2)зел (9).
При червоному світлі:
r1 = 9 мм, r2 = 15 мм, r3 = 20 мм, r4 = 24 мм.
З рівності (9) маємо:
Для m = 2 i n = 1: λчер.1 = 550*10-9*((0.015 м)2-(0.009 м)2)/((0.014 м)2-(0.008 м)2) = 600 нм. Для m = 3 i n = 1: λчер.2 = 550*10-9*((0.02 м)2-(0.009 м)2)/((0.019 м)2-(0.008 м)2) = 591 нм. Для m = 4 i n = 1: λчер.3 = 550*10-9*((0.024 м)2-(0.009 м)2)/((0.024 м)2-(0.008 м)2) = 532 нм. Для m = 3 I n = 2: λчер.4 = 550*10-9*((0.02 м)2-(0.015 м)2)/((0.019 м)2-(0.014 м)2) = 583 нм. Для m = 4 i n = 2: λчер.5 = 550*10-9*((0.024 м)2-(0.015 м)2)/((0.024 м)2-(0.014 м)2) = 508 нм. Для m = 4 I n = 3: λчер.6 = 550*10-9*((0.024 м)2-(0.02 м)2)/((0.022 м)2-(0.019 м)2) = 490 нм.
λчер.сер. = 564 нм. 6. Обчислити похибку вимірювань, вважаючи похибку lзел відомою: lзел= 550 ±30 нм.
tα = 3.2, α = 95%
λчер. сер. = (564 ± 120) нм.
7.
КОНТРОЛЬНІ ЗАПИТАННЯ 1. Пояснити, як відбувається інтерференція світла при відбиванні від прозорої пластинки. 2. Що називають смугами рівної товщини та смугами рівного нахилу? 3. Як змінюється інтерференційна картина від тонкої плівки, якщо її розглядати в світлі, що проходить? 4. Чому радіус кривизни лінзи повинен бути великим? 5. Як змінюється інтерференційна картина, якщо проміжок між лінзою і пластинкою заповнити рідиною? 6. Чому дорівнює оптична різниця ходу відбитих і заломлених променів в “кільцях Ньютона”? 7. Вивести формулу (9). 8. Як треба змінити схему досліду, щоб спостерігати кільця Ньютона у відбитому світлі?
Лабораторна робота № 7. ТЕОРЕТИЧНІ ВІДОМОСТІ. Накладання світлових хвиль, в результаті якого в одних точках виникають коливання з максимальною амплітудою, а в інших - з мінімальною, називається інтерференцією світла. Для одержання інтерференції необхідно, щоб світлові хвилі, які випромінюються джерелом, були когерентними, тобто щоб коливання від них мали сталу різницю фаз. Когерентні хвилі можна одержати за допомогою біпризми Френеля. Хід променів в біпризмі показаний на Мал.1.
Мал.1. Біпризма ABС являє собою оптичну систему з двох призм з малими кутами заломлення З інтерференційної картини можна визначити довжину світлової хвилі:
де r - відстань від щілини до біпризми (див. мал.2); d - відcтань від щілини до лінзи; B - стала біпризми; DC – ширина інтерференційної смуги. Звичайно На екрані спостерігається k смуг, які мають загальну ширину l. Тоді:
Якщо відстань лінза - екран, при якій спостерігається картина, дорівнює а, то при оптичній силі D формулу (1) можна записати:
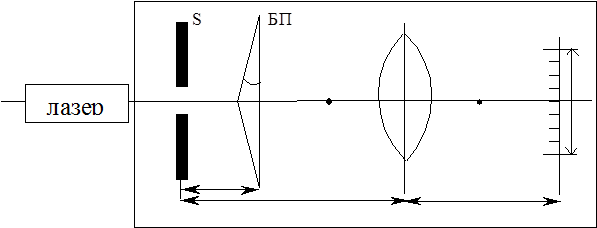
ОПИС УСТАНОВКИ. Установка складається з оптичної лави, на якій послідовно розміщені лазер, щілина, біпризма, лінза, екран (Мал.2). Всі вони юстовані відносно однієї оптичної осі (якою є промінь лазера).
Мал.2. Біпризма (БП) виготовлена з скла, показник заломлення якого n= 1,85 і має заломлюючий кут α =15' або 4,36·10-3 рад. В розрахунках використовується біпризма, постійна якої B рівна
Лінза (Л2) має фокусну віддаль ~3 см і оптичну силу D= 33 діоптрії. Лінза встановлена так, щоб інтерференційна картина від двох пучків, заломлених біпризмою, утворилась безпосередньо перед переднім фокусом лінзи. Це дозволяє спостерігати на екрані (Е) збільшену інтерференційну картину.
ПОРЯДОК РОБОТИ. 1. Встановити прилади згідно Мал. 2. УВАГА: лазер вмикає викладач (лаборант) після перевірки схеми. 2. Відрегулювати ширину щілини і її розміщення відносно променя лазера так, щоб отримати на екрані картину смуг загальною шириною близько 2 см. 3. Виміряти віддалі r, d, a, l і кількість смуг k. 4. Результати занести в таблицю. 5. Пункти 2 і 3 повторити не менше 5 разів. 6. По формулі (2) обчислити довжину хвилі для кожного досліду. Результати занести в таблицю.
1. Обчислити похибку вимірювань.
λсер = (796 ± 71) нм. (tα = 4.3, α = 95%)
КОНТРОЛЬНІ ЗАПИТАННЯ. 1. В чому полягає явище інтерференції? 2. Чому не спостерігається інтерференція від двох незалежних джерел світла? 3. Назвіть методи одержання когерентних світлових хвиль. 4. Накресліть хід променів в біпризмі Френеля. 5. Запишіть умови виникнення максимумів і мінімумів інтерференції. 6. Поясніть, що таке просторова та часова когерентність. 7. Які методи спостереження інтерференції Ви знаєте?
Лабораторна робота № 8. ТЕОРЕТИЧНІ ВІДОМОСТІ. В інтерферометрі Релея використовується дифракція Фраунгофера на двох щілинах (мал.1). розрахунок інтенсивності світлових коливань після проходження двох щілин можна зробити, використавши принцип Гюйгенса-Френеля.
Мал.1. Інтенсивність світлових коливань на екрані записується виразом:
де І0- інтенсивність світла в центрі дифракційної картини від однієї щілини; k - хвильовий вектор, Перший множник в (1) дає інтенсивність при дифракції на одній щілині шириною b, а другий - інтерференцію хвиль на двох щілинах, розташованих на відстані d. Розподіл інтенсивності на екрані для цього випадку приведений на мал..2 (пунктирна лінія – дифракційна картина від однієї щілини).
Мал.2. Практичний інтерес мають яскраві інтерференційні смуги, розташовані в межах центрального дифракційного максимуму, тобто в області Число смуг в цій області (головних максимумів) залежить від відстані між щілинами d. Очевидно, чим більше d, тим більше число смуг спостерігається в згаданому інтервалі. Мал.2 відповідає інтерференційній картині в монохроматичному світлі. Якщо щілини освітлюються білим світлом, то всі смуги, крім центральної, будуть забарвленими. Таким чином, центр інтерференційної картини візуально визначається як біла смуга, обмежена чорними мінімумами.
КОНСТРУКЦІЯ ІНТЕРФЕРОМЕТРА. Інтерферометр складається з коліматора (щілина S і об‘єктив О1) подвійної щілини Д та зорової труби (об‘єктив О2 ,окуляр О). Щілина S освітлюється лампою розжарення Л через конденсор К. Ця щілина розташована в фокусі об‘єктива О1. Світло, що проходить, через цей об‘єктив, падає на подвійну щілину Д паралельним пучком (плоска хвиля), що забезпечує виконання умов дифракції Фраунгофера при невеликих розмірах установки. Дифракційна картина отримується в фокальній площині об‘єктива О2 і розглядається через окуляр О. Кожному значенню дифракційного кута j в фокальній площині об‘єктива О2 відповідає лінія, що паралельна щілинам, яка відстоїть від оптичної вісі на відстані
де f – фокусна відстань об‘єктива О2. Відстань між інтерференційними смугами
Звичайно f= 50 см., d= 1 cм., тобто
Мал.3. Інтерферометр Релея може застосовуватись для визначення невеликих змін показників заломлення рідин і газів, визначення домішок різних газів в повітрі (зокрема для вимірювання концентрації рудничних газів в шахтах). Суть методу полягає в тому, що на шляху світлових хвиль розміщується два прозорих об‘єкта, наприклад, дві кювети з різними рідинами (мал.3). Це приводить до появи різниці ходу між променями В ІТР-1 для зміщення інтерференційної картини в горизонтальній площині використовується компенсатор Жамена, що складається з двох однакових плоско-паралельних пластин. Нахилом однієї з них можна одержати додаткову різницю ходу В окулярі ІТР-1 видно не одну, а дві системи інтерференційних смуг. Верхня система смуг рухома. Вона утворюється при інтерференції променів, які пройшли під кюветою і компенсатором. Для роздільного спостереження двох систем в окулярі застосована не сферична, а циліндрична оптика.
ПОРЯДОК РОБОТИ.
1. Вивчити інструкцію до приладу ІТР-1. 2. Ввімкнути освітлювач інтерферометра і впевнитись, що в полі зору спостерігаються дві системи смуг інтерференційної картини. 3. Перед початком вимірювань слід прокалібрувати компенсатор та встановити початок відліку. Для цього кювети 2-3 рази промивають дистильованою водою, встановлюють їх в інтерферометр та помічають поділки барабана компенсатора (мікрометричного гвинта). Суміщення проводять по центральній (нульовій) смузі. Цей відлік мікрометричного гвинта N0 є початком відліку для подальших вимірювань (0 кювети). Для градуювання компенсатора послідовно суміщають перш
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.150.38 (0.017 с.) |

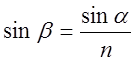 (4)
(4)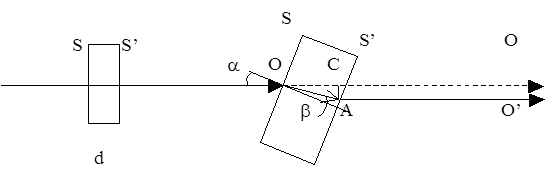

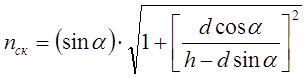 (5)
(5)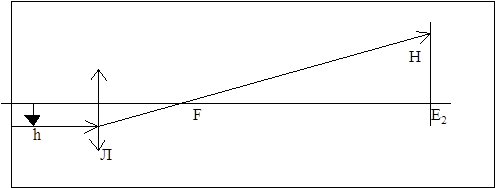
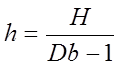 (6),
(6),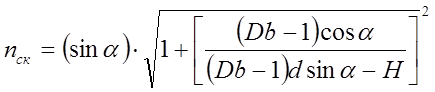 (7)
(7)
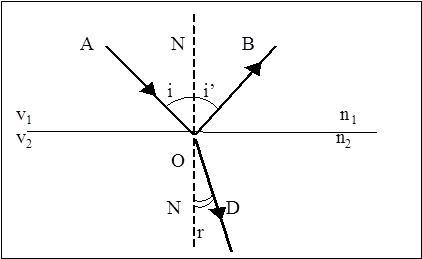
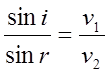 (1)
(1) ;
; 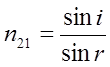 (2)
(2)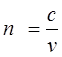 ;
;  (3)
(3) - фазова швидкість в даному середовищі 2.
- фазова швидкість в даному середовищі 2.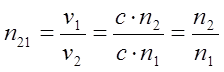 (4)
(4)
 (5)
(5)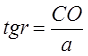 ;
; 

 .
.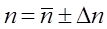 .
.
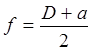
 (3)
(3)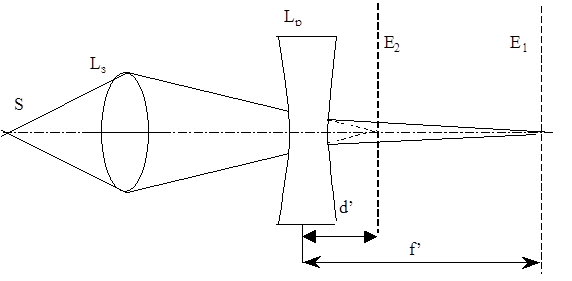

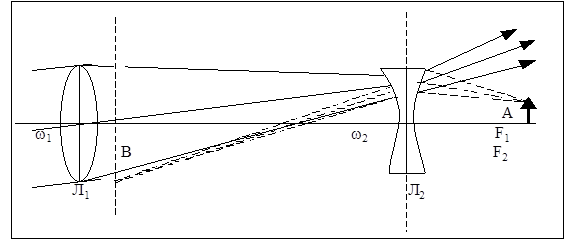
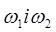 на Мал. 1, 2).
на Мал. 1, 2).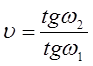 (1)
(1)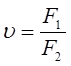 (2)
(2)
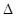 :
: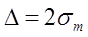 (1),
(1),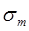 - товщина повітряного прошарку. Легко підрахувати з геометричних побудов (Мал.1)
- товщина повітряного прошарку. Легко підрахувати з геометричних побудов (Мал.1)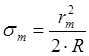 (2)
(2)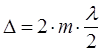 (3),
(3), (4).
(4).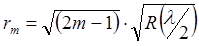 (5).
(5).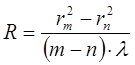 (6).
(6).
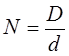 (7),
(7),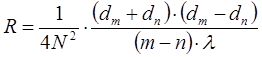 ;
;  (8).
(8).
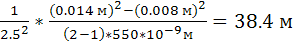 .
.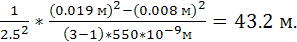
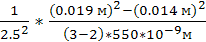 = 48 м.
= 48 м.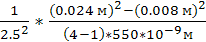 = 49.7 м.
= 49.7 м.
 = 62.6 м.
= 62.6 м.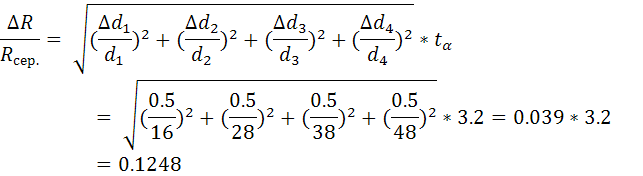
 чер =
чер =  (rm2 – rn2)чер /(rm2 __ rn2)зел
(rm2 – rn2)чер /(rm2 __ rn2)зел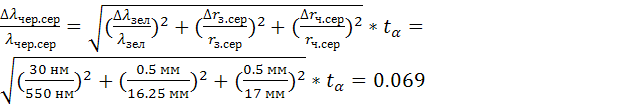 *3.2 = 0.22
*3.2 = 0.22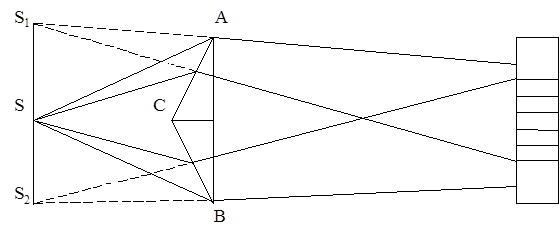
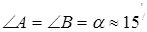 , які з’єднані своїми основами. Якщо промені від щілини S, що забезпечує просторову когерентність пучка світла і паралельна ребру С, падають на біпризму Френеля, то внаслідок заломлення вони розділяються на два пучки, що перетинаються за призмою. Продовження заломлених променів перетинаються в точках S1 і S2, які є уявними зображеннями щілини S і можуть розглядатись як когерентні джерела світла. В області накладання заломлених світлових хвиль можна спостерігати інтерференційну картину в вигляді темних і світлих смуг, що чергуються. Максимум нульового порядку інтерференції знаходиться на оптичній вісі системи, яка проходить через щілину S та ребро С біпризми.
, які з’єднані своїми основами. Якщо промені від щілини S, що забезпечує просторову когерентність пучка світла і паралельна ребру С, падають на біпризму Френеля, то внаслідок заломлення вони розділяються на два пучки, що перетинаються за призмою. Продовження заломлених променів перетинаються в точках S1 і S2, які є уявними зображеннями щілини S і можуть розглядатись як когерентні джерела світла. В області накладання заломлених світлових хвиль можна спостерігати інтерференційну картину в вигляді темних і світлих смуг, що чергуються. Максимум нульового порядку інтерференції знаходиться на оптичній вісі системи, яка проходить через щілину S та ребро С біпризми. (1),
(1),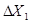 мала і для її спостереження використовують лінзу, одержуючи збільшене зображення на екрані.
мала і для її спостереження використовують лінзу, одержуючи збільшене зображення на екрані.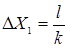
 (2)
(2)

 = 0.089
= 0.089
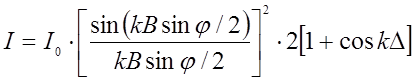 (1),
(1), різниця ходу променів від двох щілин.
різниця ходу променів від двох щілин.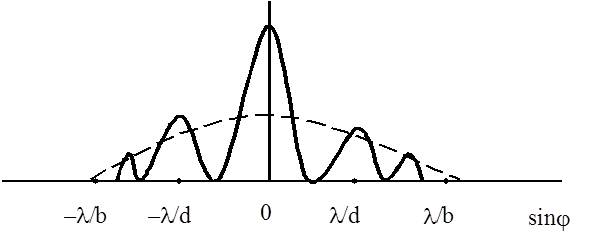
 | sin φ|
| sin φ|  / b.
/ b.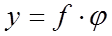 ,
, в фокальній площині рівна:
в фокальній площині рівна: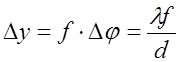 (2)
(2)
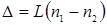 , де L – товщина шару рідини, n1 і n2 – показники заломлення двох рідин. Внаслідок інтерференції променів з різницею ходу
, де L – товщина шару рідини, n1 і n2 – показники заломлення двох рідин. Внаслідок інтерференції променів з різницею ходу  інтерференційна картина зміщується в горизонтальній площині відносно оптичної системи приладу.
інтерференційна картина зміщується в горизонтальній площині відносно оптичної системи приладу. . При
. При