
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Колебания без затухания.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тема 1. Колебания без затухания. П.1. Периодический процесс. Гармонические колебания. Звук Процессы, происходящие в природе, очень часто имеют регулярно повторяющиеся части (с той или иной степенью точности). Повторяются дни и ночи, времена года, движение Луны, Солнца и звезд, и т.д. Большое значение имеют повторяющиеся процессы в технике. Проблема: Каковы основные характеристики повторяющихся процессов и какими уравнениями они связаны? Решение: В первую очередь обратимся к механическим процессам, части которых регулярно повторяются. Периодическим (колебательным) называется процесс, часть которого регулярно повторяется во времени. колебательной называют систему тел, в которой происходит периодический процесс. полным колебанием называется минимальная часть периодического процесса, которая полностью повторяется. периодом T называется длительность одного полного колебания. Замечание: через время, равное Т, процесс полностью повторяется.A(t) = A(t±nT), где n = 1, 2, 3, … есть любое целое число. Оно может начинаться с любой точки графика A(t) зависимости физической характеристика А от времени t. Замечание: Периодический процесс есть абстракция (модель), т.к. он бесконечен во времени. Частный случай периодического процесса – гармоническое колебание (ГК). Гармоническим называется колебание, при котором физическая характеристика A(t) меняется по закону синуса или косинуса.
Если «А» есть характеристика движения, тогда колебание называется механическим. Первая характеристика движения – положение. Закон движения, если тело движется по оси Х по гармоническому закону, выглядит так:
Идеальное гармоническое колебание есть абстрактная модель процесса, т.к. оно бесконечно во времени. Но оно является хорошим приближением для исследования реальных процессов, длительность которых много больше периода. Звук Характеристики гармонических колебаний: Аm - амплитуда есть максимальное отклонение характеристики А от нулевого значения; φ(t) = φ0 - начальная фаза - значение аргумента косинуса (или синуса) в начальный момент времени t0 = 0;
В этих обозначениях закон движения будет выглядеть так: x(t) = xm cos(wt + j0). Графически:
Еще одна очень важная характеристика:
Замечание. Гармоническое колебание это абстракция (модель), поскольку оно имеет вид точной математической функции (синусоиды), которая бесконечна во времени. Вопрос: Если гармоническое колебание есть абстракция, зачем же мы его исследуем? Ответ: Математика позволяет заменить задачу о произвольном периодическом процессе на задачу о гармонических процессах. Любая периодическая функция раскладывается в ряд Фурье (есть сумма гармонических функций). Дополнение. Напомню вид графической зависимости для некоторых широко используемых реальных воздействий:
t Импульс.
t
Отрезок синусоиды.
Воздействие таких сил можно рассматривать, как сумму (интеграл) воздействий отдельных гармонических составляющих (теорема Фурье). Поэтому мы должны их изучить в первую очередь.
Звук
Алгоритм применения разложения Фурье. 1. Реальное воздействие представляют, как совокупность гармонических воздействий (раскладывают в ряд или интеграл Фурье и находят амплитуды каждой гармонической силы). 2. Рассматривают воздействие каждой гармонической силы на исследуемую систему и вычисляют результат. 3. Суммируют (интегрируют) результаты и получают искомый результат от исходного воздействия. П.3. Пружинный маятник Звук Проблема: Как применять полученные результаты для решения вопроса о возможности колебаний и их характеристиках? Решение: 1) использовать известные физические законы, которым подчиняется данная система, 2) трансформировать их, стремясь получить дифференциальное уравнение колебаний для какой-нибудь характеристики этой системы. Если это удалось – колебания возможны. Пример. Проанализируем движение шарика на пружинке. В качестве модели шарика используем МТ, а пружинку будем считать идеальной, т.е. невесомой и абсолютно упругой. Пусть шарик лежит на идеально гладкой горизонтальной поверхности, пружина соединяет его с массивной стенкой.
Жесткость пружины – k; m – масса шарика. Растянем пружину, тогда возникнет сила упругости.
Основные законы:
Далее запишем закон Гука:
Конкретизируем второй закон Ньютона:
Учтем, что
Сравнивая с дифференциальным уравнением (*), делаем вывод, что они похожи и, следовательно, 1. В такой системе возможны гармонические колебания
2. Частота этих колебаний определяется жесткостью пружины k и массой шарика m: Замечание: Амплитуда и начальная фаза определяются дополнительными условиями.
П.3. Вынужденные колебания Звук Проблема: Как возникают колебания и чем они поддерживаются? Известно: Движение возникает и изменяется при наличии внешнего воздействия. Значит, надо исследовать колебательную систему, на которую что-то действует. Вынужденными называются колебания, возникающие при наличии внешнего воздействия. Оно может быть описано с помощью внешней силы. Второй закон Ньютона будет выглядеть так:
Внешняя сила – функция времени. В системе должна быть квазиупругая сила и действовать сила трения.
Для физической характеристики “A”.
Такое дифференциальное уравнение имеет решение, равное сумме двух функций (см. математику). При t ® ¥ решение оказывается близким к гармоническому, если F(t) - гармоническая функция
ПРИМЕР: Упругий маятник с вязким трением.
τ- постоянная времени установления колебаний. Огибающая имеет вид 1 – exp(-t/t). Касательная к ней, проведенная в начальный момент времени пересекает ось времени в точке t = t. Через 3τ колебания становятся практически установившимися и закон движения будет
Установившийся режим – в нем происходят колебания с частотой вынуждающей силы и постоянной амплитудой. Амплитуда установившихся колебаний
ВЫВОД: Амплитуда установившихся колебаний зависит от: - амплитуды внешней силы, - от частоты внешней силы, частоты собственных колебаний и коэффициента затухания.
Звук
ЗАДАЧА: проанализировать зависимость амплитуды установившихся колебаний от частоты вынуждающей силы. Рассмотрим график соответствующей зависимости:
Если на систему действует постоянная сила (т.е. W = 0), появляется постоянное смещение Затем, при увеличении частоты внешней силы амплитуда сначала растет, достигает максимума, а затем асимптотически стремится к 0.
Максимум амплитуды колебаний наблюдается при определенной частоте Ω0 внешней силы, где
Ω0 =
Резонанс – резкое увеличение амплитуды вынужденных колебаний, при приближении частоты вынуждающей силы к некоторому (резонансному) значению. Добротность показывает, как резко увеличивается амплитуда при резонансе:
При d = 0 Q → ∞.
Тема 1. Колебания без затухания.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 629; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.146.157 (0.011 с.) |

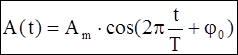 - общий вид закона изменения характеристики A при гармонических колебаниях.
- общий вид закона изменения характеристики A при гармонических колебаниях.
 .
. – фаза, есть значение аргумента косинуса (или синуса) в произвольный момент времени «t»;
– фаза, есть значение аргумента косинуса (или синуса) в произвольный момент времени «t»; - циклическая частота.
- циклическая частота. υ = w/2p = 1/Т - частота, есть количество полных колебаний за 1с. Иначе: ω = 2πυ.
υ = w/2p = 1/Т - частота, есть количество полных колебаний за 1с. Иначе: ω = 2πυ. F
F F
F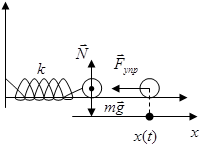 Y
Y - второй закон Ньютона.
- второй закон Ньютона. .
. . Подставим силу упругости
. Подставим силу упругости = 0.
= 0. .
. такую систему будем называть пружинный маятник.
такую систему будем называть пружинный маятник. .
. .
.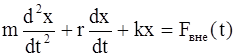

 .
.
 .
. ,
,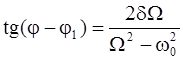 .
.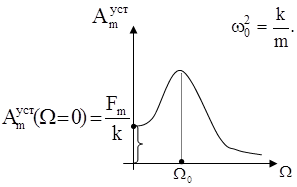
 .
.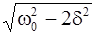 .
. .
.


