
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П.4. Гармонический осциллятор. Математический маятник.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Звук Вопрос: Какие еще полезные задачи можно также легко решить, используя наши знания? Пример 1: Движение при наличии квазиупругой силы. Определение. Если на тело действует сила, формула для которой похожа на закон Гука, тогда такая сила называется квазиупругой. Закон Гука: Квазиупругая сила FX = - const×x = - kx. Тело совершает гармонические колебания с циклической частотой Движение в параболической «потенциальной» яме. Потенциальная энергия сжатой пружины
Тело массы m, находящееся в такой яме, может совершать гармонические колебания с частотой
Пример 2. Математический маятник. Это модель, состоящая из МТ, подвешенной на идеальной нити (невесомая, нерастяжимая), находящейся в однородном гравитационном поле, и совершающей малые отклонения от положения равновесия. Используем второй закон Ньютона для МТ, движущейся по окружности. Запишем его для угловых характеристик движения:
L
j X
В соответствии со вторым законом Ньютона
Выбираем ось Х вдоль вектора ускорения, направленного перпендикулярно нити и являющегося тангенциальным. После проектирования на ОХ имеем max = - mg Sin(j).
Звук
Далее используем условие малости угла отклонения (Sin(j) = j) и уравнение связи углового и линейного ускорений at = eR. Кроме того, ах = аt:
отсюда получим (учитывая, что R = L)
Закон движения, для угла отклонения нити от вертикали, выглядит так: j(t) = jm cos(wt + j0).
Вывод: математический маятник может совершать гармонические колебания!
Замечание: Циклическая частота колебаний математического маятника определяется полученной нами формулой
Эта формула, хорошо нам знакома из курса элементарной школьной физики, где она была приведена без вывода. Теперь мы видим, что она не относится к фундаментальным законам физики, а может быть выведена из действительно фундаментального второго закона Ньютона с учетом свойств кинематических характеристик движения МТ.
Тема 2. Свободные затухающие колебания. Вынужденные колебания. Сложение колебаний
П.1. Свободные затухающие колебания. Звук Проблема: Могут ли свободные колебания в реальной механической системе продолжаться бесконечно долго? Решение: Надо исследовать реальную систему, в которой действуют силы, уменьшающие амплитуду колебаний. Затухающими называются колебания, амплитуда которых асимптотически стремится к нулю.
Зависимость амплитуды от времени:
Ao(0) Ao(0) ·e - d·t Ao(t)
A0(t) =
A(t) =
t - постоянная времени затухания колебаний. Это время, в течение которого амплитуда убывает в «e» раз и становится равной 0,37 За время, равное 3t, амплитуда колебаний становится пренебрежимо малой и колебания «исчезают», «прекращаются», «затухают». Дифференциальное уравнение затухающих колебаний характеристики А:
Решение этого уравнения:
Вопрос: в какой механической системе возможны свободные затухающие колебания? Пусть физическая характеристика А есть координата х МТ, тогда для механических затухающих колебаний
Звук Перепишем, используя определения ускорения и скорости:
Вспомним второй закон Ньютона: По закону Гука FУПР.Х = - k x, и
Подставляем в (*) и получаем:
FТР.Х = - rv это сила вязкого трения, пропорциональная скорости и направленная против движения.
Вывод: Если у нас есть механическая система - модель которой упругий маятник и если в нем возникает сила вязкого трения, то в такой системе возможны свободные затухающие колебания.
Сила вязкого трения в векторном виде:
Рассмотрим эту силу более детально.
1) r = const. (коэффициент вязкого трения) 2) 3) 4)
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 598; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.187.71 (0.01 с.) |

 .
. .
. .
.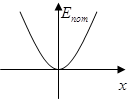 Если на тело действует квазиупругая сила,
Если на тело действует квазиупругая сила, 


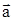 t
t или
или  .
.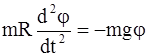 ,
, , или
, или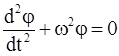 , где
, где  .
.

 Ao(t)
Ao(t) - амплитуда, зависящая от времени,
- амплитуда, зависящая от времени, - коэффициент затухания,
- коэффициент затухания,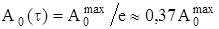 - амплитуда в момент t = t.
- амплитуда в момент t = t.
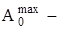 максимальная амплитуда (при t = 0).
максимальная амплитуда (при t = 0).
 .
. , где
, где  .
. .
. умножим и перегруппируем:
умножим и перегруппируем: .
. (*), слева у нас все так же. А что справа?
(*), слева у нас все так же. А что справа? .
.
 .
.


 и
и  .
.


