
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скорость и ускорение при гармонических колебаниях.Содержание книги
Поиск на нашем сайте
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями. Согласно определению скорости, скорость – это производная от координаты по времени. Согласно определению ускорения, ускорение – это производная от скорости по времени. Гармонические колебания - колебания, при которых колеблющаяся величина изменятся со временем по закону синуса (косинуса). Гармонические колебания описываются уравнением типа: s – смещение колеблющейся точки от положения равновесия. А - максимальное значение колеблющейся величины, называемое амплитудой колебания ω0 — круговая (циклическая) частота, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А. Дифференциальное уравнение гармонических колебаний материальной точки.
Пружинный маятник Колебательная система в этом случае представляет собой совокупность некоторого тела и прикрепленной к нему пружины. Пружина может располагаться либо вертикально (вертикальный пружинный маятник), либо горизонтально (горизонтальный пружинный маятник).
где ах – ускорение, m - масса, х - смещение пружины, k – жесткость пружины. Это уравнение называют уравнением свободных колебаний пружинного маятника. Оно правильно описывает рассматриваемые колебания лишь тогда, когда выполнены следующие предположения: 1)силы трения, действующие на тело, пренебрежимо малы и поэтому их можно не учитывать; 2) деформации пружины в процессе колебаний тела невелики, так что можно их считать упругими и в соответствии с этим пользоваться законом Гука. Закон Гука, устанавливает линейную зависимость между упругой деформацией твердого тела и приложенным механическим напряжением. Напр., если стержень длиной l и поперечным сечением S растянут продольной силой F, то его удлинение = Fl/ ES, где E — модуль упругости (модуль Юнга).
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1480; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.006 с.) |

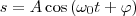 , где
, где
 (2)
(2)  (3)
(3) 
 (4)
(4)  (5)
(5)  , или, где m – масса точки, k – коэффициент квазиупругой силы (k=mw2).
, или, где m – масса точки, k – коэффициент квазиупругой силы (k=mw2).



