
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоемкость идеального газа. Уравнение Майера.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температурыδТ, которое при этом произошло. Для любого идеального газа справедливо соотношение Майера:
где R — универсальная газовая постоянная,
Уравнение Майера вытекает из первого начала термодинамики, примененного к изобарическому процессу в идеальном газе:
в рассматриваемом случае:
. Очевидно, уравнение Майера показывает, что различие теплоёмкостей газа равно работе, совершаемой одним молем идеального газа при изменении его температуры на 1 K, и разъясняет смысл универсальной газовой постоянной R — механический эквивалент теплоты.
Уравнение адиабаты идеального газа. Для 004050001801809030007идеальных газов, чью теплоёмкость можно считать постоянной, в случае 0902000708110010810510080901010511квазистатического процесса адиабата имеет простейший вид и определяется уравнением[ где: V — его 09011810объём, С учётом 031000200500805101101800818080405000180003003000700уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду:
где T — 00110018100018105000510011100абсолютная температура газа. Или к виду:
Поскольку Kвсегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении V) газ нагревается (T возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент K.
Политропические процессы. Политропический процесс, политропный процесс, изменение состояния физической системы, при котором сохраняется постоянной её 000803080010020500010001118теплоёмкость (С). Кривая на термодинамических диаграммах, изображающая П. п., называется 000803080010090008110000политропой. Простейшим примером обратимого П. п. может служить П. п. с 000803080010004050001801809030007идеальным газом, определяемый уравнением pVn = const, где р — давление, V — объем газа,
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.179.96 (0.009 с.) |


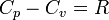 ,
, — молярная теплоёмкость при постоянном давлении,
— молярная теплоёмкость при постоянном давлении, — молярная теплоёмкость при постоянном объёме.
— молярная теплоёмкость при постоянном объёме. ,
,


 — 0900000700105018000408000100118показатель адиабаты,
— 0900000700105018000408000100118показатель адиабаты,  ,
,
 показатель политропы (Cp и Cv — теплоёмкости газа соответственно при постоянном давлении и объёме). Используя 000803080010031000200500805101101800818уравнение состояния идеального газа, уравнение политропы можно записать в ином виде:
показатель политропы (Cp и Cv — теплоёмкости газа соответственно при постоянном давлении и объёме). Используя 000803080010031000200500805101101800818уравнение состояния идеального газа, уравнение политропы можно записать в ином виде:  const или
const или  const (здесь Т — абсолютная температура).уравнение П. п. идеального газа включает, как частные случаи, уравнения: 00080308001000408000100100адиабаты (С =0, n = Cp/Cv, это отношение теплоёмкостей обозначают g), 00080308001000700100100изобары (С = Ср, n = 0), 000803080010007010100изохоры (С = Cv, n = ¥) и 00080308001000701051018изотермы (С = ¥, n = 1). Работа А идеального газа в П. п. против внешнего давления определяется по формуле
const (здесь Т — абсолютная температура).уравнение П. п. идеального газа включает, как частные случаи, уравнения: 00080308001000408000100100адиабаты (С =0, n = Cp/Cv, это отношение теплоёмкостей обозначают g), 00080308001000700100100изобары (С = Ср, n = 0), 000803080010007010100изохоры (С = Cv, n = ¥) и 00080308001000701051018изотермы (С = ¥, n = 1). Работа А идеального газа в П. п. против внешнего давления определяется по формуле  , где индексами 1 и 2 обозначены начальное и конечное состояния газа. Понятием П. п. широко пользуются в технической термодинамике при исследовании рабочих циклов тепловых двигателей.
, где индексами 1 и 2 обозначены начальное и конечное состояния газа. Понятием П. п. широко пользуются в технической термодинамике при исследовании рабочих циклов тепловых двигателей.


