Векторная диаграмма. Сложение параллельных колебаний одинаковой частоты.

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов.

1). Выберем некоторую направленную прямую - ось, вдоль которой будем откладывать колеблющуюся величину x.

2). Из взятой на оси некоторой точки О отложим направленный отрезок - вектор длины A, образующий с осью угол некоторый α.

3). Вращая вектор А вокруг точки О с угловой скоростью ω ₀, получим, что проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени: проекция конца вектора будет перемещаться по оси x, принимая значения от - А до + A, а координата этой проекции будет изменяться со временем по закону

Схему, полученную таким методом представления колебаний, называют векторной диаграммой.

Рассмотрим сложение двух гармонических колебаний х ₁ и x ₂ одного направления и одинаковой частоты: , (1)

Оба колебания представим с помощью векторов A ₁ и А ₂. Используя правила сложения векторов можно найти результирующий вектор А, представляющий собой сумму двух векторов A ₁ и А ₂.

Вектор A представляет собой результирующее колебание, потому что из рисунка видно, что проекция этого вектора на ось x равна сумме проекций складываемых векторов:

Вектор A вращается с той же угловой скоростью ω ₀, как и векторы А ₁ и А ₂, так что сумма x ₁ и х ₂ является гармоническим колебанием с частотой (ω ₀, амплитудой A и начальной фазой α. Используя теорему косинусов получаем, что

 

(2)

(3)

Замена сложения функций сложением векторов, которая возможна при Представление гармонических колебаний с помощью векторов, значительно упрощает вычисления.

 

Биения

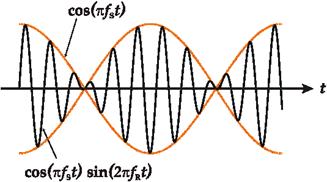
Биения — явление, возникающее при наложении двух гармонических колебаний близкой частоты и выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. Частота изменения амплитуды суммарного сигнала равна разности частот двух исходных сигналов.

Биения возникают от того, что один из двух сигналов постоянно отстаёт от другого по фазе и в те моменты, когда колебания происходят синфазно, суммарный сигнал оказывается усилен, а в те моменты, когда два сигнала оказываются в противофазе, они взаимно гасят друг друга. Эти моменты периодически сменяют друг друга по мере того как нарастает отставание.