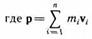Импульс системы материальных точек. Уравнение движения центра масс. Импульс и его связь с силой. Столкновения и импульс силы. Закон Сохранения Импульса.

Импульсом, или количеством движения материальной точки называется векторная величина, равная произведению массы материальной точки m на скорость ее движения v.

– для материальной точки;

– для системы материальных точек (через импульсы этих точек);

– для системы материальных точек (через движение центра масс).

Центром масс системы называется точка С, радиус-вектор r_C которой равен

,где

Уравнение движения центра масс:

Смысл уравнения таков: произведение массы системы на ускорение центра масс равно геометрической сумме внешних сил, действующих на тела системы. Как видим, закон движения центра масс напоминает второй закон Ньютона. Если внешние силы на систему не действуют или сумма внешних сил равна нулю, то ускорение центра масс равно нулю, а скорость его неизменна во времени по модулю и наплавлению, т.е. в этом случае центр масс движется равномерно и прямолинейно.

В частности, это означает, что если система замкнута и центр масс ее неподвижен, то внутренние силы системы не в состоянии привести центр масс в движение. На этом принципе основано движение ракет: чтобы ракету привести в движение, необходимо выбросить выхлопные газы и пыль, образующиеся при сгорании топлива, в обратном направлении.

Закон Сохранения Импульса

Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют

внешние силы, называется замкнутой (или изолированной). Если мы имеем механическую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направлены, т. е. геометрическая сумма внутренних сил равна нулю.

Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны т ₁, m ₂,..., т_n и v ₁, v ₂,..., v _n. Пусть F '₁, F '₂,..., F '_n — равнодействующие внутренних сил, действующих на каждое из этих тел, a f ₁, f ₂,..., F _n — равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:

d/dt(m₁v₁)= F '₁+ F ₁,

d/dt(m₂v₂)= F' ₂+ F ₂,

d/dt(m_n v _n)= F '_n+ F _n.

Складывая почленно эти уравнения, получим

d/dt (m₁ v ₁+m₂ v ₂+... + m_n v _n) = F '₁+ F '₂+...+ F ' _n + F ₁+ F ₂+...+ F _n.

Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то

d/dt(m₁v₁+m₂v₂ +... + m_nv_n)= F ₁ + F ₂+...+ F _n, или

dp/dt= F ₁+ F ₂+...+ F _n, (9.1)

где

импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему.

 

В случае отсутствия внешних сил (рассматриваем замкнутую систему)

Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т. е. закон со хранения импульса — фундаментальный закон природы.