
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные сведения об уравнении Ван-дер-ВаальсаСодержание книги
Поиск на нашем сайте
Нидерландский физик Ян Дидерик Ван-дер-Ваальс (1837 – 1923) – лауреат Нобелевской премии 1910 г., вывел в 1873 г. уравнение состояния неидеального газа в виде:
учитывающем конечность объема молекул и наличие сил межмолекулярного притяжения. Здесь a, b, R – постоянные, индивидуальные для каждого вещества;
b – поправка, учитывающая собственный объем молекул и силы отталкивания между ними.
Для определения индивидуальных постоянных, необходимы экспериментальные измерения Р, Т, V хотя бы для трех состояний. Часто численные значения постоянных a, b и R определяются по критическим параметрам вещества (Р К, Т К, V К), найденным экспериментально. В таблице 9.1. представлены значения критических параметров и коэффициента сжимаемости в критической точке Z К для некоторых веществ, где
Таблица 9.1. Критические параметры и Z К для некоторых веществ
На рис. 9.1. приведены изотермы Ван-дер-Ваальса. В области двухфазного состояния вещества (влажного насыщенного пара) они имеют волнообразный характер, что отличает их от реальных изотерм, представляющих прямые, параллельные оси V (например, С'С''). Эти волнообразные участки объясняются тем, что уравнение Ван-дер-Ваальса является уравнением третьей степени относительно V и, поэтому, может иметь либо три, либо один вещественный корень при различных Р и Т. Один вещественный корень существует только при
Рис. 9.1. Изотермы Ван-дер-Ваальса
В критической точке изотерма t КР имеет точку перегиба, поэтому в этой точке выполняются два условия:
и
Таким образом, для определения трех неизвестных постоянных (a, b и R) есть три уравнения, полученные из уравнений (9.1 – 9.3):
Температуру T К и удельный объем V К можно определить из уравнений (9.5), (9.6) и затем определить Р К из уравнения (9.4). В итоге
Отсюда
Найденное по формуле (9.8) значение R отличается от общепринятых значений, взятых по идеальному газу:
Так, для водяного пара при значениях T К, V К и Р К, взятых из таблицы 9.1, величина R по формуле (9.8) равна 297,2
Общим требованием ко всем уравнениям состояния реального газа является обращение их в уравнение Менделеева-Клайперона (PV = RT) при V → ∞. Уравнение Ван-дер-Ваальса при V >> b переходит в уравнение состояния идеального газа, если значение R взято по идеальному газу. Если брать R по идеальному газу, т.е. не определять ее по третьему уравнению (9.8), то для нахождения двух оставшихся постоянных (a и b) имеется три исходных уравнения (9.4), (9.5) и (9.6). Эта ситуация означает неопределенность в вычислении постоянных a и b, так как их значения зависят в этом случае от того, какая пара термодинамических параметров взята в качестве определяющих: Р К и Т К, V К и Т К, Р К и V К. В зависимости от выбора определяющей пары термодинамических параметров получаются различные значения постоянных a и b. В качестве примера в таблице 9.2 представлены результаты расчета постоянных Ван-дер-Ваальса для водяного пара при различных вариантах сочетания двух определяющих параметров.
Таблица 9.2. Значения постоянных Ван-дер-Ваальса для водяного пара при R = R μ/μ
При расчете R по формуле (9.8) при известных T К, V К и Р К получено: а = 706 Н∙м4/кг2, b = 0,001087 м3/кг. Предпочтительным является вариант 1 сочетания определяющих параметров, т.к. в специальных опытах по определению термодинамических параметров в критической точке, значения Р К и T К определяются значительно точнее, чем V К. Недостатком метода вычисления постоянных a и b при R, взятом по идеальному газу, является то, что критическая изотерма, рассчитанная по уравнению Ван-дер-Ваальса при всех трех вариантах сочетания определяющих параметров, не проходит через критическую точку. Ближе всего к ней проходит изотерма, рассчитанная при a и b, найденных по варианту 1. От этого недостатка свободен метод определения a, b и R по формулам (9.8), но при этом уравнение Ван-дер-Ваальса, записанное в форме
при Р → 0 не обращается в равенство, как у идеального газа, поскольку правая часть уравнения (9.9) не стремится к нулю. Кроме того, в этом методе коэффициент сжимаемости в критической точке ( Таким образом, определение постоянных уравнения Ван-дер-Ваальса через параметры T К, V К, Р К приводит к серьезным трудностям. Главная причина этих трудностей в том, что уравнение Ван-дер-Ваальса, строго говоря, удовлетворительно применимо лишь в области невысоких давлений, поэтому в области критической точки оно не отличается достаточной точностью, и описывает свойства реальных газов при высоких давлениях лишь приблизительно. Однако, это уравнение вполне применимо для качественных оценок при анализе некоторых закономерностей поведения реальных газов, в частности при дросселировании.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 , (9.1)
, (9.1) – поправка, учитывающая уменьшение давления из-за взаимного притяжения молекул; силы взаимного притяжения молекул создают в тонком слое у стенки сосуда равнодействующую силу, направленную внутрь объема;
– поправка, учитывающая уменьшение давления из-за взаимного притяжения молекул; силы взаимного притяжения молекул создают в тонком слое у стенки сосуда равнодействующую силу, направленную внутрь объема;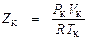 , и величина R взята по идеальному газу, т.е.
, и величина R взята по идеальному газу, т.е. 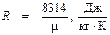 .
.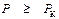 .
.
 (9.2)
(9.2) (9.3)
(9.3)
 ;
; 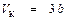 ;
;  . (9.7)
. (9.7)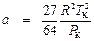 ;
;  ;
;  . (9.8)
. (9.8) .
. , в то время, как по идеальному газу
, в то время, как по идеальному газу .
. , (9.9)
, (9.9) ) получается для всех веществ одинаковым и равным 3/8 = 0,375, т.е. заметно отличается от разнообразных значений Z К в табл. 9.1, полученных для различных веществ.
) получается для всех веществ одинаковым и равным 3/8 = 0,375, т.е. заметно отличается от разнообразных значений Z К в табл. 9.1, полученных для различных веществ.


