
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения о дросселированииСодержание книги Поиск на нашем сайте
Дросселирование Методическое пособие к дисциплинам «Техническая термодинамика» и «Теоретические основы теплотехники» для студентов специальностей 270109 «теплогазоснабжение и вентиляция» и 140104 «промышленная теплоэнергетика»
Ижевск Издательство ИжГТУ УДК 621.1 ББК 31.31
Р ___
Составитель: д. техн. наук, проф. В. Н. Диденко
Рецензент: д. техн. наук, проф. В. Г. Исаков
Рекомендовано к изданию на заседании кафедры «Теплогенерирующие установки и газоснабжение» ИжГТУ «___» ____________ 2008 г.
В методическом пособии подробно рассматривается процесс дросселирования жидкостей, газов и паров. Раздел «Дросселирование» относится к разряду наиболее сложных в курсах «Техническая термодинамика» и «Теоретические основы теплотехники» и недостаточно раскрыт в учебной литературе. Материал раздела базируется на дисциплине «Термодинамика» (спецкурс). Сведения о фазовых переходах, необходимые для понимания материала, изложены автором в методических пособиях «Фазовые переходы» (Ижевск, 2003 г.) и «Водяной пар и его свойства» (Ижевск, 2007 г.). Автор выражает искреннюю благодарность Варфоломеевой Т.И. за помощь в подготовке данного пособия к изданию.
Настоящее методическое пособие предназначено для студентов специальностей 270109 «Теплогазоснабжение и вентиляция» и 140104 «Промышленная теплоэнергетика», магистрантов и аспирантов.
УДК 621.1 ББК 31.31
© Диденко В. Н., составление, 2008
© Ижевский государственный технический университет, 2008 Предисловие
Процесс дросселирования газов, паров и жидкостей широко применяется в различных механических устройствах. Изучение процесса дросселирования входит в рабочие программы таких учебных дисциплин как «Техническая термодинамика» и «Теоретические основы теплотехники». Как показывает практика, раздел «Дросселирование газов и паров» относится к одному из наиболее сложных для изучения студентами. В современных учебниках по технической термодинамике процесс дросселирования излагается достаточно поверхностно, без удовлетворительного физического и математического обоснования. Как правило, это однотипные клише, плохо раскрывающие суть процесса. Причинами такого положения являются прежде всего сложность термодинамического обоснования основных положений о процессе дросселирования и ограничения на объемы учебников. Авторы учебников обходят вопросы дросселирования насыщенных жидкостей, не объясняют физическую природу двух точек инверсии для заданного начального давления дросселирования, не раскрывают построение инверсионной кривой, приводят не все основные формулы, не дают вывод этих формул. Автор данного пособия систематизировал имеющийся материал о процессах дросселирования, обращая внимание на их физическое толкование и обоснование с помощью аппарата термодинамики. Автором предложены свои варианты вывода основных формул для процесса дросселирования, представленные в приложении.
Дросселирование пара
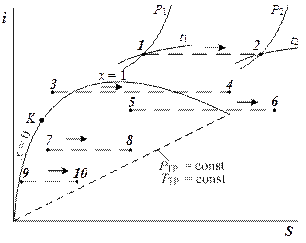
Пар по своим свойствам отличается от идеального газа, поэтому при дросселировании его температура в общем случае изменяется. Для анализа процесса дросселирования пара удобно использовать его i-S диаграмму (рис. 3.1).
Рис. 3.1. Процесс дросселирования пара в i-S диаграмме.
Перегретый пар в процессе дросселирования 1 – 2 остается перегретым. Перегретый пар в процессе 3 – 4 становится сначала сухим, затем влажным насыщенным, далее снова сухим и затем перегретым. Влажный насыщенный пар в процессе дросселирования 5 – 6 становится сначала сухим, а затем перегретым. Влажный насыщенный пар в процессе дросселирования 7 – 8 остается влажным насыщенным, изменяя кроме Р и Т еще и степень сухости. Кипящая насыщенная жидкость в процессе дросселирования 9 – 10 становится влажным насыщенным паром. Именно этот вариант дросселирования реализуется в парокомпрессорных холодильных установках.
Инверсионная кривая
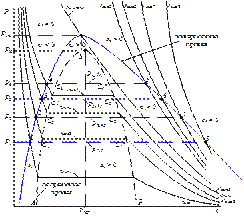
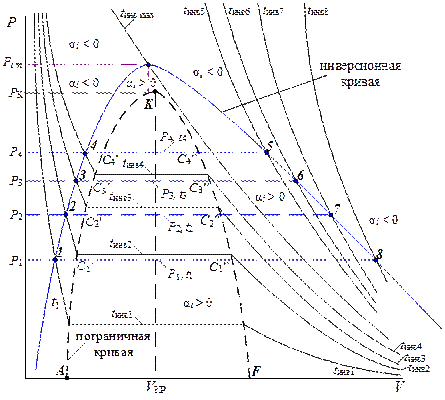
Геометрическое место точек инверсии называется инверсионной кривой. Инверсионная кривая – это совокупность левой и правой инверсионных кривых. На левой инверсионной кривой лежат все нижние точки инверсии, а на правой – все верхние. Построение инверсионной кривой в P-V координатах иллюстрируется рис. 8.1. Как следует из рис. 8.1. инверсионная кривая огибает пограничную кривую. Внутри инверсионной кривой α i > 0, т.е. дросселирование вызывает уменьшение температуры, а вне (α i < 0) – увеличение температуры рабочего тела.
Рис. 8.1. Построение инверсионной кривой в Р-V координатах
Из рис. 8.1. так же следует, что при давлении ниже критического Р К нижние точки инверсии соответствуют дросселированию жидкости, так как находятся левее нижней пограничной кривой вещества (х = 0). Верхние точки инверсии располагаются правее верхней пограничной кривой (х = 1) и поэтому соответствуют дросселированию газа. Как известно, пар – это газообразное состояние вещества при температуре ниже критической. Критическая изотерма, как видно из рис. 8.1, располагается внутри инверсионной кривой, поэтому вся область перегретого пара находится внутри инверсионной кривой, где α i > 0. Таким образом, при адиабатном дросселировании перегретый пар охлаждается. Инверсионную кривую обычно представляют в Р-Т координатах (рис. 8.2). При начальном давлении дросселирования
Рис. 8.2. Инверсионная кривая для азота
Для того, чтобы получить эффект охлаждения, необходимо так понизить начальную температуру t 1, чтобы точка с координатами (Р 1, t 1) оказались внутри инверсионной кривой. При Для получения уравнения инверсионной кривой в явном виде необходимо знать уравнение состояния данного вещества и использовать его в формулах (4.4) или (4.5) при α i = 0:
или
Уравнения (8.1) и (8.2) называются уравнениями инверсионной кривой. Если продифференцировать (8.1), полагая Р и V функциями температуры, то можно получить еще одно уравнение инверсионной кривой в общем виде:
Подробный вывод этого уравнения в варианте автора данного пособия дается в приложении (П.2). В точке максимума на инверсионной кривой (рис. 8.2)
Так как Т ≠ 0, то окончательно условие максимума инверсионной кривой приобретает следующий вид:
Для того, чтобы записать это уравнение в явном виде, необходимо знать конкретный вид уравнения состояния реального газа (Ван-дер-Ваальса, Дюпре и др.).
Приложение
П.1. Вывод формулы для дифференциального дроссель-эффекта (вариант автора пособия)
а) Определим тогда
откуда
б) Определим тогда
откуда
в) После подстановки (П1.2) и (П1.3) в уравнение (П1.1) имеем:
г) Определим откуда:
Определим то:
По третьему типу дифференциальных соотношений термодинамики
Тогда
Подставим (П1.6) в уравнение (П1.5):
д) Определим
Из общей термодинамики известно, что Тогда
Общая формула для теплоемкостей однородных систем, как известно из общей термодинамик, имеет вид:
Для изобарного процесса из этой формулы следует:
Подставим (П1.9) в (П1.8):
и
е) Подставим П(1.10) и (П1.7) в формулу (П1.4):
Выразим произведение
Тогда окончательно
П.2. Вывод формулы для инверсионной кривой (вариант автора пособия)
Продифференцируем уравнение (8.1):
Но удельный объем V является функцией Р и Т, поэтому
В соответствии с правилом нахождения полного дифференциала функции двух переменных запишем:
и окончательно
П.3. Вывод приближенной формулы для дифференциального дроссель-эффекта (вариант автора пособия)
Формулу (9.11) можно представить в другом виде, если подставить туда значение Р из уравнения (9.9):
Умножив числитель и знаменатель на (V – b), получим:
Подставим (П3.1) в формулу (4.4):
Окончательно
Как показывает численный анализ, при V >> b, слагаемыми, содержащими в знаменателе уравнения (П3.2) V во второй степени и выше, можно пренебречь. Тогда:
и окончательно:
Список литературы
1. Тепломеханика / В. Н. Луканин, М. Г. Шатров, Г. М. Камфер и др.; Под ред. В.Н. Луканина. – М.: Высшая школа, 1999. – 671 с. 2. Вукалович, М. П. Термодинамика / М. П. Вукалович, И. И. Новиков. – М.: Машиностроение, 1972. – 672 с. 3. Зубарев, В.Н. Практикум по технической термодинамике /В. Н. Зубарев, А. А. Александров, В. С. Охотин. – М.: Энергоатомиздат, 1986. – 304 с. Содержание
Предисловие. 3 1. Общие сведения о дросселировании. 3 2. Дросселирование идеального газа. 7 3. Дросселирование пара. 8 4. Дроссель-эффект Джоуля-Томсона. 9 4.1. Молекулярно-кинетическая природа изменения температуры газа в процессе дросселирования 10 4.2. Общие формулы для дифференциального дроссель-эффекта. 12 5. Дифференциальный дроссель-эффект в области двухфазных состояний вещества 15 6. Дифференциальный дроссель-эффект в критической точке. 18 7. Дифференциальный дроссель-эффект в однофазных областях. Точки инверсии. 19 8. Инверсионная кривая. 22 9. Дросселирование рабочего тела, подчиняющегося уравнению Ван-дер-Ваальса 25 9.1. Основные сведения об уравнении Ван-дер-Ваальса. 25 9.2. Качественный анализ процесса дросселирования с помощью уравнения Ван-дер-Ваальса 29 9.2.1. Построение инверсионной кривой. 29 9.3. Расчетное определение термодинамических параметров в точке максимума инверсионной кривой 33 9.4. Расчетное определение максимальной и минимальной температуры инверсии 36 10. Сравнение дроссель-эффекта с температурным эффектом адиабатного расширения 39 Приложение. 42 П.1. Вывод формулы для дифференциального дроссель-эффекта (вариант автора пособия) 42 П.2. Вывод формулы для инверсионной кривой (вариант автора пособия) 45 П.3. Вывод приближенной формулы для дифференциального дроссель-эффекта (вариант автора пособия) 46 Список литературы.. 49
Учебное издание
Составители: Диденко Валерий Николаевич
В редакции составителя
Подписано в печать. Формат 60×84/16. Усл. печ. л. Тираж ____ экз. Заказ № ___
Отпечатано в типографии Издательства ИжГТУ Издательство и типография Ижевского государственного технического университета. 426069, Ижевск, ул. Студенческая, 7 Дросселирование Методическое пособие к дисциплинам «Техническая термодинамика» и «Теоретические основы теплотехники» для студентов специальностей 270109 «теплогазоснабжение и вентиляция» и 140104 «промышленная теплоэнергетика»
Ижевск Издательство ИжГТУ УДК 621.1 ББК 31.31
Р ___
Составитель: д. техн. наук, проф. В. Н. Диденко
Рецензент: д. техн. наук, проф. В. Г. Исаков
Рекомендовано к изданию на заседании кафедры «Теплогенерирующие установки и газоснабжение» ИжГТУ «___» ____________ 2008 г.
В методическом пособии подробно рассматривается процесс дросселирования жидкостей, газов и паров. Раздел «Дросселирование» относится к разряду наиболее сложных в курсах «Техническая термодинамика» и «Теоретические основы теплотехники» и недостаточно раскрыт в учебной литературе. Материал раздела базируется на дисциплине «Термодинамика» (спецкурс). Сведения о фазовых переходах, необходимые для понимания материала, изложены автором в методических пособиях «Фазовые переходы» (Ижевск, 2003 г.) и «Водяной пар и его свойства» (Ижевск, 2007 г.). Автор выражает искреннюю благодарность Варфоломеевой Т.И. за помощь в подготовке данного пособия к изданию.
Настоящее методическое пособие предназначено для студентов специальностей 270109 «Теплогазоснабжение и вентиляция» и 140104 «Промышленная теплоэнергетика», магистрантов и аспирантов.
УДК 621.1 ББК 31.31
© Диденко В. Н., составление, 2008
© Ижевский государственный технический университет, 2008 Предисловие
Процесс дросселирования газов, паров и жидкостей широко применяется в различных механических устройствах. Изучение процесса дросселирования входит в рабочие программы таких учебных дисциплин как «Техническая термодинамика» и «Теоретические основы теплотехники». Как показывает практика, раздел «Дросселирование газов и паров» относится к одному из наиболее сложных для изучения студентами. В современных учебниках по технической термодинамике процесс дросселирования излагается достаточно поверхностно, без удовлетворительного физического и математического обоснования. Как правило, это однотипные клише, плохо раскрывающие суть процесса. Причинами такого положения являются прежде всего сложность термодинамического обоснования основных положений о процессе дросселирования и ограничения на объемы учебников. Авторы учебников обходят вопросы дросселирования насыщенных жидкостей, не объясняют физическую природу двух точек инверсии для заданного начального давления дросселирования, не раскрывают построение инверсионной кривой, приводят не все основные формулы, не дают вывод этих формул. Автор данного пособия систематизировал имеющийся материал о процессах дросселирования, обращая внимание на их физическое толкование и обоснование с помощью аппарата термодинамики. Автором предложены свои варианты вывода основных формул для процесса дросселирования, представленные в приложении.
Общие сведения о дросселировании
Дросселирование (мятие, редуцирование, торможение) – это явление уменьшения давления жидкости, пара или газа при внешне адиабатическом (без отвода или подвода теплоты) прохождении потоком местного сопротивления, уменьшающего проходное сечение. К таким местным сопротивлениям относятся диафрагмы, пористые перегородки (пробки), краны, вентили, задвижки, клапаны, капиллярные трубки и т.д. При дросселировании внешняя работа не совершается, есть только работа внутренних сил трения, приводящая к потере (диссипации) энергии потока и, как следствие, к понижению давления в струе газа или пара. Иногда дросселирование специально включают в рабочие процессы машин или систем, например: − для регулирования мощности паровых турбин за счет мятия пара перед входом в турбину; − для регулирования мощности карбюраторных двигателей внутреннего сгорания за счет изменения положения дроссельной заслонки карбюратора; − для понижения давления в редукционных клапанах систем тепло- и парогазоснабжения; − для понижения давления хладагентов в парокомпрессорных и абсорбционных холодильных установках; − для понижения давления в приборах, измеряющих расход газа. Первое начало термодинамики для газового потока в общем случае имеет следующий вид:
Здесь q – теплота, отнесенная к 1 кг системы; i – удельная энтальпия: w – средняя (расходная) скорость потока в рассматриваемом сечении; А ТЕХН – техническая работа, отнесенная к 1 кг системы.
Это уравнение справедливо как для обратимых, так и для необратимых процессов. Действие сил трения, а также вихревые движения за сужением потока делают процесс дросселирования необратимым. На преодоление сил трения затрачивается работа трения dА тр, которая полностью переходит в теплоту dq тр. Так как dA тр = dQ тр, то эти величины в уравнении первого начала термодинамики взаимно сокращаются. Тогда для внешне адиабатного потока (dq = 0), не совершающего к тому же технической работы (dА ТЕХН = 0), уравнение первого начала термодинамики приобретает следующий вид:
В интегральной форме уравнение (1.3) записывается следующим образом:
Схема процесса дросселирования представлена на рис. 1.1.
Рис. 1.1. Схема процесса дросселирования.
Как известно, при стационарном процессе течения рабочего тела его массовый расход G = const. В этом случае уравнение неразрывности имеет вид:
где F – площадь поперечного сечения канала; ρ – плотность рабочего тела; V – удельный объем рабочего тела:
При непрерывной площади поперечного сечения канала (F = const) из уравнения неразрывности следует:
Таким образом, скорость рабочего тела возрастает пропорционально увеличению его удельного объема. Как показывают количественные оценки, при таком изменении w и V величина изменения удельной кинетической энергии
в типичных случаях ничтожно мала по сравнению со значениями энтальпии i 1 и i 2. Тогда при
Это уравнение называется уравнением процесса дросселирования. В качестве примера рассмотрим дросселирование перегретого водяного пара с начальными параметрами Р 1 = 2,0 МПа, Т 1 = 810 °К и i 1 = 3550 кДж/кг до Р 2 = 0,2 МПа. При i 2 = i 1 = 3550 кДж/кг c помощью i-S диаграммы водяного пара определяем Т 2 = 800 °К и значения удельного объема пара до и после дросселирования: V 1 = 0,2 м3/кг, V 2 = 2,0 м3/кг. Так как при F = const и w / V = const, то увеличение V в 10 раз должно привести к увеличению w также в 10 раз. Пусть w 1 = 20 м/с, тогда w 2 = 200 м/с и приращение кинетической энергии потока будет равно
что составляет 0,56% от величины i 2. Из уравнения (1.3)
и для рассмотренного примера получаем i 1 = (1 + 0,0056) i 2. Таким образом, изменением кинетической энергии потока при дросселировании в этих случаях можно пренебречь и полагать
i 1 = i 2.
Но процесс дросселирования нельзя считать изоэнтальпийным. Как указывалось выше, в месте сужения потока скорость потока возрастает, а давление падает до значения Р '. Это увеличение кинетической энергии потока с помощью диффузора можно было бы превратить в потенциальную энергию, подняв давление до первоначального значения Р 1. При отсутствии диффузора основная часть кинетической энергии переходит в теплоту из-за образования вихрей за местным сопротивлением. Эта теплота воспринимается потоком, его энтропия при этом возрастает, и поток не возвращается в первоначальное состояние по давлению и температуре. Таким образом, внешне адиабатный процесс дросселирования является по своей сути необратимым.
|
||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 878; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |

 с любой начальной температурой t 1, всегда α i < 0, т.е. дросселирование сопровождается нагреванием газа. При любом начальном давлении Р 1 с начальной температурой дросселирования
с любой начальной температурой t 1, всегда α i < 0, т.е. дросселирование сопровождается нагреванием газа. При любом начальном давлении Р 1 с начальной температурой дросселирования  дросселирование также всегда приводит к нагреванию газа (α i < 0).
дросселирование также всегда приводит к нагреванию газа (α i < 0).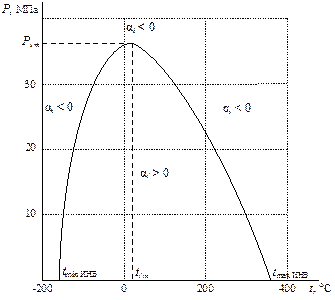
 дросселирование также приводит к нагреванию рабочего тела при любых значениях начального давления Р 1. В этом случае, для того, чтобы получить эффект охлаждения, необходимо так повысить начальную температуру t 1, чтобы точка с координатами (Р 1, t 1) оказалась внутри инверсионной кривой. Таким образом, дросселирование приводит к охлаждению рабочего тела (жидкости или пара) при всех сочетаниях термодинамических параметров состояния вещества перед дросселем (Р 1, t 1), соответствующих точкам внутри области, ограниченной сверху инверсионной кривой.
дросселирование также приводит к нагреванию рабочего тела при любых значениях начального давления Р 1. В этом случае, для того, чтобы получить эффект охлаждения, необходимо так повысить начальную температуру t 1, чтобы точка с координатами (Р 1, t 1) оказалась внутри инверсионной кривой. Таким образом, дросселирование приводит к охлаждению рабочего тела (жидкости или пара) при всех сочетаниях термодинамических параметров состояния вещества перед дросселем (Р 1, t 1), соответствующих точкам внутри области, ограниченной сверху инверсионной кривой.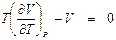 (8.1)
(8.1)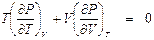 . (8.2)
. (8.2)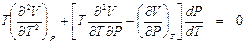 . (8.3)
. (8.3)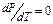 , поэтому для выполнения равенства (8.3) необходимо, чтобы
, поэтому для выполнения равенства (8.3) необходимо, чтобы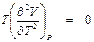 .
.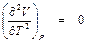 . (8.4)
. (8.4)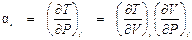 . (П1.1)
. (П1.1)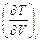 для формулы (П1.1). Пусть i = i (T, V),
для формулы (П1.1). Пусть i = i (T, V),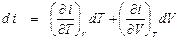 ,
,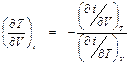 . (П1.2)
. (П1.2)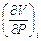 . Пусть i = i (Р, V),
. Пусть i = i (Р, V),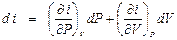 ,
,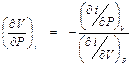 . (П1.3)
. (П1.3)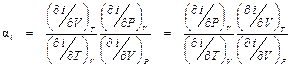 ,
,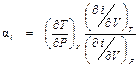 . (П1.4)
. (П1.4)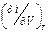 . Так как i = U + PV, то di =dU + PdV + VdP,
. Так как i = U + PV, то di =dU + PdV + VdP,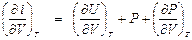 . (П1.5)
. (П1.5)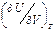 . Так как dU = ТdS – PdV,
. Так как dU = ТdS – PdV, .
. .
.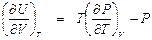 . (П1.6)
. (П1.6)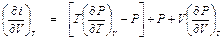 ,
,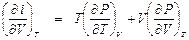 . (П1.7)
. (П1.7)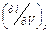 для формулы (П1.4). Представим эту производную в виде произведения двух частных производных:
для формулы (П1.4). Представим эту производную в виде произведения двух частных производных: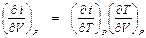 .
.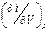 = СР.
= СР.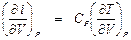 . (П1.8)
. (П1.8)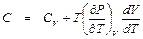 .
.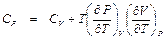 . (П1.9)
. (П1.9)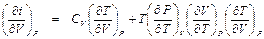
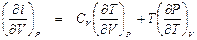 . (П1.10)
. (П1.10)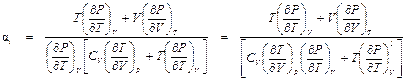 .
.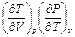 в знаменателе через произведение других частных производных, используя дифференциальные соотношения термодинамики:
в знаменателе через произведение других частных производных, используя дифференциальные соотношения термодинамики: . (П1.11)
. (П1.11)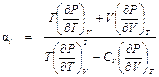 . (П1.12)
. (П1.12)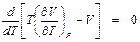 .
.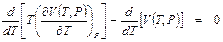 .
.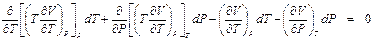 ,
,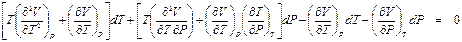 ,
,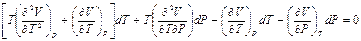 ,
,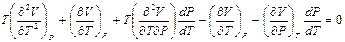
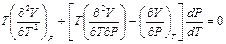 . (П2.1)
. (П2.1)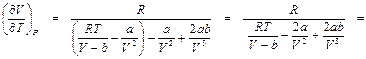
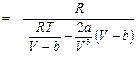 .
.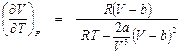 . (П3.1)
. (П3.1)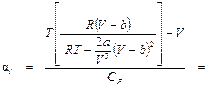
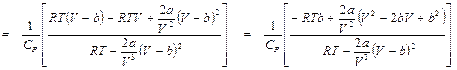 .
.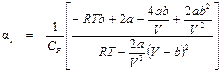 . (П3.2)
. (П3.2)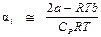
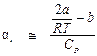 . (П3.3)
. (П3.3)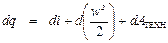 . (1.1)
. (1.1)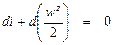 . (1.2)
. (1.2)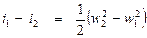 . (1.3)
. (1.3)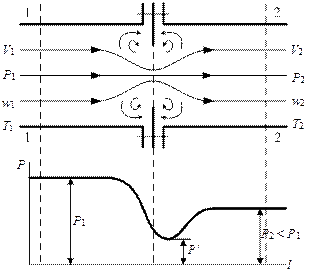
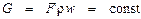 ,
,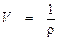 .
.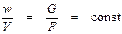 .
.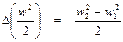
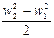 = 0 получаем:
= 0 получаем: . (1.4)
. (1.4)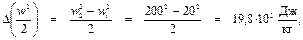
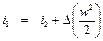 ,
,


