
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальный дроссель-эффект в критической точкеСодержание книги
Поиск на нашем сайте
В критической точке (точка К) как следует из рис. 5.1 Поэтому из формулы (4.5)
Таким образом, в критической точке для всех веществ дифференциальный дроссель-эффект (α i) равен обратной величине углового коэффициента кривой АК в точке К на Р-Т диаграмме. Как известно, в критической точке r К = 0 и
Эта неопределенность может быть раскрыта, но для этого должны быть известны зависимости r = r (T), Для нахождения
в которой производная
Дифференциальный дроссель-эффект в однофазных областях. Точки инверсии
Для анализа изменения α i в этих областях лучше всего воспользоваться первым уравнением (4.4):
Частная производная
откуда
Рис. 7.1. Изотермы в P-V диаграмме реального газа
Для газов повышение температуры при постоянном объеме всегда вызывает рост давления, т.е. Таким образом, для определения характера изменения в формуле (7.1) величины Как известно, частная производная Как следует из рис. 7.1. при P = const вне пограничной кривой AKF слева и справа от изохоры V КР = const, повышение температуры вызывает разное по знаку изменение Справа от прямой V КР = const в точках пересечения с изотермами t 4 = const, t 5 = const и t 6 = const (точки 4, 5 и 6 соответственно) угол наклона касательных к оси V возрастает по мере увеличения температуры. Слева от прямой V КР = const в точках пересечения изобары P = const с изотермами t 1 = const, t 2 = const и t 3 = const (точки 1, 2 и 3 соответственно) угловой коэффициент изотермы в этих точках (крутизна изотерм) наоборот убывает с повышением температуры. Таким образом, для любого значения P = const, не превышающего некоторое значение Pim > P K (см. следующий параграф) должны существовать две изотермы (обозначенные
Изотерма Числитель формулы (4.4) при этом становится равным нулю и дифференциальный дроссель-эффект α i в этих точках, нижней и верхней, также обращается в нуль. Дальнейший переход от «верхней» точки к изотермам с более высокими температурами (
Переход от «нижней» точки к изотермам с меньшими температурами ( Состояние, при котором α i меняет знак, называется точкой инверсии. Таким образом, точки, которые выше обозначались как «нижняя» и «верхняя», являются нижней и верхней инверсионными точками при заданном значении Р. При другом значении Р существуют две другие точки инверсии и т.д. Таким образом, множеству значений Р < Pim соответствует такое же множество пар точек инверсии.
Инверсионная кривая
Геометрическое место точек инверсии называется инверсионной кривой. Инверсионная кривая – это совокупность левой и правой инверсионных кривых. На левой инверсионной кривой лежат все нижние точки инверсии, а на правой – все верхние. Построение инверсионной кривой в P-V координатах иллюстрируется рис. 8.1. Как следует из рис. 8.1. инверсионная кривая огибает пограничную кривую. Внутри инверсионной кривой α i > 0, т.е. дросселирование вызывает уменьшение температуры, а вне (α i < 0) – увеличение температуры рабочего тела.
Рис. 8.1. Построение инверсионной кривой в Р-V координатах
Из рис. 8.1. так же следует, что при давлении ниже критического Р К нижние точки инверсии соответствуют дросселированию жидкости, так как находятся левее нижней пограничной кривой вещества (х = 0). Верхние точки инверсии располагаются правее верхней пограничной кривой (х = 1) и поэтому соответствуют дросселированию газа. Как известно, пар – это газообразное состояние вещества при температуре ниже критической. Критическая изотерма, как видно из рис. 8.1, располагается внутри инверсионной кривой, поэтому вся область перегретого пара находится внутри инверсионной кривой, где α i > 0. Таким образом, при адиабатном дросселировании перегретый пар охлаждается. Инверсионную кривую обычно представляют в Р-Т координатах (рис. 8.2). При начальном давлении дросселирования
Рис. 8.2. Инверсионная кривая для азота
Для того, чтобы получить эффект охлаждения, необходимо так понизить начальную температуру t 1, чтобы точка с координатами (Р 1, t 1) оказались внутри инверсионной кривой. При Для получения уравнения инверсионной кривой в явном виде необходимо знать уравнение состояния данного вещества и использовать его в формулах (4.4) или (4.5) при α i = 0:
или
Уравнения (8.1) и (8.2) называются уравнениями инверсионной кривой. Если продифференцировать (8.1), полагая Р и V функциями температуры, то можно получить еще одно уравнение инверсионной кривой в общем виде:
Подробный вывод этого уравнения в варианте автора данного пособия дается в приложении (П.2). В точке максимума на инверсионной кривой (рис. 8.2)
Так как Т ≠ 0, то окончательно условие максимума инверсионной кривой приобретает следующий вид:
Для того, чтобы записать это уравнение в явном виде, необходимо знать конкретный вид уравнения состояния реального газа (Ван-дер-Ваальса, Дюпре и др.).
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.22.184 (0.01 с.) |

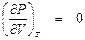 , а из рис. 5.2 –
, а из рис. 5.2 – 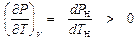 .
. . (6.1)
. (6.1) , поэтому
, поэтому .
. и
и 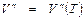 .
.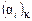 лучше всего воспользоваться формулой
лучше всего воспользоваться формулой ,
, в точке К определяется из уравнения состояния реального газа (Ван-дер-Ваальса, Дюпре, Вукаловича-Новикова и др.)
в точке К определяется из уравнения состояния реального газа (Ван-дер-Ваальса, Дюпре, Вукаловича-Новикова и др.)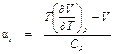 . (4.4)
. (4.4) определяется по формуле П1.11 (приложение П1):
определяется по формуле П1.11 (приложение П1): ,
, . (7.1)
. (7.1)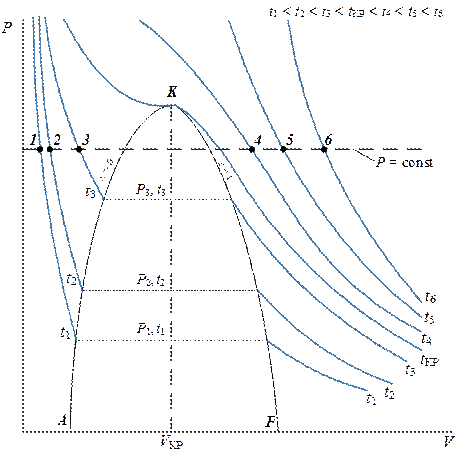
 .
.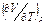 при изменении температуры в условиях P = const, необходимо знать характер изменения величины изотермической упругости
при изменении температуры в условиях P = const, необходимо знать характер изменения величины изотермической упругости 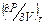 , которая всегда меньше нуля.
, которая всегда меньше нуля. – это угловой коэффициент кривой
– это угловой коэффициент кривой  при заданной температуре Т (в Р-V координатах это тангенс угла наклона к оси V касательной в данной точке к кривой P = P (V)).
при заданной температуре Т (в Р-V координатах это тангенс угла наклона к оси V касательной в данной точке к кривой P = P (V)). .
.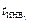 и
и  ), у которых в точках пересечения с изобарой P = const выполняется равенство:
), у которых в точках пересечения с изобарой P = const выполняется равенство: .
. расположена слева от изохоры V КР = const, а
расположена слева от изохоры V КР = const, а 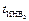 – справа.
– справа. ) приведет к тому, что будет выполняться неравенство
) приведет к тому, что будет выполняться неравенство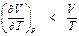 , то есть α i поменяет знак на отрицательный.
, то есть α i поменяет знак на отрицательный.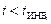 ) также приведет к выполнению неравенства
) также приведет к выполнению неравенства 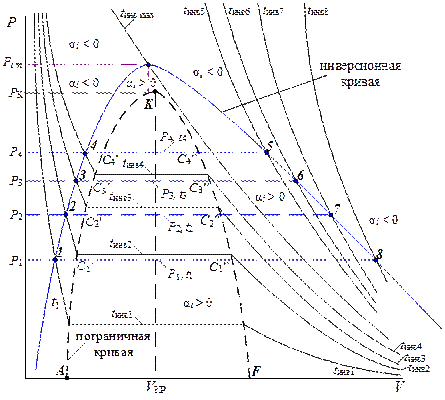
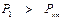 с любой начальной температурой t 1, всегда α i < 0, т.е. дросселирование сопровождается нагреванием газа. При любом начальном давлении Р 1 с начальной температурой дросселирования
с любой начальной температурой t 1, всегда α i < 0, т.е. дросселирование сопровождается нагреванием газа. При любом начальном давлении Р 1 с начальной температурой дросселирования 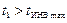 дросселирование также всегда приводит к нагреванию газа (α i < 0).
дросселирование также всегда приводит к нагреванию газа (α i < 0).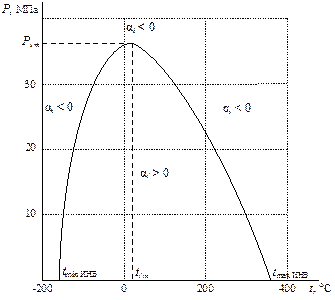
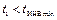 дросселирование также приводит к нагреванию рабочего тела при любых значениях начального давления Р 1. В этом случае, для того, чтобы получить эффект охлаждения, необходимо так повысить начальную температуру t 1, чтобы точка с координатами (Р 1, t 1) оказалась внутри инверсионной кривой. Таким образом, дросселирование приводит к охлаждению рабочего тела (жидкости или пара) при всех сочетаниях термодинамических параметров состояния вещества перед дросселем (Р 1, t 1), соответствующих точкам внутри области, ограниченной сверху инверсионной кривой.
дросселирование также приводит к нагреванию рабочего тела при любых значениях начального давления Р 1. В этом случае, для того, чтобы получить эффект охлаждения, необходимо так повысить начальную температуру t 1, чтобы точка с координатами (Р 1, t 1) оказалась внутри инверсионной кривой. Таким образом, дросселирование приводит к охлаждению рабочего тела (жидкости или пара) при всех сочетаниях термодинамических параметров состояния вещества перед дросселем (Р 1, t 1), соответствующих точкам внутри области, ограниченной сверху инверсионной кривой.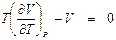 (8.1)
(8.1)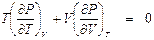 . (8.2)
. (8.2)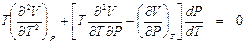 . (8.3)
. (8.3)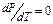 , поэтому для выполнения равенства (8.3) необходимо, чтобы
, поэтому для выполнения равенства (8.3) необходимо, чтобы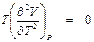 .
.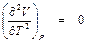 . (8.4)
. (8.4)


