
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение дроссель-эффекта с температурным эффектом адиабатного расширенияСодержание книги
Поиск на нашем сайте
Из курса общей термодинамики (раздел «Вычисление энтропии») известно соотношение:
Для обратимого адиабатного процесса (dS = 0) это уравнение приобретает следующий вид:
откуда следует
Обозначим температурный эффект обратимого адиабатного расширения как
Сравним α S с дроссель-эффектом α i (примечание: α i иногда называют температурным эффектом необратимого адиабатного процесса расширения).
Окончательно
Из уравнения (10.2) следует, что при адиабатном расширении газ охлаждается сильнее, чем при адиабатном дросселировании. Для получения низких температур, например, сжижение газов, целесообразно использовать детандеры – расширительные цилиндры, в которых производится адиабатное расширение газа. Как было показано выше, охлаждение рабочего тела при дросселировании (α i > 0), возможно лишь при расположении начальных точек дросселирования (Р 1, Т 1) в определенных областях, Так, например, при Т 1> Т ИНВ max охлаждение газа при дросселировании невозможно ни при каких значениях начального давления Р 1. В случае адиабатного расширения охлаждение рабочего тела (даже идеального газа) достигается всегда, при любом сочетании начальных значений термодинамических параметров (Р 1, Т 1). Последнее является большим достоинством метода охлаждения за счет адиабатного расширения. Недостатком этого метода является техническая сложность осуществления регулирования температуры охлаждения. Метод дросселирования свободен от этого недостатка, но приводит к некоторому снижению эффективности работы холодильной установки. Как следует из уравнения (10.2), в области двухфазных состояний вещества, где СР → ∞, α S = α i, т.е. одинаковый перепад давления Р 1 – Р 2, приводит к одинаковому понижению температуры Т 1 – Т 2. Чем больше реальный процесс адиабатного расширения газа в детандере отличается от обратимого действием сил трения, ведущих к нагреванию газа, тем сильнее α S стремится к α i. Процесс дросселирования из-за его необратимости приводит к снижению работоспособности газа (пара) по сравнению с адиабатным обратимым расширением. Рассмотрим два варианта расширения пара от P 1 до P 3:
Теоретическая работа пара при таком варианте расширения будет меньше и равна разности i 2 – i 4, где i 2 = i 1, а i 4 > i 3. Это иллюстрируется рис. 10.1
Рис. 10.1. Влияние процесса дросселирования на работоспособность пара
Потеря работоспособности 1 кг пара в приведенном примере составит:
Приложение
П.1. Вывод формулы для дифференциального дроссель-эффекта (вариант автора пособия)
а) Определим тогда
откуда
б) Определим тогда
откуда
в) После подстановки (П1.2) и (П1.3) в уравнение (П1.1) имеем:
г) Определим откуда:
Определим то:
По третьему типу дифференциальных соотношений термодинамики
Тогда
Подставим (П1.6) в уравнение (П1.5):
д) Определим
Из общей термодинамики известно, что Тогда
Общая формула для теплоемкостей однородных систем, как известно из общей термодинамик, имеет вид:
Для изобарного процесса из этой формулы следует:
Подставим (П1.9) в (П1.8):
и
е) Подставим П(1.10) и (П1.7) в формулу (П1.4):
Выразим произведение
Тогда окончательно
П.2. Вывод формулы для инверсионной кривой (вариант автора пособия)
Продифференцируем уравнение (8.1):
Но удельный объем V является функцией Р и Т, поэтому
В соответствии с правилом нахождения полного дифференциала функции двух переменных запишем:
и окончательно
П.3. Вывод приближенной формулы для дифференциального дроссель-эффекта (вариант автора пособия)
Формулу (9.11) можно представить в другом виде, если подставить туда значение Р из уравнения (9.9):
Умножив числитель и знаменатель на (V – b), получим:
Подставим (П3.1) в формулу (4.4):
Окончательно
Как показывает численный анализ, при V >> b, слагаемыми, содержащими в знаменателе уравнения (П3.2) V во второй степени и выше, можно пренебречь. Тогда:
и окончательно:
Список литературы
1. Тепломеханика / В. Н. Луканин, М. Г. Шатров, Г. М. Камфер и др.; Под ред. В.Н. Луканина. – М.: Высшая школа, 1999. – 671 с. 2. Вукалович, М. П. Термодинамика / М. П. Вукалович, И. И. Новиков. – М.: Машиностроение, 1972. – 672 с. 3. Зубарев, В.Н. Практикум по технической термодинамике /В. Н. Зубарев, А. А. Александров, В. С. Охотин. – М.: Энергоатомиздат, 1986. – 304 с. Содержание
Предисловие. 3 1. Общие сведения о дросселировании. 3 2. Дросселирование идеального газа. 7 3. Дросселирование пара. 8 4. Дроссель-эффект Джоуля-Томсона. 9 4.1. Молекулярно-кинетическая природа изменения температуры газа в процессе дросселирования 10 4.2. Общие формулы для дифференциального дроссель-эффекта. 12 5. Дифференциальный дроссель-эффект в области двухфазных состояний вещества 15 6. Дифференциальный дроссель-эффект в критической точке. 18 7. Дифференциальный дроссель-эффект в однофазных областях. Точки инверсии. 19 8. Инверсионная кривая. 22 9. Дросселирование рабочего тела, подчиняющегося уравнению Ван-дер-Ваальса 25 9.1. Основные сведения об уравнении Ван-дер-Ваальса. 25 9.2. Качественный анализ процесса дросселирования с помощью уравнения Ван-дер-Ваальса 29 9.2.1. Построение инверсионной кривой. 29 9.3. Расчетное определение термодинамических параметров в точке максимума инверсионной кривой 33 9.4. Расчетное определение максимальной и минимальной температуры инверсии 36 10. Сравнение дроссель-эффекта с температурным эффектом адиабатного расширения 39 Приложение. 42 П.1. Вывод формулы для дифференциального дроссель-эффекта (вариант автора пособия) 42 П.2. Вывод формулы для инверсионной кривой (вариант автора пособия) 45 П.3. Вывод приближенной формулы для дифференциального дроссель-эффекта (вариант автора пособия) 46 Список литературы.. 49
Учебное издание
Составители: Диденко Валерий Николаевич
В редакции составителя
Подписано в печать. Формат 60×84/16. Усл. печ. л. Тираж ____ экз. Заказ № ___
Отпечатано в типографии Издательства ИжГТУ Издательство и типография Ижевского государственного технического университета. 426069, Ижевск, ул. Студенческая, 7
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 591; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.95.197 (0.007 с.) |

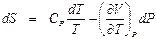 .
.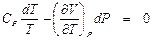 ,
,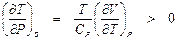 .
.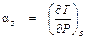 .
.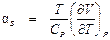 . (10.1)
. (10.1)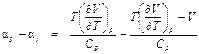 .
.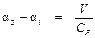 . (10.2)
. (10.2)
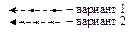
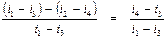 .
.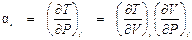 . (П1.1)
. (П1.1)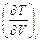 для формулы (П1.1). Пусть i = i (T, V),
для формулы (П1.1). Пусть i = i (T, V),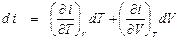 ,
,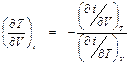 . (П1.2)
. (П1.2)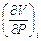 . Пусть i = i (Р, V),
. Пусть i = i (Р, V),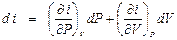 ,
,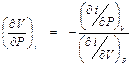 . (П1.3)
. (П1.3)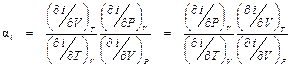 ,
,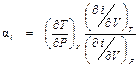 . (П1.4)
. (П1.4)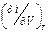 . Так как i = U + PV, то di =dU + PdV + VdP,
. Так как i = U + PV, то di =dU + PdV + VdP,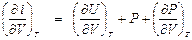 . (П1.5)
. (П1.5)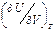 . Так как dU = ТdS – PdV,
. Так как dU = ТdS – PdV, .
. .
.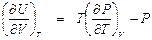 . (П1.6)
. (П1.6)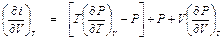 ,
,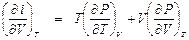 . (П1.7)
. (П1.7)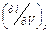 для формулы (П1.4). Представим эту производную в виде произведения двух частных производных:
для формулы (П1.4). Представим эту производную в виде произведения двух частных производных: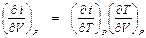 .
.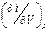 = СР.
= СР.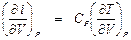 . (П1.8)
. (П1.8)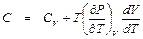 .
.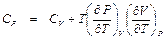 . (П1.9)
. (П1.9)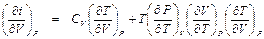
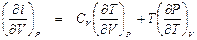 . (П1.10)
. (П1.10)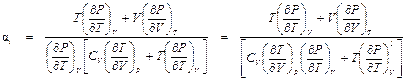 .
.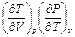 в знаменателе через произведение других частных производных, используя дифференциальные соотношения термодинамики:
в знаменателе через произведение других частных производных, используя дифференциальные соотношения термодинамики: . (П1.11)
. (П1.11)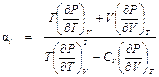 . (П1.12)
. (П1.12)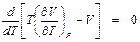 .
.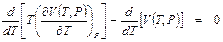 .
.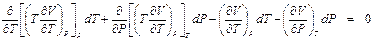 ,
,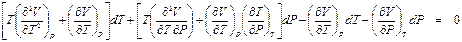 ,
,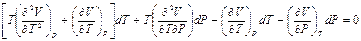 ,
,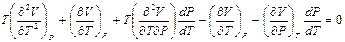
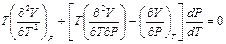 . (П2.1)
. (П2.1)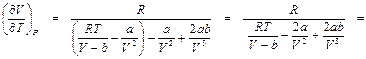
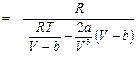 .
.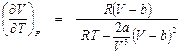 . (П3.1)
. (П3.1)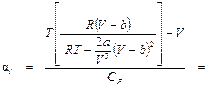
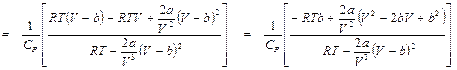 .
.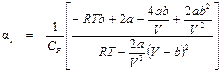 . (П3.2)
. (П3.2)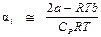
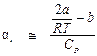 . (П3.3)
. (П3.3)


