
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отработка гармонических сигналовСодержание книги Поиск на нашем сайте
В программном пакете Matlab/simulink построим графики реакций системы по выходу усилителя мощности и выходу датчика обратной связи на гармонические сигналы с амплитудой 1В, 3В, 5В и частотой
Рисунок 64 – Модель для построения графиков реакций на входное гармоническое воздействие с учетом нелинейности
Реакция системы на входное гармоническое воздействие при амплитуде 1В (Рисунки 65, 66).
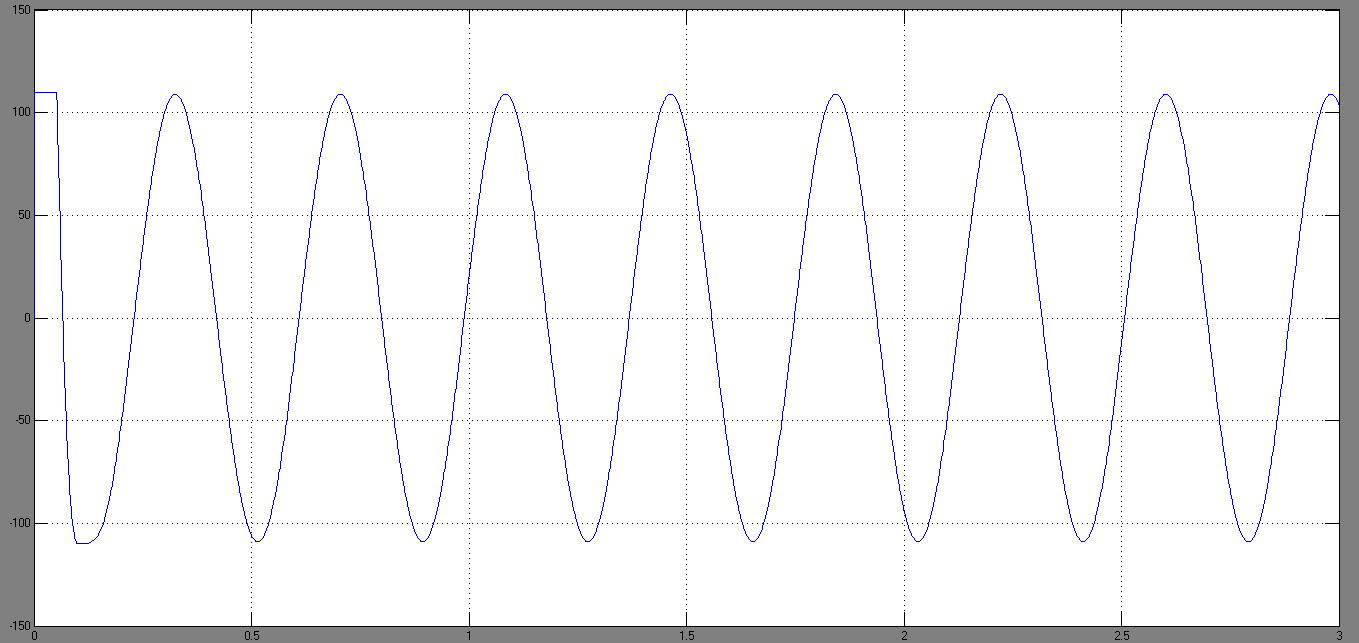
Рисунок 65 – Реакция системы на входное гармоническое воздействие амплитудой 1В по выходу ДОС
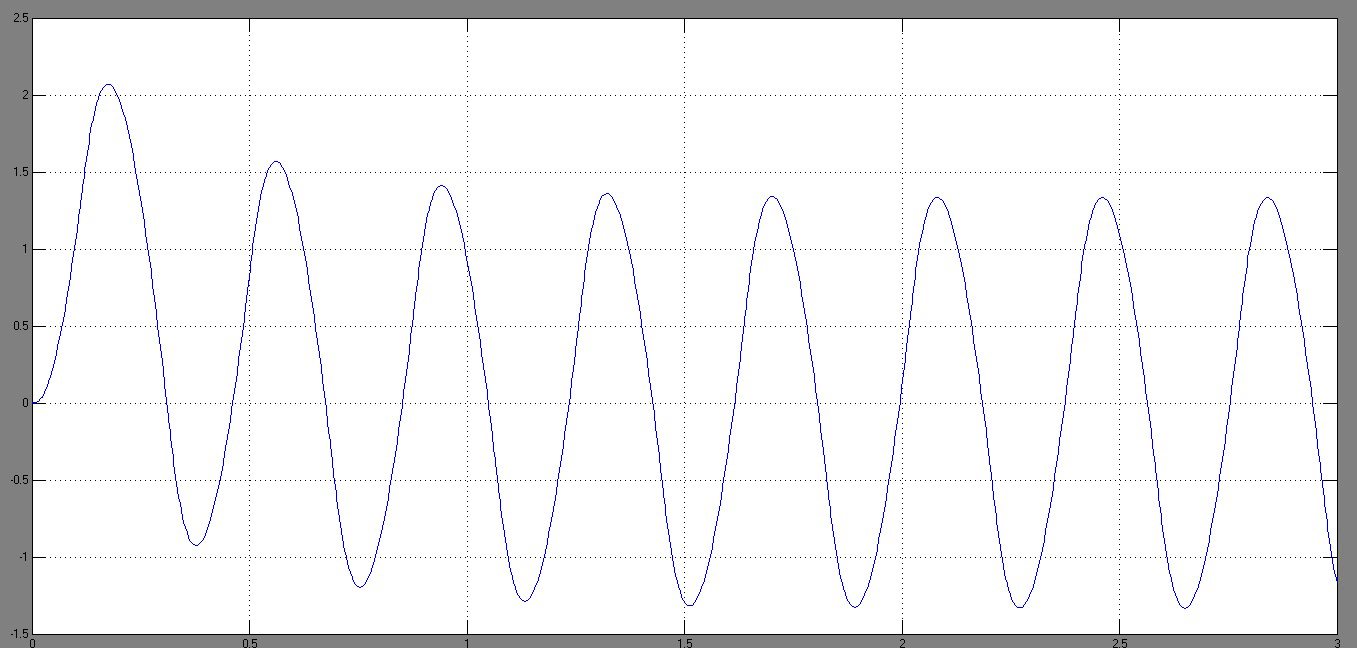
Рисунок 66 – Реакция системы на входное гармоническое воздействие амплитудой 1В по выходу УМ
Реакция системы на входное гармоническое воздействие при амплитуде 3В (Рисунки 67, 68).
Рисунок 67 – Реакция системы на входное гармоническое воздействие амплитудой 3В по выходу ДОС
Рисунок 68 – Реакция системы на входное гармоническое воздействие амплитудой 3В по выходу УМ
Реакция системы на входное гармоническое воздействие при амплитуде 5В (Рисунки 69, 70).
Рисунок 69 – Реакция системы на входное гармоническое воздействие амплитудой 5В по выходу ДОС
Рисунок 70 – Реакция системы на входное гармоническое воздействие амплитудой 5В по выходу УМ Определим амплитудно-фазовые искажения отработки входного сигнала. Построим графики входного и выходного сигнала в одной плоскости с помощью программного пакета Matlab в среде Simulink (рисунок 72). Используем модель, приведенную на рисунке 71.
Рисунок 71 – Модель для нахождения АФИ при отработке гармонического сигнала
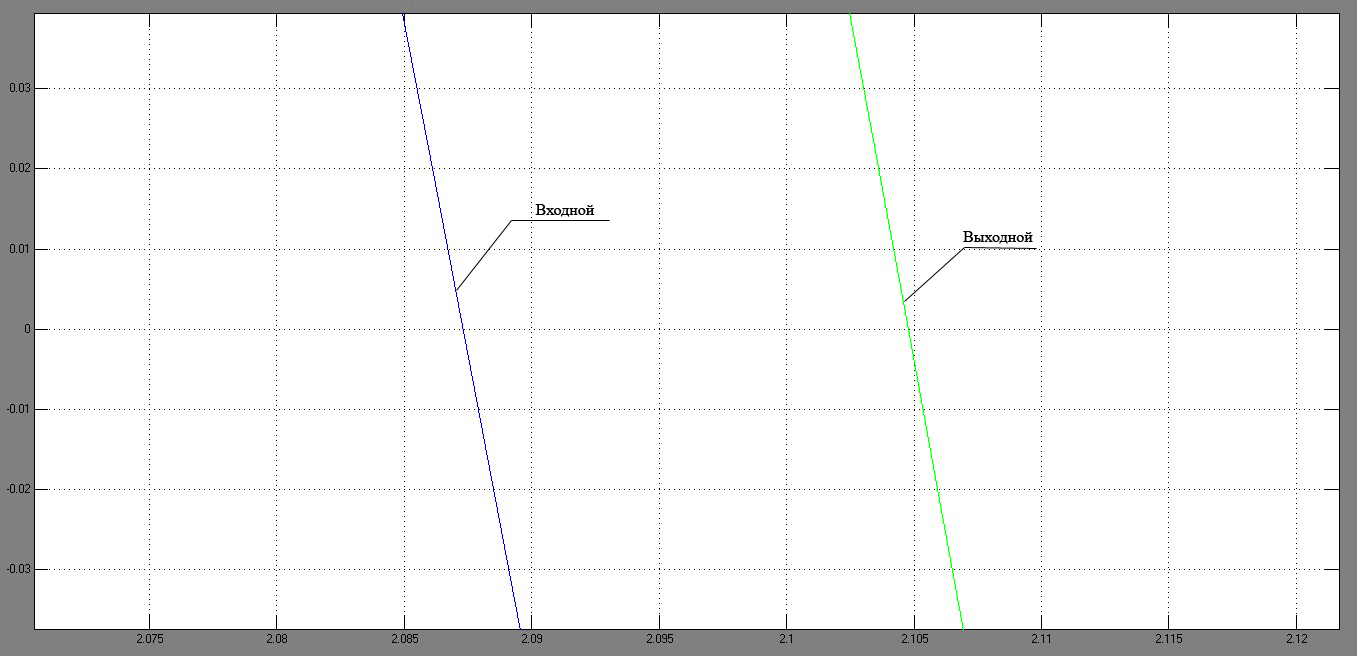
Рисунок 72 – Графики входного и выходного сигналов Для определения искажений по амплитуде и по фазе увеличим некоторые участки графиков (рисунки 73,74).
Рисунок 73 – Увеличенная часть графика для определения искажений по амплитуде
Рисунок 74 – Увеличенная часть графика для определения искажений по фазе Амплитудные искажения По рисунку 74 видно, что Тогда фазовые искажения Найденные амплитудно-фазовые искажения совпали с теми, которые мы нашли в пункте 3.3. Определение возможности возникновения автоколебаний в замкнутой системе. Определим возможность возникновения автоколебаний в замкнутой системе. В гармонически линеаризованной системе имеют место незатухающие колебания управляемой величины, если она находится на границе устойчивости, т.к. ее годограф Найквиста проходит через особую точку.
С помощью программного пакета MathCAD на комплексной плоскости построим АФЧХ линейного элемента и годограф инверсного эквивалентного комплексного коэффициент усиления (ЭККУ) (рисунок 75). При построении будем учитывать люфт в кинематической передаче. Величина люфта 11 угловых минут, что составляет примерно
Рисунок 75 – АФЧХ линейной части системы и годограф ЭККУ
В системе возможно возникновение периодического процесса, если АФЧХ линейной части системы и годограф ЭККУ имеют общие точки. Из рисунка 75 видно, что таких точек нет, значит, возникновение автоколебаний в системе невозможно.
Заключение В ходе выполнения курсовой работы было установлено, что исходная система не удовлетворяет требованиям технического задания. Для корректировки системы был проведен синтез регулятора, после чего характеристики системы значительно улучшились и стали соответствовать ТЗ. Затем был проведен расширенный анализ полученной СУ, который показал, что система устойчива (по критериям Найквиста и Михайлова). Были определены запасы устойчивости, а также характеристики системы в переходном и установившемся режиме. Также была исследована точность системы, рассчитаны и построены графики ошибок при отработке системой линейного и гармонического сигналов. Также был проведен анализ системы с учетом нелинейности усилителя мощности и люфта в кинематической передаче.
Библиографический список 1. Бесекерский, В.А.Теория систем автоматического регулирования / В.А. Бесекерский, Е.П. Попов. – 3-е изд. – Москва: Наука, 1975. – 767с. 2. Макаров, И.М. Линейные автоматические системы / И.М. Макаров, Б.М. Менский. – 2-е изд. – Москва: Машиностроение, 1982. – 504 с. 3. Павловская, О.О. Теория автоматического управления: учебное пособие к лабораторным и курсовым работам / О.О. Павловская, И.В. Чернецкая. – Челябинск: Издательский центр ЮУрГУ, 2010. – 93 с. 4. Долбенков, В.И. Simulink в задачах систем автоматического управления: учебное пособие / В.И. Долбенков. – Челябинск: Изд-во ЮУрГУ, 2005. – 101 с.
Приложение А. Исходная и желаемая ЛАЧХ
Приложение Б. Увеличенные графики реакций системы по выходу ДОС для пункта 5.1
Рисунок 76 – Увеличенный график реакции на
Рисунок 77 – Увеличенный график реакции на
Рисунок 78 – Увеличенный график реакции на
Рисунок 79 – Увеличенный график реакции на
Рисунок 80 – Увеличенный график реакции на
Рисунок 81 – Увеличенный график реакции на единичный сигнал для определения времени переходного процесса
Приложение В. Построение годографов в пункте 5.3 с помощью MathCAD
Рисунок 82 – МаthCAD-выкладки для построения годографов
Приложение Г. Математическое описание УМ и КС
Рисунок 83 – Зона насыщения усилителя мощности Математически усилитель мощности можно описать функцией:
В кинематической связи нашей системы проявляется люфт, который можно описать графически:
Рисунок 84 – Люфт
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 612; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.214.16 (0.009 с.) |

 рад/с. При построении графиков будем учитывать нелинейность усилителя мощности (модель на рисунке 64).
рад/с. При построении графиков будем учитывать нелинейность усилителя мощности (модель на рисунке 64).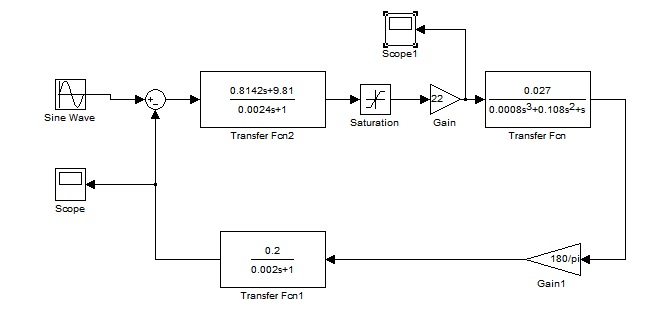







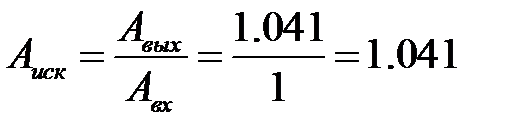 .
.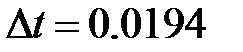 с.
с. град.
град. радиан. Необходимые для построения MathCAD-выкладки отображены в приложении В.
радиан. Необходимые для построения MathCAD-выкладки отображены в приложении В.

 для определения перерегулирования
для определения перерегулирования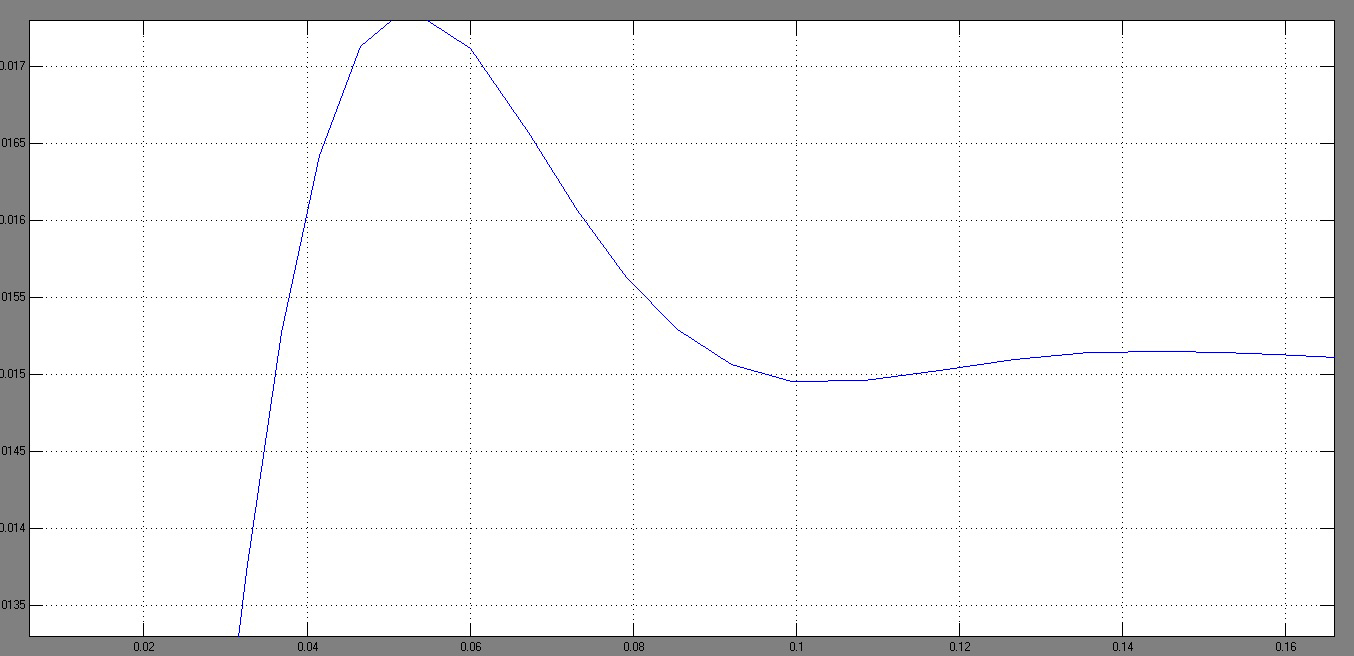

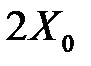 для определения перерегулирования
для определения перерегулирования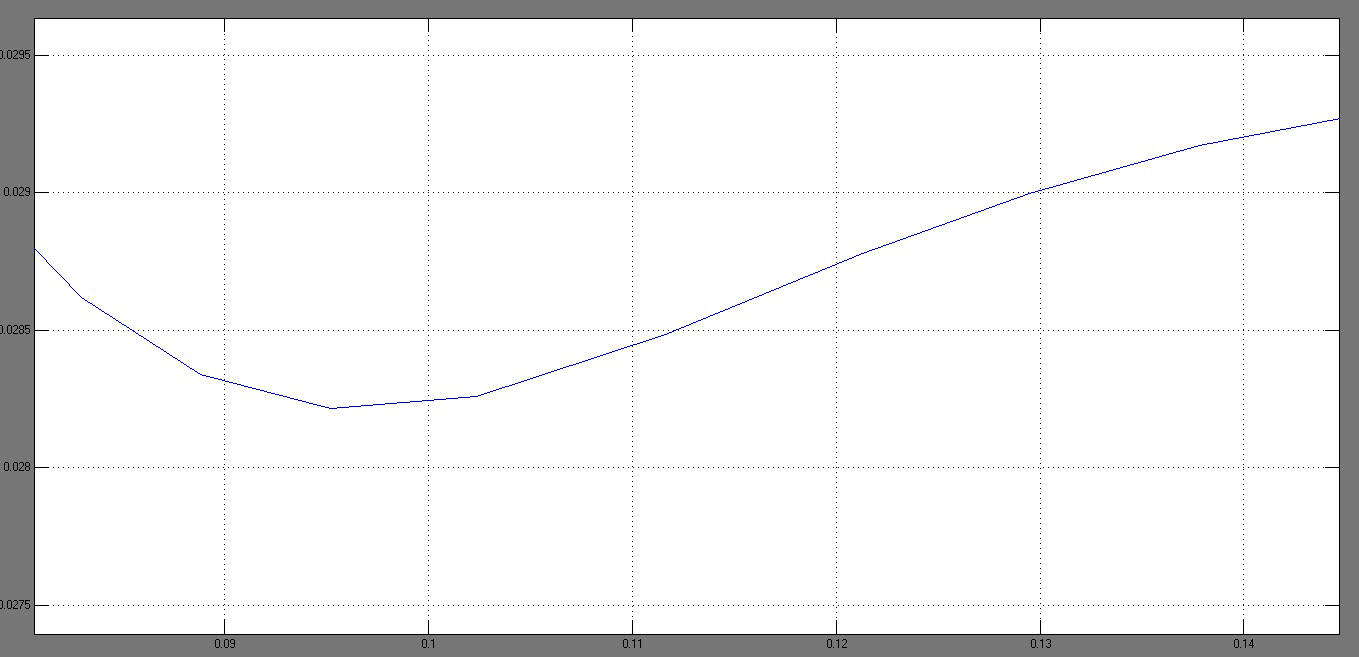
 для определения времени переходного процесса
для определения времени переходного процесса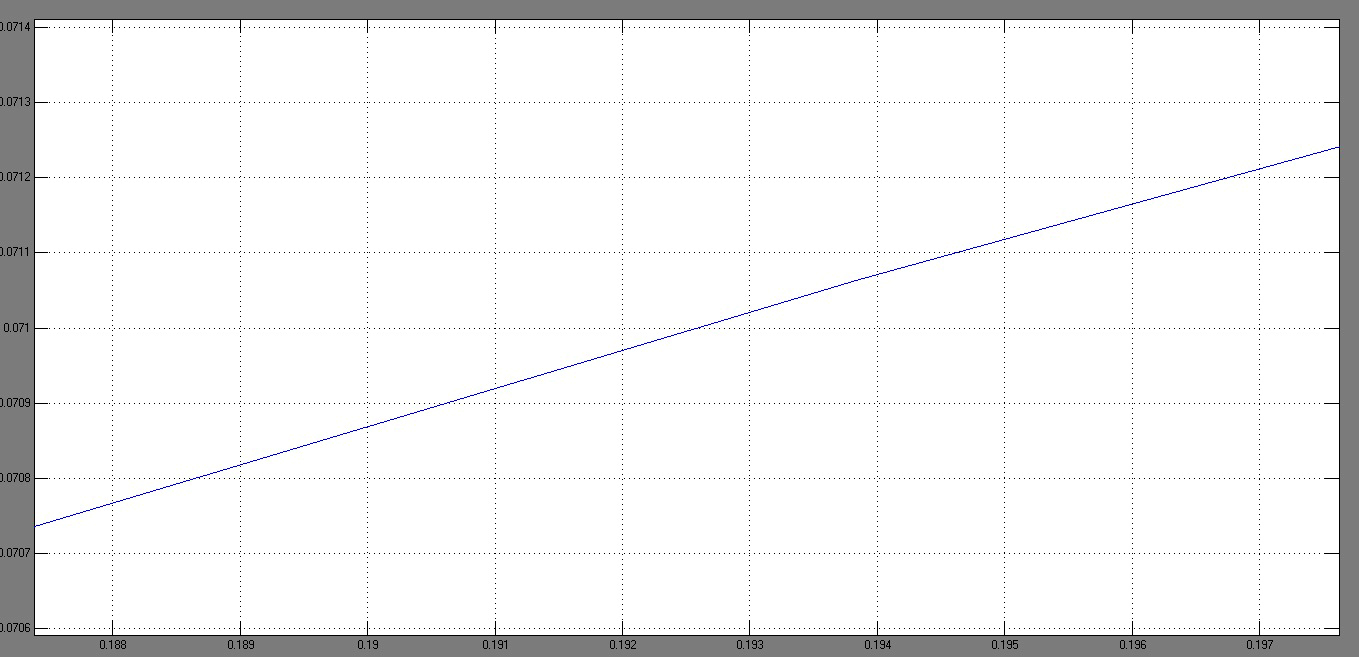
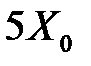 для определения времени переходного процесса
для определения времени переходного процесса







