
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ качества системы в установившемся режимеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Амплитудно-фазовые искажения в системе были найдены в пункте 2.5.2. Рассчитаем установившуюся ошибку для заданных в ТЗ сигналов. Для единичного ступенчатого сигнала
Значит установившаяся ошибка при единичном ступенчатом входном воздействии Установившуюся ошибку при линейно нарастающем входном воздействии найдем в пункте 3.2. Для того, чтобы определить установившуюся ошибку при гармоническом сигнале
Построим АЧХ по выходу усилителя мощности. Для этого перейдем к частотной передаточной функции и выделим ее модуль. Построение проведем в программном пакете MathCAD (рисунок 34). По графику определим, когда значение модуля равно 110 В.
Рисунок 34 – Нахождение частоты Из рисунка 34 видно, что
Ошибка при гармоническом входном воздействии тоже имеет гармонический вид
Отработка типовых входных сигналов. Единичный ступенчатый сигнал Построим переходные характеристики системы по выходу объекта управления, по выходу датчика обратной связи и по выходу усилителя мощности с помощью программного пакета matlab/simulink (рисунки 36, 37, 38). Для построения характеристик используется модель отображенная на рисунке 35.
Рисунок 35 – Модель системы в Simulink
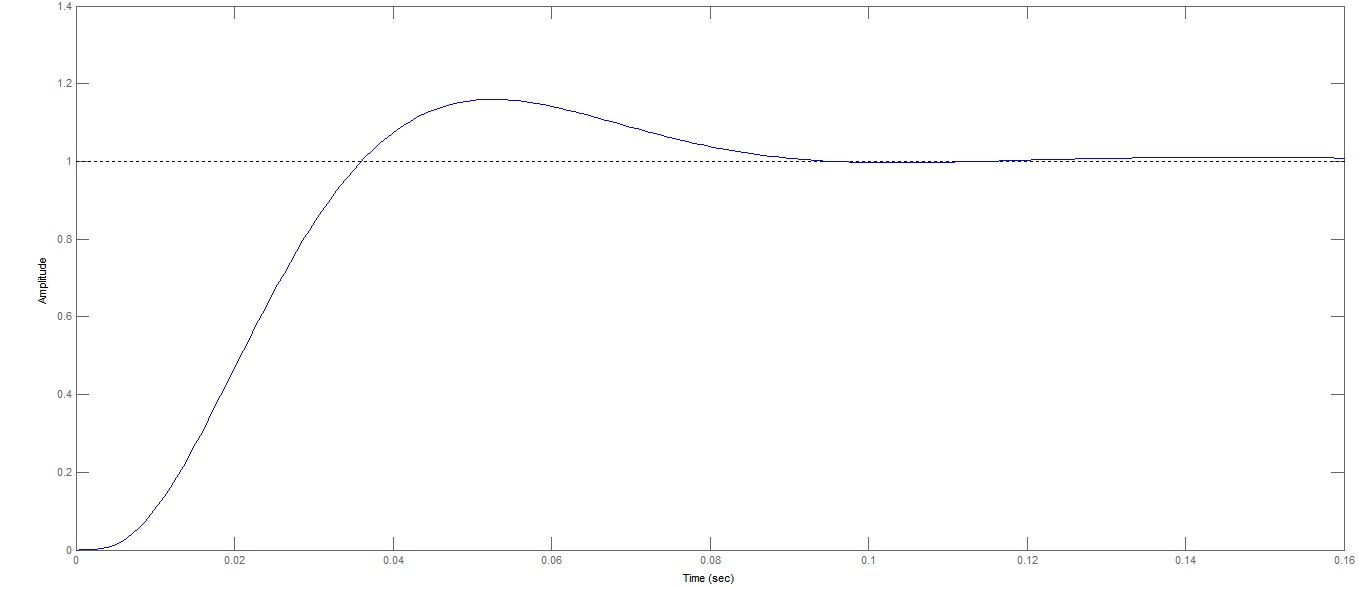
Рисунок 36 – Переходная характеристика по выходу ОУ
Рисунок 37 – Переходная характеристика по выходу ДОС
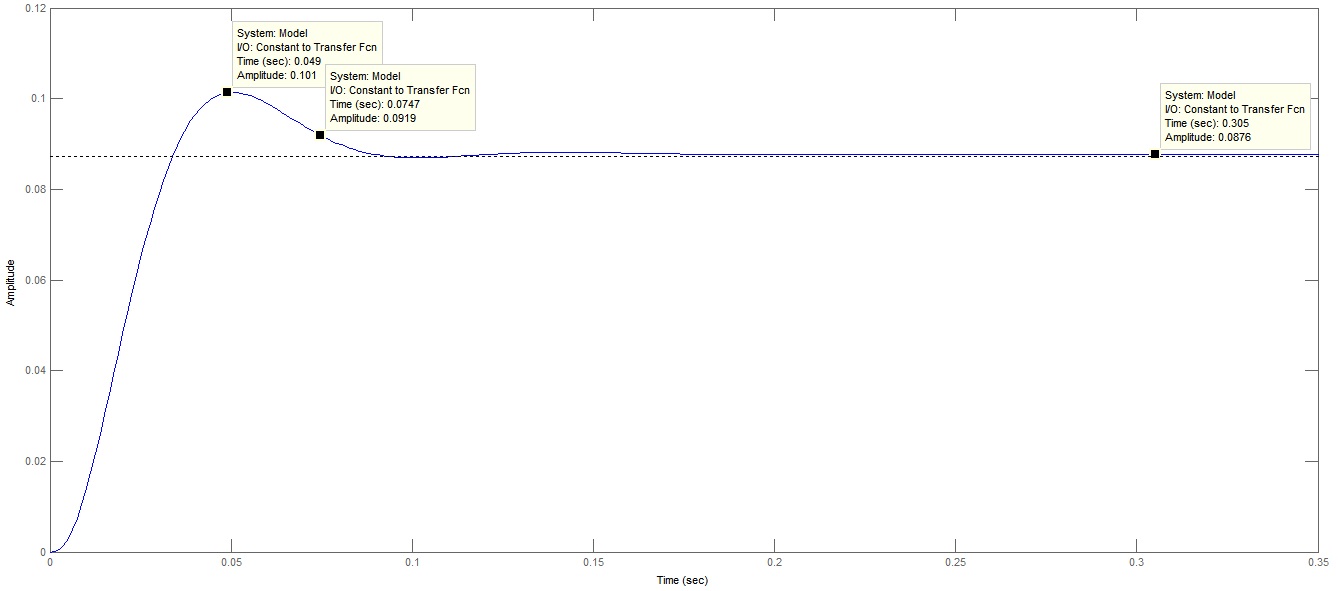
Рисунок 38 – Переходная характеристика по выходу УМ Определим прямые показатели качества переходного процесса по выходу ОУ. Необходимые параметры для определения показателей качества указаны на рисунке 35.
Прямые показатели качества переходного процесса по выходу ДОС были определены выше в пункте 2.5.2 – По графикам определим начальные и установившиеся значения:
Рассчитаем величину входного сигнала
Определим начальные и установившиеся значения реакций системы на ступенчатый сигнал величины
Рисунок 39 – Реакция на
Рисунок 40 – Реакция на
Рисунок 41 – Реакция на
По графикам определим начальные и установившиеся значения:
Сравнивая данные величины с величинами, полученными ранее при единичном входящем воздействии, можно заметить, что из-за уменьшения величины сигнала, значения реакций тоже уменьшились. Сигнал с постоянной скоростью Рассчитаем коэффициенты ошибок системы.
Определим установившуюся ошибку при линейно нарастающем входном сигнале.
Коэффициент
Рисунок 42 – Нахождение коэффициента Из рисунка 41 видно, что Входной сигнал задается функцией Установившаяся ошибка Построим график ошибки в программном пакете Matlab/simulink (рисунок 43). Для построения используем модель, отображенную на рисунке 43. Как видно из рисунка 44, установившаяся ошибка стремится к расчетной.
Рисунок 43 – Модель для построения графика ошибки при обработке линейно нарастающего сигнала
Рисунок 44 – График ошибки Для определения интервала времени, на котором практически устанавливается вынужденный режим, увеличим участок графика (рисунок 45). При определении примем Как видно из рисунка 45, вынужденный режим устанавливается за
Рисунок 45 – Участок графика ошибки для определения интервала времени, на котором устанавливается вынужденный режим
Гармонический сигнал В программном пакете Matlab/simulink построим график реакции системы по выходу ДОС при подаче на вход системы гармонического сигнала заданного в ТЗ (рисунок 47). Частота
Рисунок 46 – Модель для построения графика реакции на входное гармоническое воздействие по выходу ДОС
Рисунок 47 – Реакция системы по выходу ДОС на входное гармоническое воздействие
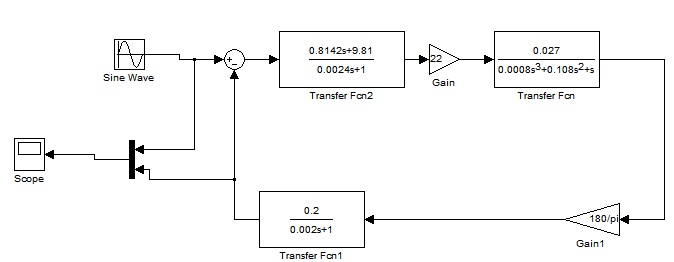
Определим амплитудно-фазовые искажения отработки входного сигнала. Построим графики входного и выходного сигнала в одной плоскости с помощью программного пакета Matlab в среде Simulink (рисунок 49). Используем модель, приведенную на рисунке 48.
Рисунок 48 – Модель для построения графиков выхода и входа
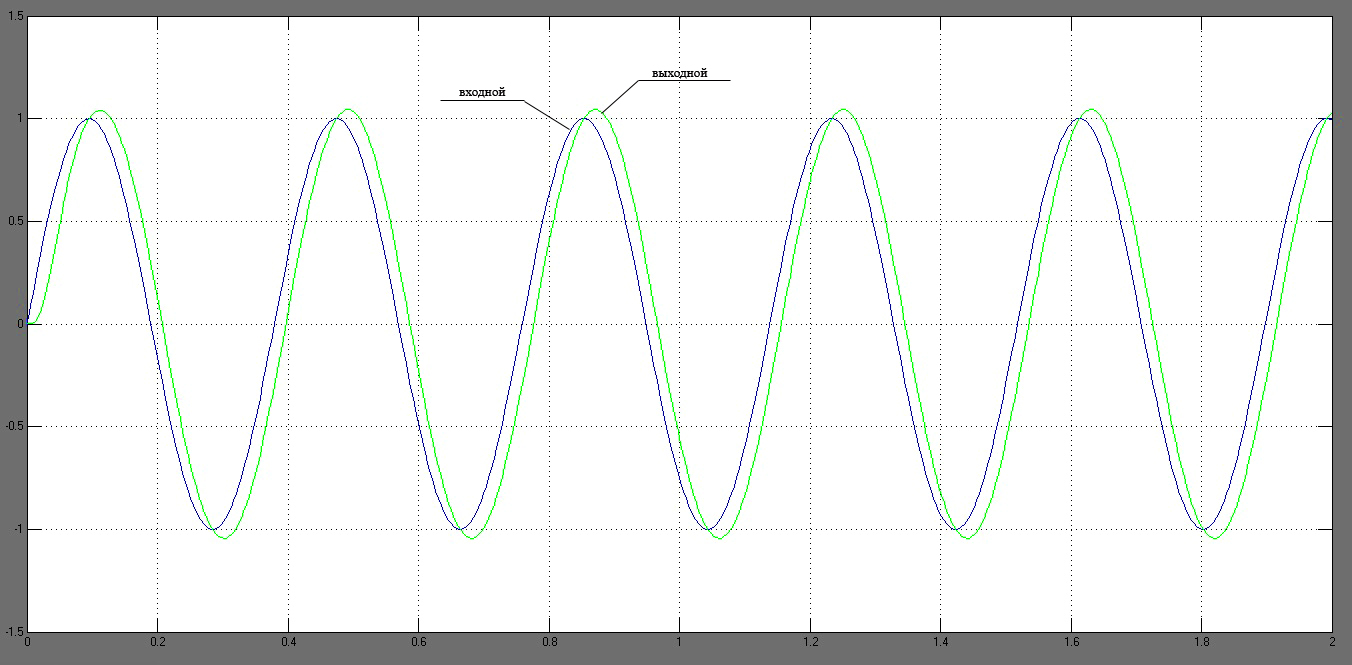
Рисунок 49 – Графики входного и выходного сигналов
Для определения искажений по амплитуде увеличим участок графика (рисунок 50). Амплитудные искажения
Рисунок 50 – Увеличенный участок графика для определения амплитудных искажений
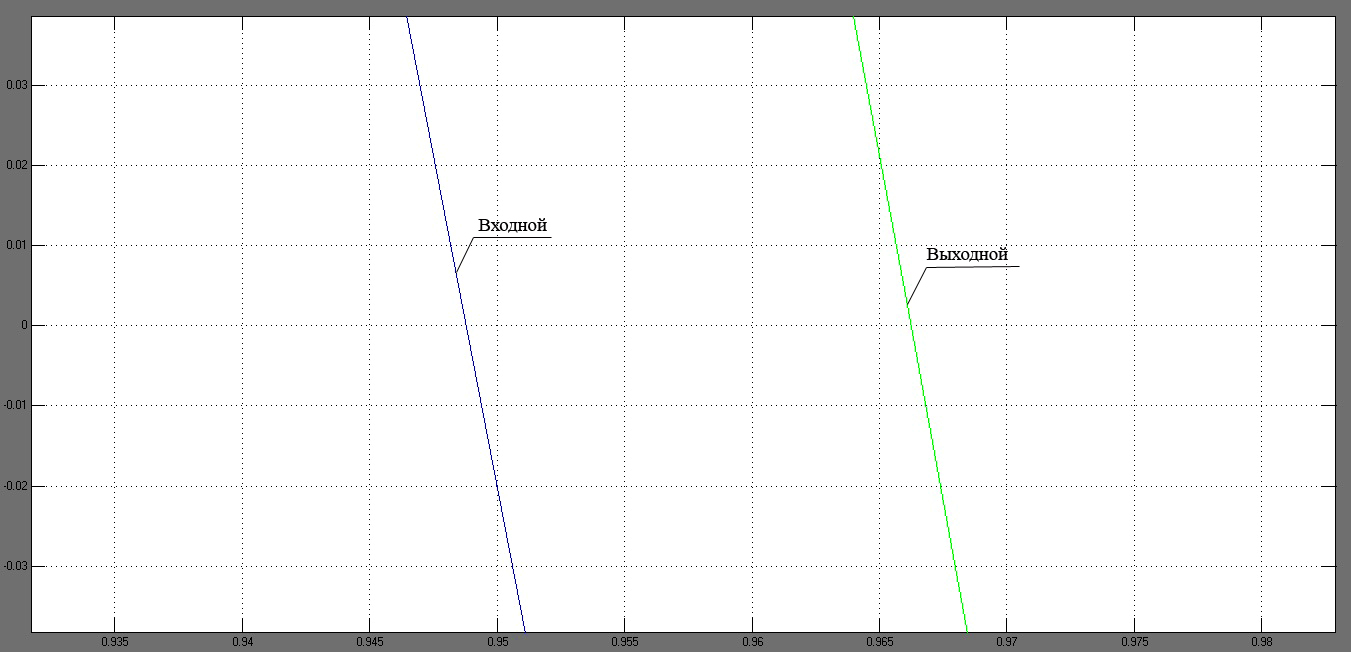
Рисунок 51 – Увеличенный участок для нахождения фазовых искажений По рисунку 51 видно, что Тогда фазовые искажения Найдем амплитудно-фазовые искажения по частотным характеристикам. По модели системы изображенной на рисунке 46 построим ЛАЧХ и ЛФЧХ замкнутой системы в программном пакете Matlab/simulink (рисунок 52).
Рисунок 52 – Нахождение АФИ по ЛЧХ Амплитудные искажения – Фазовые искажения – Из расчетов приведенных выше видно, что искажения, найденные по ЛЧХ, и искажения, найденные при отработке системой гармонического сигнала, незначительно отличаются, что связано с погрешностями.
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1841; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.238.81 (0.01 с.) |

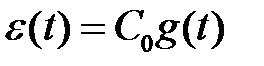 , где
, где  .
.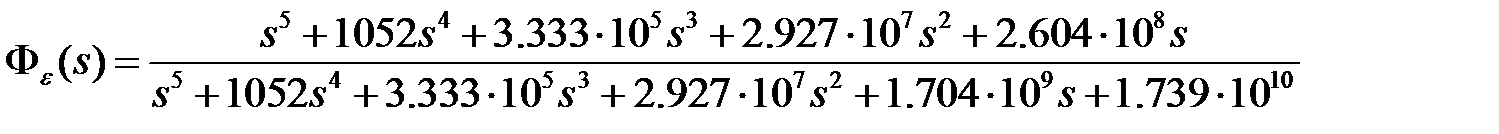
 .
.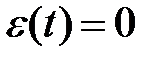 , что объясняется наличием в прямой цепи интегратора.
, что объясняется наличием в прямой цепи интегратора. , определим частоту
, определим частоту 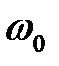 . Определим передаточную функцию системы по выходу усилителя мощности.
. Определим передаточную функцию системы по выходу усилителя мощности. ;
;
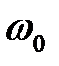 по АЧХ
по АЧХ рад/с.
рад/с. . Найти ошибку, значит определить
. Найти ошибку, значит определить 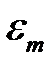 и
и  .
. ;
;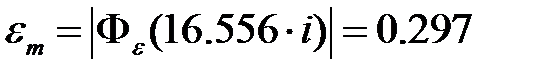 ;
;
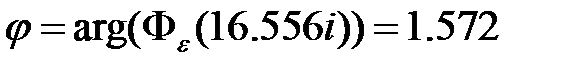 рад.
рад.

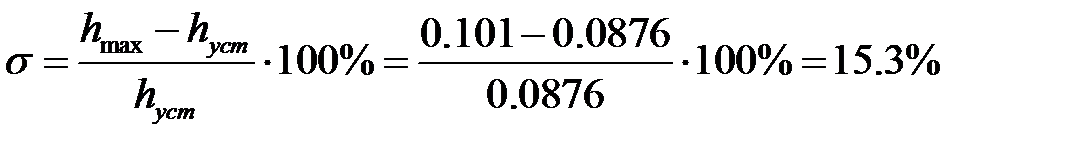 ;
; с.
с. ,
,  с.
с.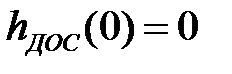 ;
; 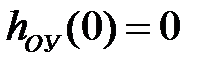 ;
; 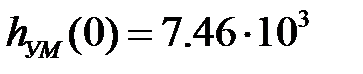 – начальные значения.
– начальные значения.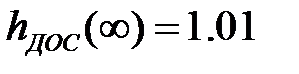 ;
;  ;
; 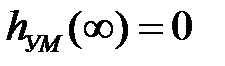 – установившиеся значения
– установившиеся значения , при котором система работает в зоне линейности усилителя мощности.
, при котором система работает в зоне линейности усилителя мощности.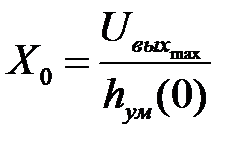 ;
;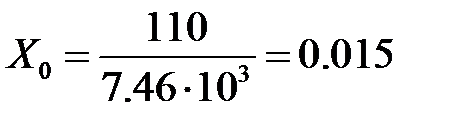 ;
;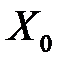 выходам ОУ, ДОС и УМ. Для этого реакции системы отобразим на графиках (рисунки 39, 40,41).
выходам ОУ, ДОС и УМ. Для этого реакции системы отобразим на графиках (рисунки 39, 40,41).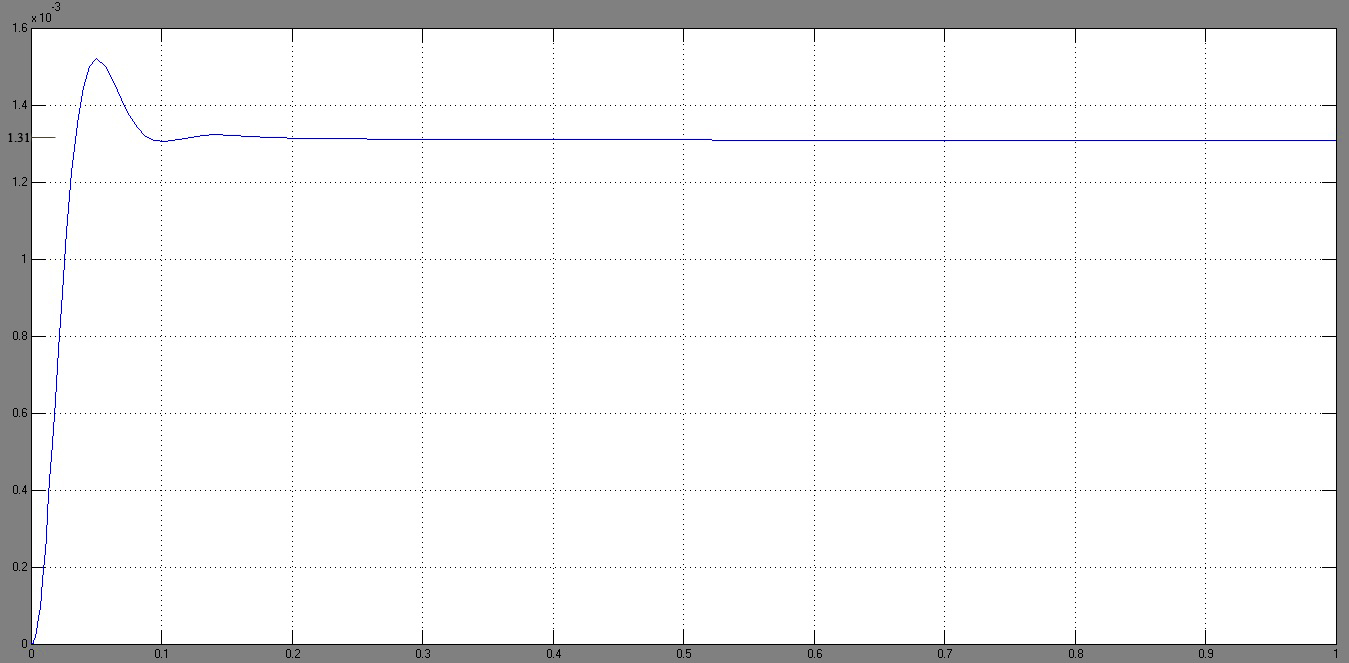
 по выходу ОУ
по выходу ОУ

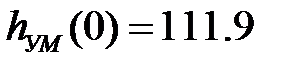 – начальные значения.
– начальные значения.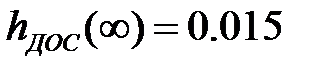 ;
;  ;
;  ;
; − коэффициенты ошибок.
− коэффициенты ошибок.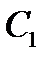 найдем с помощью программного пакета MathCAD 15 (рисунок 42).
найдем с помощью программного пакета MathCAD 15 (рисунок 42).
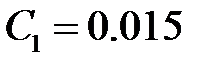 .
.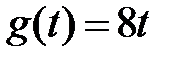 , тогда
, тогда 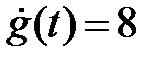 .
. .
.
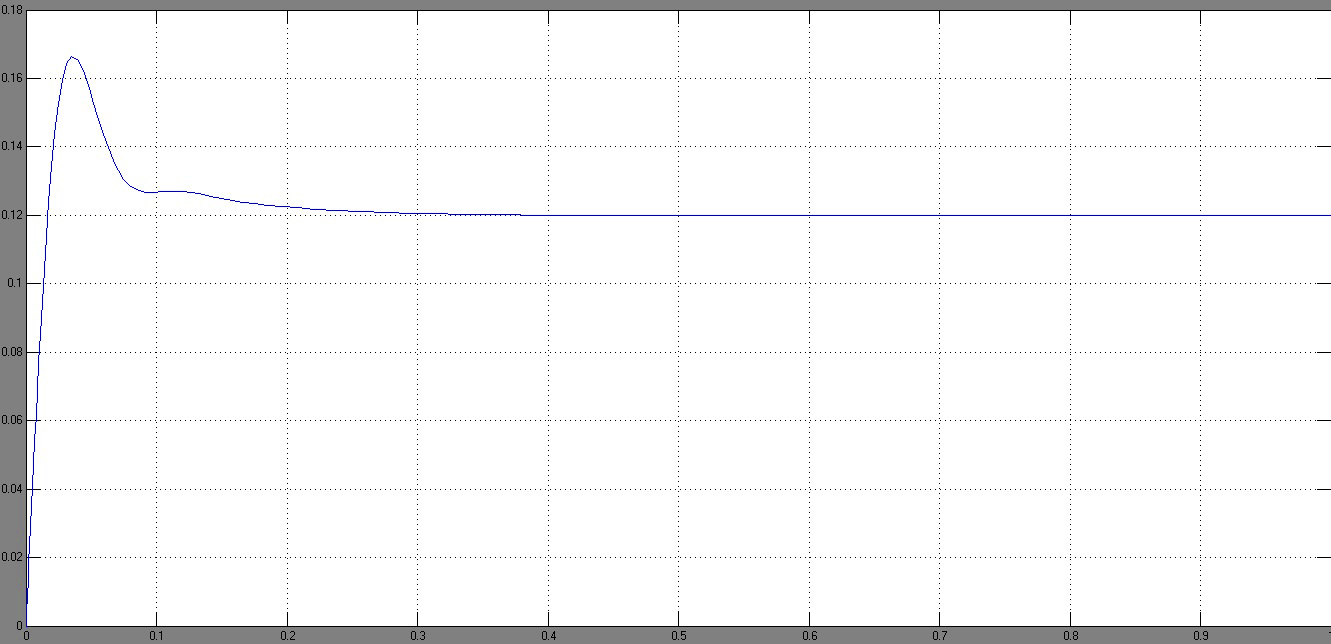
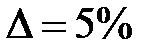 .
. с., что примерно в 2 раза больше чем время регулирования
с., что примерно в 2 раза больше чем время регулирования 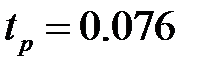 с.
с.
 этого сигнала определена ранее в пункте 2.5.4. Для построения графика используем модель, отображенную на рисунке 46.
этого сигнала определена ранее в пункте 2.5.4. Для построения графика используем модель, отображенную на рисунке 46.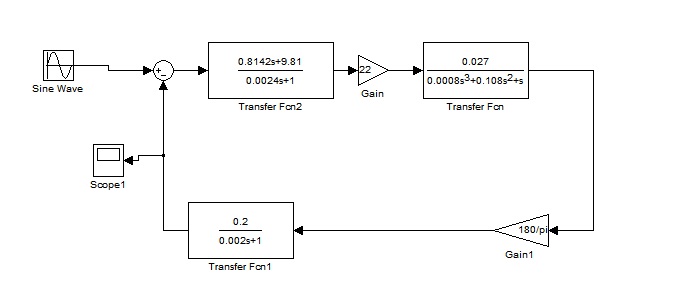

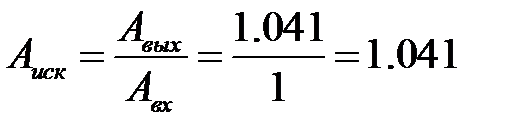 . Для определения фазовых искажений увеличим график в окрестности пересечения функциями оси t (рисунок 51).
. Для определения фазовых искажений увеличим график в окрестности пересечения функциями оси t (рисунок 51).
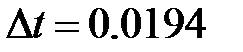 с.
с. град.
град.
 .
.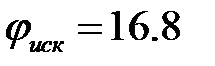 град.
град.


