
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функциональная схема замкнутой системыСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Введение В данной работе проводится динамический синтез системы автоматического управления углом поворота. Такие системы очень распространены в наше время, т.к. имеют широкую область применения, в том числе в системах управления летательными аппаратами. Цели работы – получение навыков по корректировке систем управления, синтезу регуляторов, а также закрепление знаний по анализу нелинейных СУ.
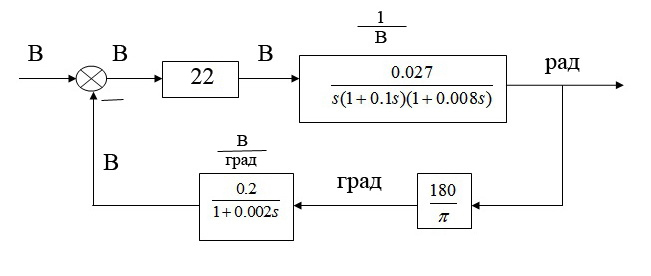
Анализ исходной системы Функциональная схема замкнутой системы Функциональная схема заданной системы приведена на рисунке 1.
Рисунок 1 – Функциональная схема системы В данной схеме: ЭС – элемент сравнения, УМ – усилитель мощности, ОУ – объект управления, ДОС – датчик обратной связи, КС – кинематическая связь. Математическое описание УМ и КС см. приложение Г. Передаточные функции ОУ и ДОС:
Структурная схема исходной системы Подставив известные передаточные функции блоков, проведя линеаризацию и определив размерности сигналов и блоков, получим структурную схему системы (рисунок 2). При линеаризации воздействия нелинейных блоков не учтены, а действие УМ учитывается на линейном участке.
Рисунок 2 – Структурная схема исходной системы
Управляемая величина измеряется в радианах. Анализ устойчивости исходной линеаризованной системы по алгебраическому критерию Для того чтобы проанализировать систему по алгебраическому критерию запишем передаточную функцию системы:
Исходная система имеет 4 порядок. Запишем характеристическое уравнение:
Т.к. все Для проверки достаточного условия запишем определитель Гурвица:
Т.к. 1.4 Анализ соответствия исходной системы требованиям ТЗ Основные требования к системе по ТЗ: 1) Амплитудно-фазовые искажения при воспроизведении гармонического сигнала в полосе 0..0.15 Гц ≤ 0.2 дБ и 1 градус, 0.15..0.5 Гц ≤ 0.6 дБ и 4 градуса, 0.5..1.7 Гц ≤ 3 дБ и 12 градусов. 2) Время регулирования – не более 0.25 с. 3) Перерегулирование – не более 35 % Заданные показатели качества системы определяются по выходу датчика обратной связи.
Рисунок 3 – Модель системы в среде simulink
Рисунок 3a – Переходная характеристика системы по выходу ДОС
Рисунок 4 – ЛАЧХ и ЛФЧХ системы (по выходу ДОС) Перерегулирование в системе Время регулирования – 0.64 с. Амплитудно-фазовые искажения при воспроизведении гармонического сигнала в полосах: 0..0.15 Гц – 0.045 дБ и 8.45 град. (рисунок 5) 0.15..0.5 Гц – 0.383 дБ и 28.7 град. (рисунок 6) 0.5..1.7 Гц – 3.31 дБ и 114 град (рисунок 7)
Рисунок 5 – 1 участок ЛЧХ
Рисунок 6 – 2 участок ЛЧХ
Рисунок 7 – 3 участок ЛЧХ
Исходная система не удовлетворяет требованиям ТЗ, т.к. гармонический сигнал воспроизводится с большими искажениями, а время регулирования превышает требуемое по ТЗ. Синтез регулятора Построение асимптотической ЛАЧХ нескорректированной системы Для построения ЛАЧХ нескорректированной системы вычислим частоты сопряжения и определим точку пересечения характеристикой оси L:
Построенная асимптотическая ЛАЧХ отображена в приложении А. Построение запретной области и низкочастотного участка желаемой ЛАЧХ Т.к. наложены ограничения на величину АФИ, то для построения низкочастотного участка желаемой ЛАЧХ и запретной области заполним таблицу:
Для построения запретной области вычислим координаты точек «излома» области:
Построенная запретная область приведена в приложении А. Минимальный коэффициент усиления выбираем из условия
Тогда желаемая ЛАЧХ должна пересечь ось L в точке:
Т.к. низкочастотная асимптота проводится с наклоном -20 дБ/дек, то при данном коэффициенте усиления асимптота попадет в запретную область. Для предотвращения попадания асимптоты в запретную область увеличим коэффициент усиления до Тогда желаемая ЛАЧХ пересечет ось L в точке:
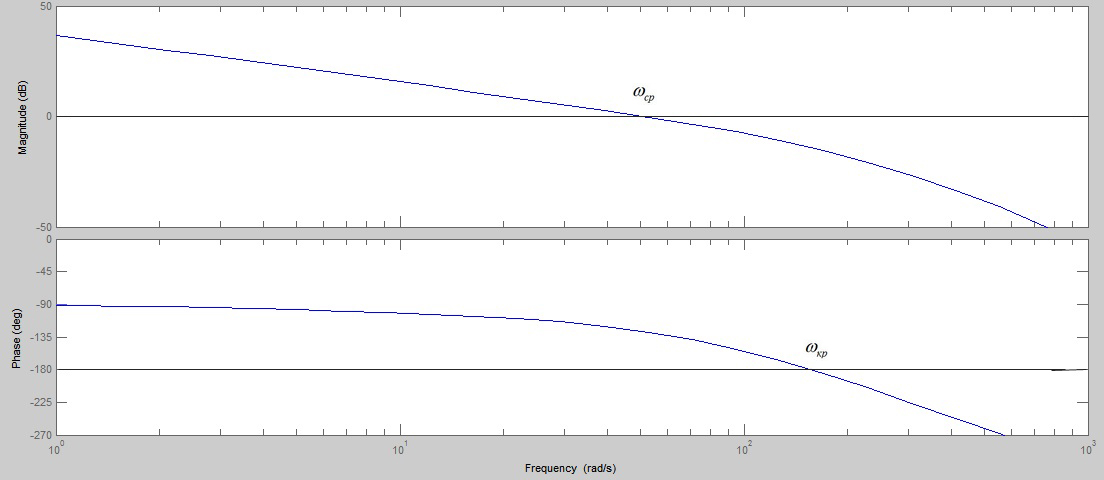
Проведем низкочастотную асимптоту с наклоном -20 дБ/дек до частоты Анализ скорректированной системы в частотной области Анализ устойчивости системы Для проведения анализа устойчивости системы воспользуемся критериями Найквиста на плоскостях ЛЧХ и АФЧХ и критерием Михайлова. В программном пакете Matlab построим логарифмические частотные характеристики разомкнутой системы (рисунок 16).
Рисунок 16 – Модель разомкнутой системы в Matlab
Рисунок 17 – Критерий Найквиста на плоскости ЛЧХ Согласно критерию Найквиста на плоскости ЛЧХ разомкнутой системы, для устойчивости системы необходимо и достаточно чтобы частота среза была меньше критической частоты. Из рисунка 16 видно, что для скорректированной системы это условие выполняется, значит, система устойчива. Для применения критерия Найквиста на плоскости АФЧХ запишем передаточную функцию разомкнутой системы и перейдем от нее к частотной передаточной функции.
Найдем корни характеристического уравнения.
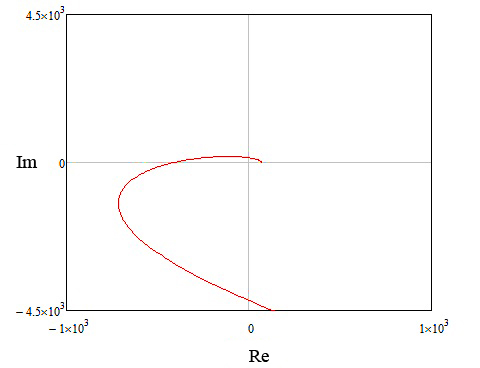
Т.к. С помощью программного пакета MathCAD построим АФЧХ системы (рисунки 18,19).
Рисунок 18 – Параметры заданные в MathCAD для построения АФЧХ
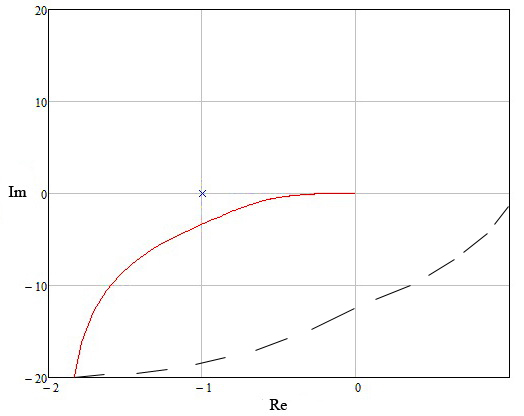
Рисунок 19 – АФЧХ системы Если разомкнутая система на границе устойчивости, то для устойчивости замкнутой системы необходимо чтобы годограф Найквиста (АФЧХ), дополненный на участке разрыва дугой бесконечно большого радиуса, не охватывал особую точку (-1;0). Как видно из рисунка 19, годограф Найквиста не охватывает особую точку, а значит, замкнутая система устойчива. Для того чтобы воспользоваться критерием Михайлова сформируем функцию Михайлова. Для этого передаточную функцию замкнутой системы.
Выпишем характеристическое уравнение замкнутой системы, подставив
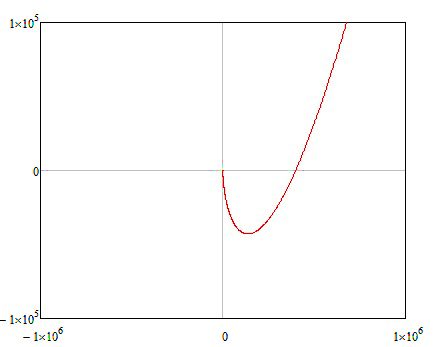
В программном пакете MathCAD построим годограф Михайлова, выделив действительную и мнимую часть функции.
Рисунок 20 – Годограф Михайлова при прохождении первых четырех квадрантов
Рисунок 21 – Годограф Михайлова при прохождении пятого квадранта Для устойчивости замкнутой системы необходимо и достаточно чтобы годограф Михайлова начинался на вещественной положительной полуоси и при увеличении частоты от 0 до Т.к. система 5-ого порядка, годограф Михайлова должен последовательно пройти пять квадрантов, что и отображено на рисунках 20 и 21. Условия критерия Михайлова выполняются, значит, система устойчива. 2.5.2 Анализ системы на соответствие ее требованиям ТЗ Основные требования к системе по ТЗ: 1) Амплитудно-фазовые искажения при воспроизведении гармонического сигнала в полосе 0..0.15 Гц ≤ 0.2 дБ и 1 градус, 0.15..0.5 Гц ≤ 0.6 дБ и 4 градуса, 0.5..1.7 Гц ≤ 3 дБ и 12 градусов. 2) Время регулирования – не более 0.25 с. 3) Перерегулирование – не более 35 % Заданные показатели качества системы определяются по выходу датчика обратной связи.
Для определения амплитудно-фазовых искажений при отработке системой гармонического сигнала, в программном пакете Matlab построим ЛАЧХ и ЛФЧХ системы по выходу ДОС. На рисунках 23, 24,25 отобразим полосы частот, в которых нужно проверить АФИ. Модель замкнутой системы, с помощью которой построены характеристики, приведена на рисунке 22.
Рисунок 22 – Модель замкнутой системы в среде Simulink (Matlab)
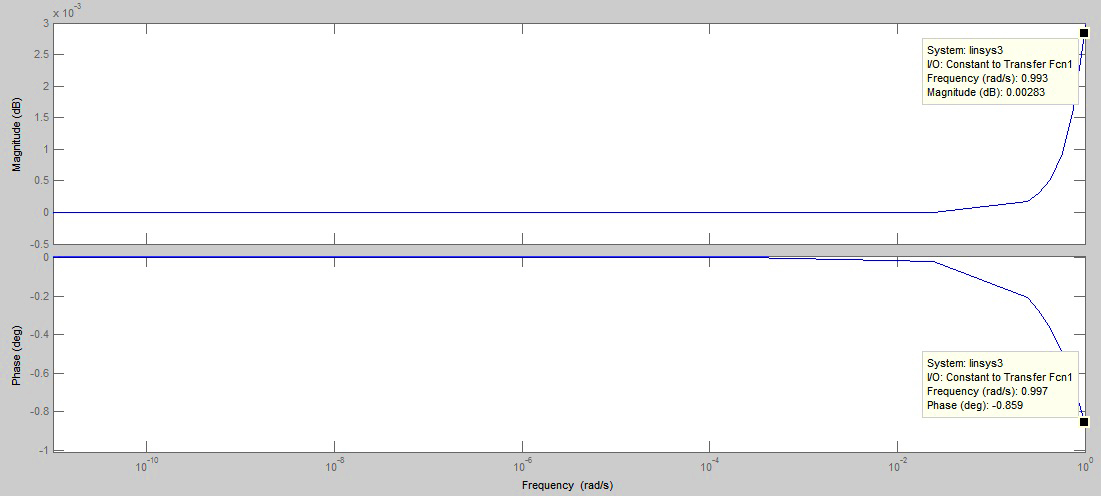
Рисунок 23 – 1 полоса частот
Рисунок 24 – 2 полоса частот
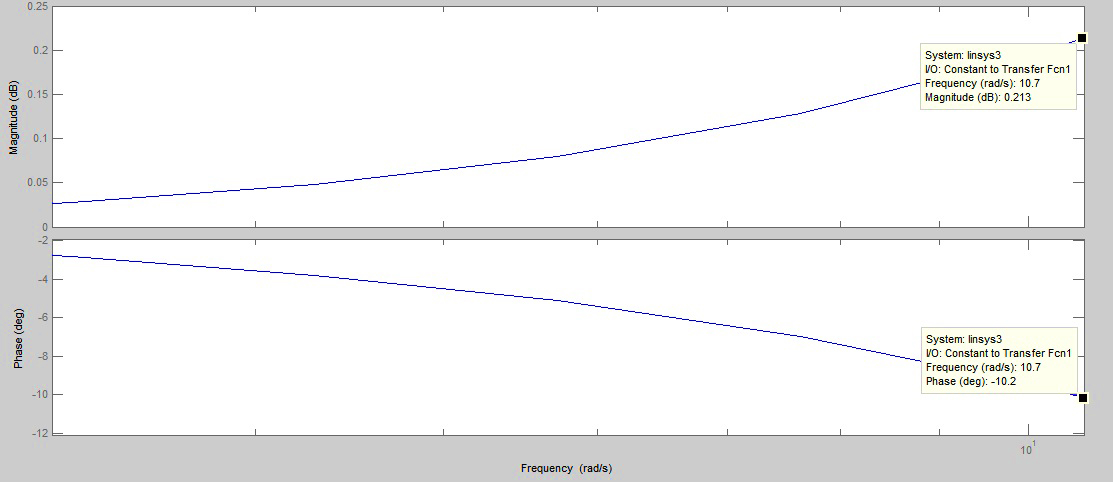
Рисунок 25 – 3 полоса частот Как видно из рисунков 22,23,24 АФИ скорректированной системы удовлетворяют требованиям ТЗ. Для того чтобы определить перерегулирование и время переходного процесса построим переходную характеристику h(t) по выходу ДОС (рисунок 26). На рисунке 26 видно, что Для оценки времени переходного процесса примем
Рисунок 26 – Переходная характеристика системы по выходу ДОС Приведенный выше анализ показывает, что все показатели качества скорректированной системы удовлетворяют требованиям ТЗ. Гармонический сигнал В программном пакете Matlab/simulink построим график реакции системы по выходу ДОС при подаче на вход системы гармонического сигнала заданного в ТЗ (рисунок 47). Частота
Рисунок 46 – Модель для построения графика реакции на входное гармоническое воздействие по выходу ДОС
Рисунок 47 – Реакция системы по выходу ДОС на входное гармоническое воздействие
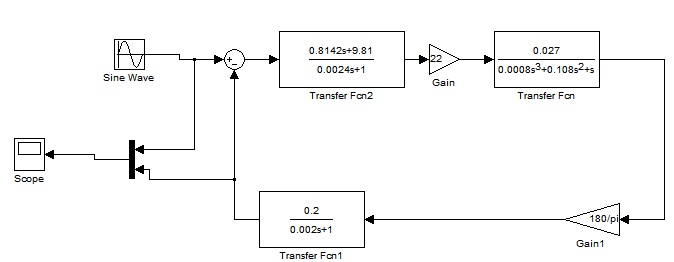
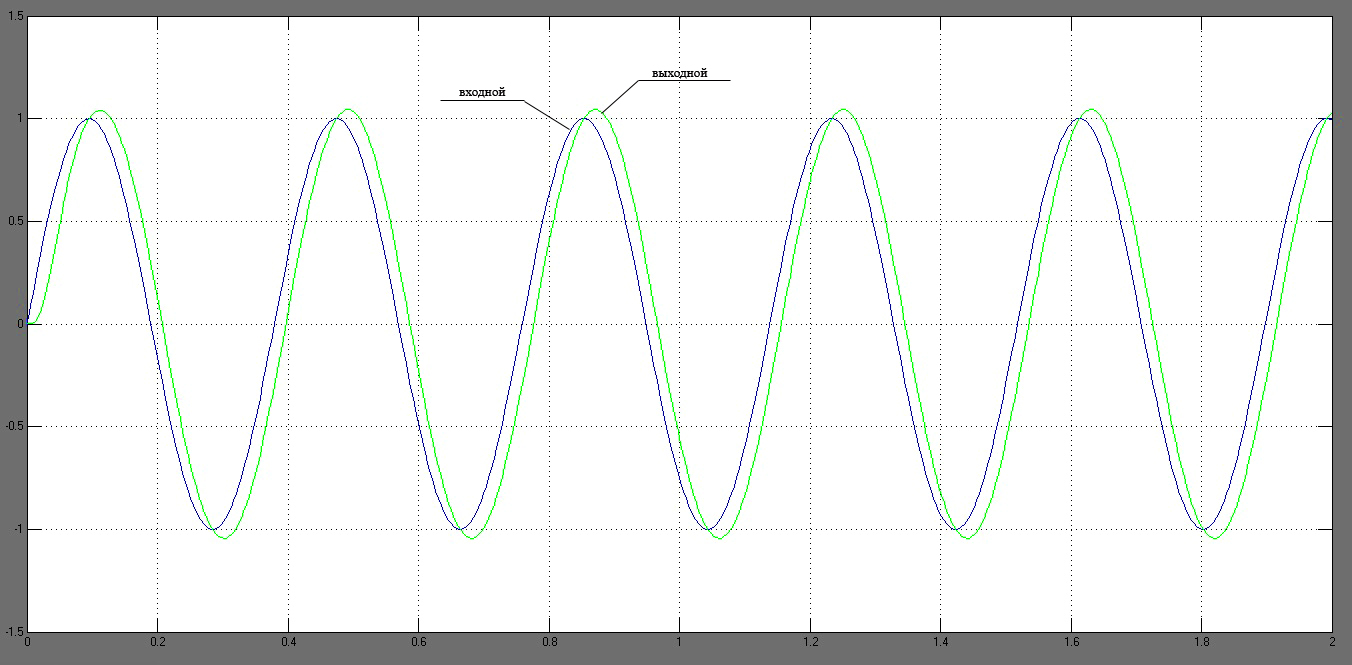
Определим амплитудно-фазовые искажения отработки входного сигнала. Построим графики входного и выходного сигнала в одной плоскости с помощью программного пакета Matlab в среде Simulink (рисунок 49). Используем модель, приведенную на рисунке 48.
Рисунок 48 – Модель для построения графиков выхода и входа
Рисунок 49 – Графики входного и выходного сигналов
Для определения искажений по амплитуде увеличим участок графика (рисунок 50). Амплитудные искажения
Рисунок 50 – Увеличенный участок графика для определения амплитудных искажений
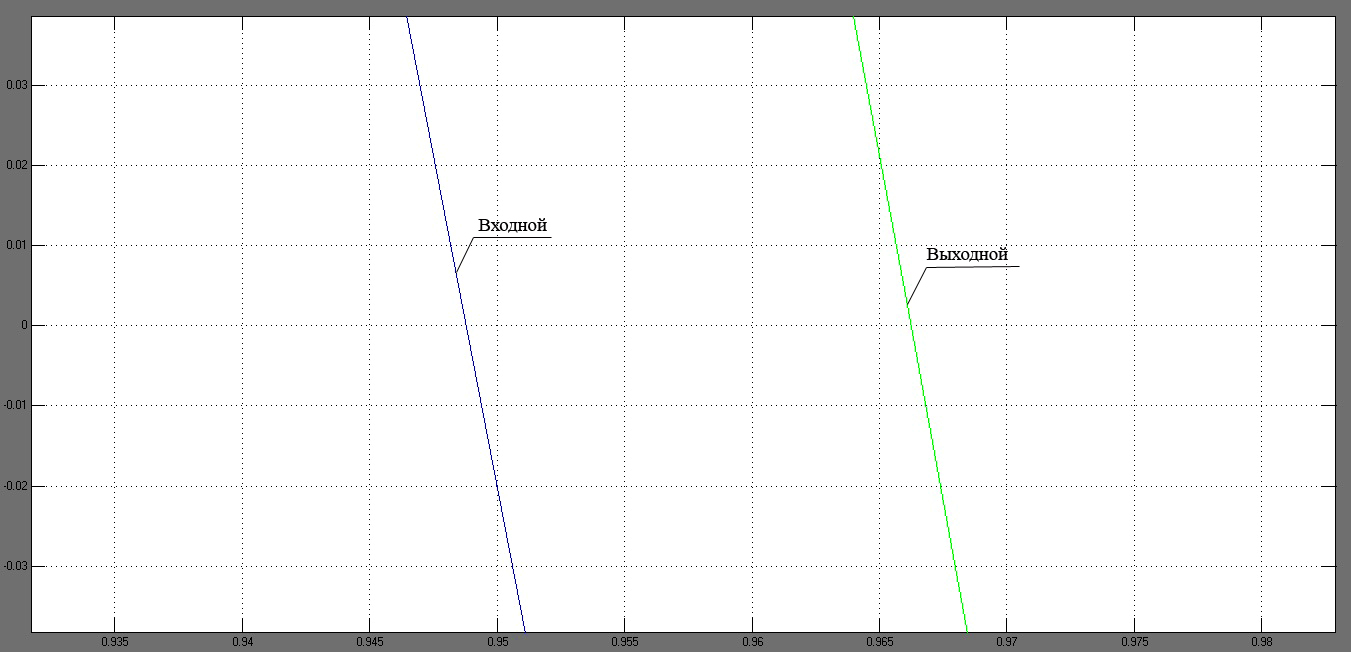
Рисунок 51 – Увеличенный участок для нахождения фазовых искажений По рисунку 51 видно, что Тогда фазовые искажения Найдем амплитудно-фазовые искажения по частотным характеристикам. По модели системы изображенной на рисунке 46 построим ЛАЧХ и ЛФЧХ замкнутой системы в программном пакете Matlab/simulink (рисунок 52).
Рисунок 52 – Нахождение АФИ по ЛЧХ Амплитудные искажения – Фазовые искажения – Из расчетов приведенных выше видно, что искажения, найденные по ЛЧХ, и искажения, найденные при отработке системой гармонического сигнала, незначительно отличаются, что связано с погрешностями. Заключение В ходе выполнения курсовой работы было установлено, что исходная система не удовлетворяет требованиям технического задания. Для корректировки системы был проведен синтез регулятора, после чего характеристики системы значительно улучшились и стали соответствовать ТЗ. Затем был проведен расширенный анализ полученной СУ, который показал, что система устойчива (по критериям Найквиста и Михайлова). Были определены запасы устойчивости, а также характеристики системы в переходном и установившемся режиме. Также была исследована точность системы, рассчитаны и построены графики ошибок при отработке системой линейного и гармонического сигналов. Также был проведен анализ системы с учетом нелинейности усилителя мощности и люфта в кинематической передаче.
Библиографический список 1. Бесекерский, В.А.Теория систем автоматического регулирования / В.А. Бесекерский, Е.П. Попов. – 3-е изд. – Москва: Наука, 1975. – 767с. 2. Макаров, И.М. Линейные автоматические системы / И.М. Макаров, Б.М. Менский. – 2-е изд. – Москва: Машиностроение, 1982. – 504 с. 3. Павловская, О.О. Теория автоматического управления: учебное пособие к лабораторным и курсовым работам / О.О. Павловская, И.В. Чернецкая. – Челябинск: Издательский центр ЮУрГУ, 2010. – 93 с. 4. Долбенков, В.И. Simulink в задачах систем автоматического управления: учебное пособие / В.И. Долбенков. – Челябинск: Изд-во ЮУрГУ, 2005. – 101 с. Приложение А. Исходная и желаемая ЛАЧХ
Приложение Б. Увеличенные графики реакций системы по выходу ДОС для пункта 5.1
Рисунок 76 – Увеличенный график реакции на
Рисунок 77 – Увеличенный график реакции на
Рисунок 78 – Увеличенный график реакции на
Рисунок 79 – Увеличенный график реакции на
Рисунок 80 – Увеличенный график реакции на
Рисунок 81 – Увеличенный график реакции на единичный сигнал для определения времени переходного процесса
Приложение В. Построение годографов в пункте 5.3 с помощью MathCAD
Рисунок 82 – МаthCAD-выкладки для построения годографов
Приложение Г. Математическое описание УМ и КС
Рисунок 83 – Зона насыщения усилителя мощности Математически усилитель мощности можно описать функцией:
В кинематической связи нашей системы проявляется люфт, который можно описать графически:
Рисунок 84 – Люфт
Введение В данной работе проводится динамический синтез системы автоматического управления углом поворота. Такие системы очень распространены в наше время, т.к. имеют широкую область применения, в том числе в системах управления летательными аппаратами. Цели работы – получение навыков по корректировке систем управления, синтезу регуляторов, а также закрепление знаний по анализу нелинейных СУ.
Анализ исходной системы Функциональная схема замкнутой системы Функциональная схема заданной системы приведена на рисунке 1.
Рисунок 1 – Функциональная схема системы В данной схеме: ЭС – элемент сравнения, УМ – усилитель мощности, ОУ – объект управления, ДОС – датчик обратной связи, КС – кинематическая связь. Математическое описание УМ и КС см. приложение Г. Передаточные функции ОУ и ДОС:
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 759; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.214.28 (0.011 с.) |



 .
.
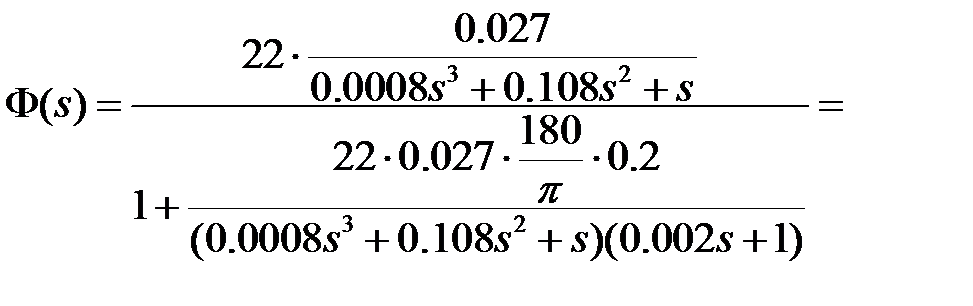
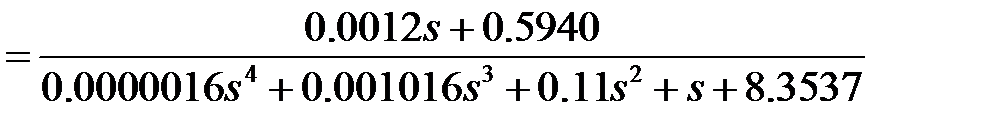

 одного знака, то необходимое условие устойчивости по алгебраическому критерию выполняется.
одного знака, то необходимое условие устойчивости по алгебраическому критерию выполняется.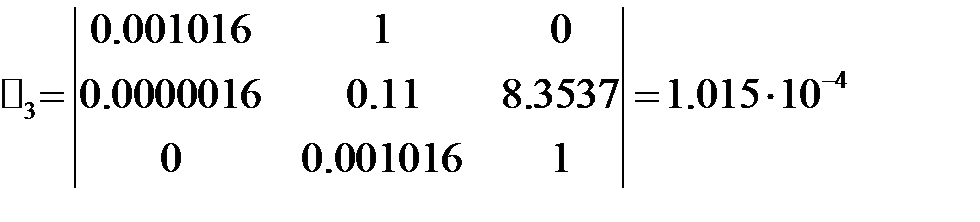 ;
; , то достаточное условие устойчивости по алгебраическому критерию выполняется – значит, система устойчива.
, то достаточное условие устойчивости по алгебраическому критерию выполняется – значит, система устойчива.


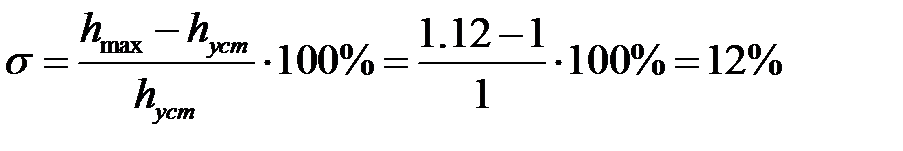



 рад;
рад; 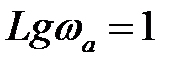 дек
дек рад;
рад;  дек
дек рад;
рад;  дек
дек ;
;  дБ
дБ , рад/с
, рад/с
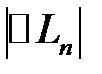 , дБ
, дБ

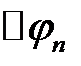 , град
, град


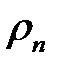

 дек;
дек;  дБ;
дБ; дек;
дек;  дБ;
дБ; дек;
дек;  дБ.
дБ.
 ;
; дБ
дБ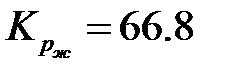 .
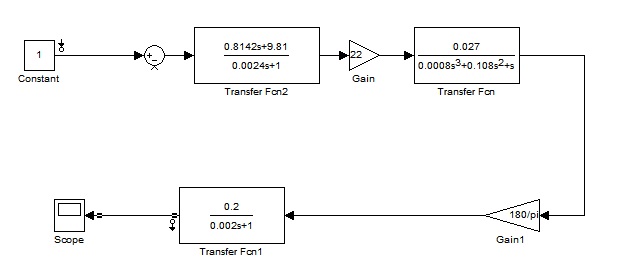
. дБ
дБ .
.
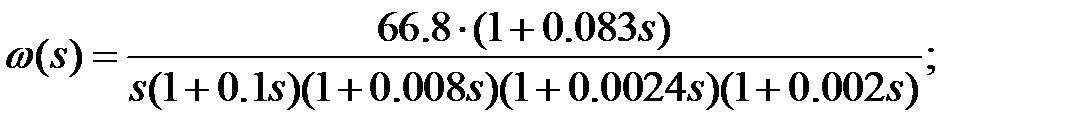
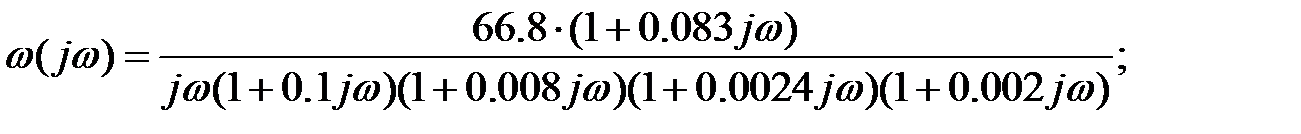
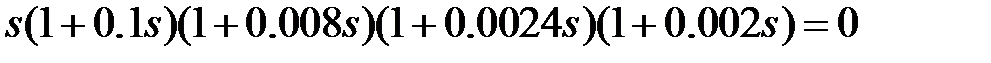 ;
;
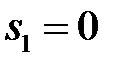 , то разомкнутая система на границе устойчивости.
, то разомкнутая система на границе устойчивости.
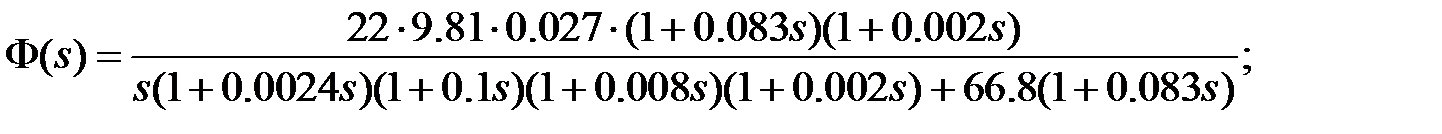
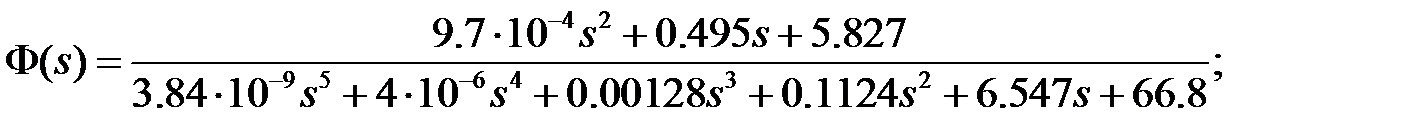
 вместо s. Это и будет функция Михайлова.
вместо s. Это и будет функция Михайлова.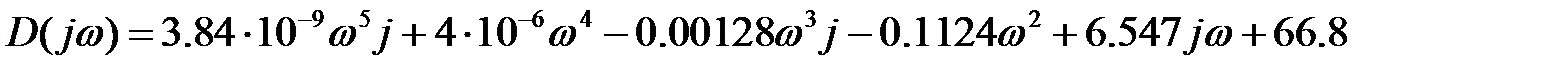 ;
;
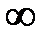 проходил в положительном направлении (против часовой стрелки) столько квадрантов, каков порядок системы, при чем прохождение последовательное, не попадая в начало координат.
проходил в положительном направлении (против часовой стрелки) столько квадрантов, каков порядок системы, при чем прохождение последовательное, не попадая в начало координат.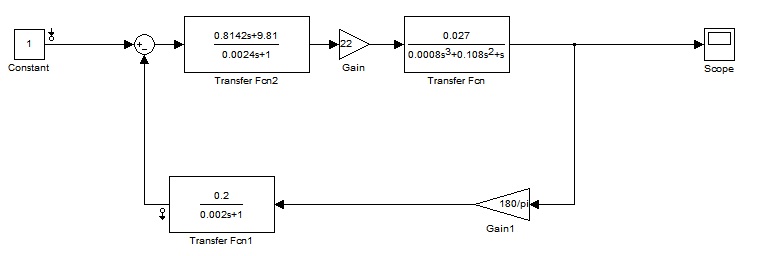

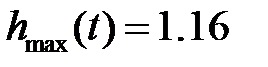 , а
, а 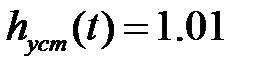 , тогда перерегулирование
, тогда перерегулирование 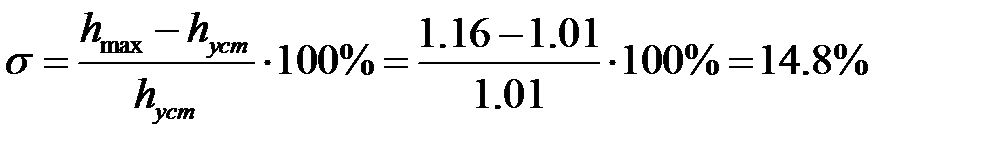 .
.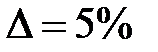 . Тогда
. Тогда 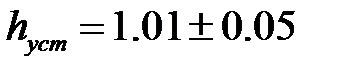 . По рисунку 26 видно, что время переходного процесса
. По рисунку 26 видно, что время переходного процесса 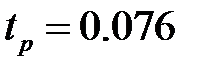 с.
с.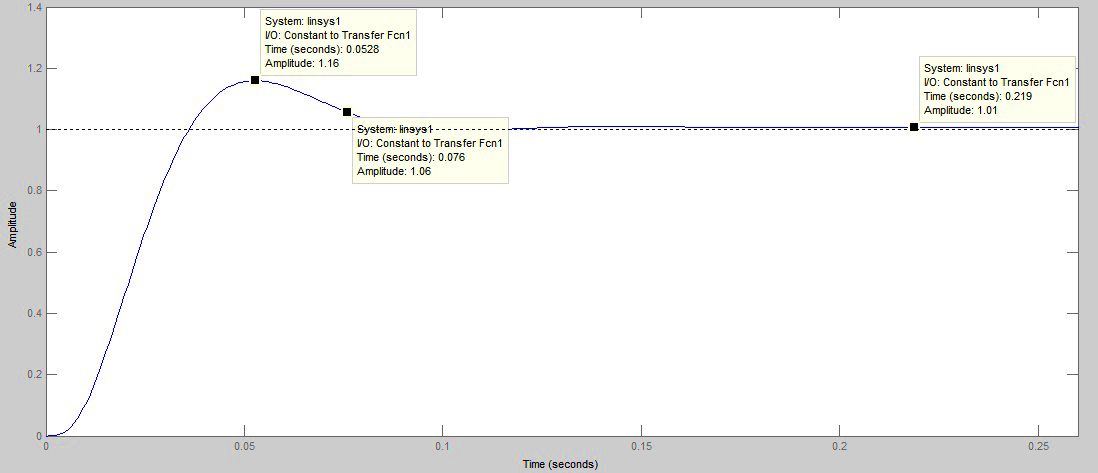
 этого сигнала определена ранее в пункте 2.5.4. Для построения графика используем модель, отображенную на рисунке 46.
этого сигнала определена ранее в пункте 2.5.4. Для построения графика используем модель, отображенную на рисунке 46.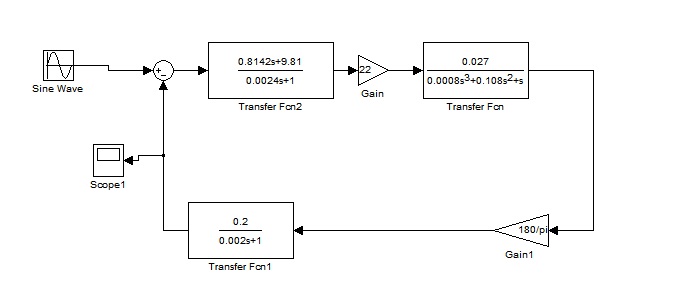

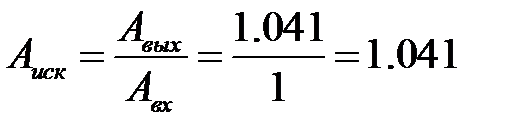 . Для определения фазовых искажений увеличим график в окрестности пересечения функциями оси t (рисунок 51).
. Для определения фазовых искажений увеличим график в окрестности пересечения функциями оси t (рисунок 51).
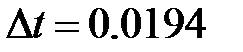 с.
с. град.
град.
 .
.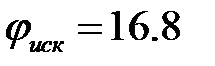 град.
град.
 для определения перерегулирования
для определения перерегулирования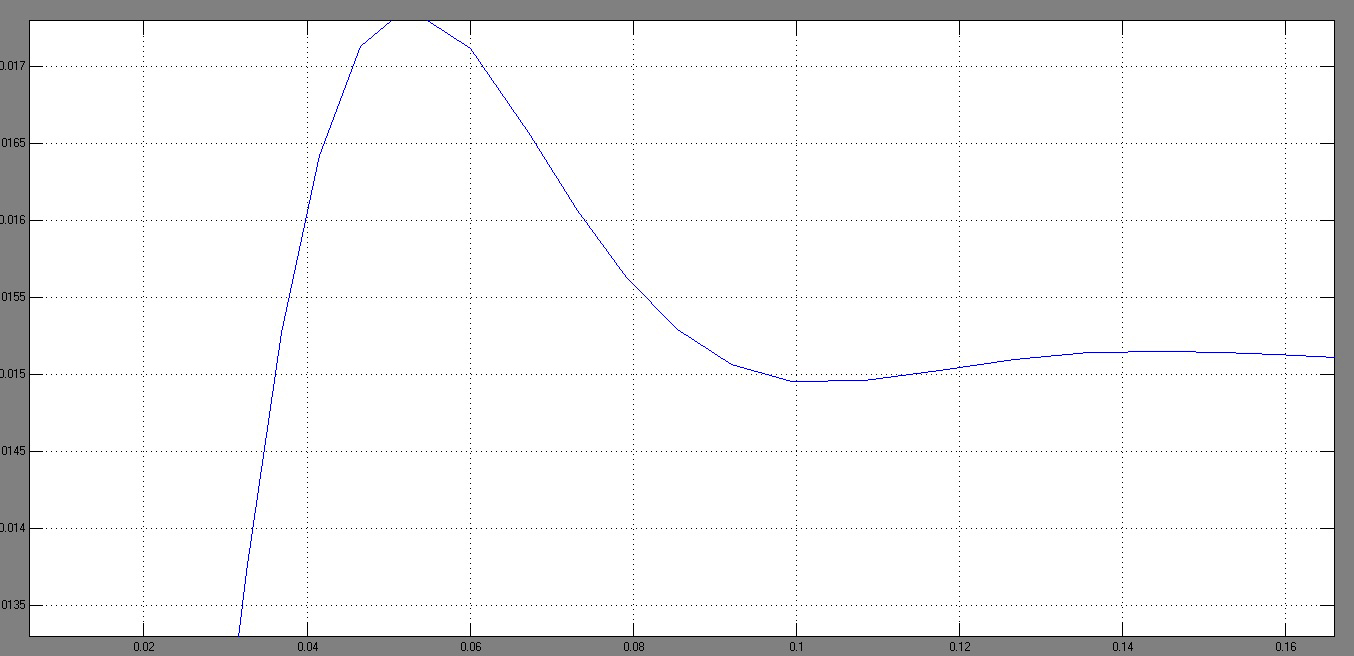

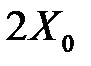 для определения перерегулирования
для определения перерегулирования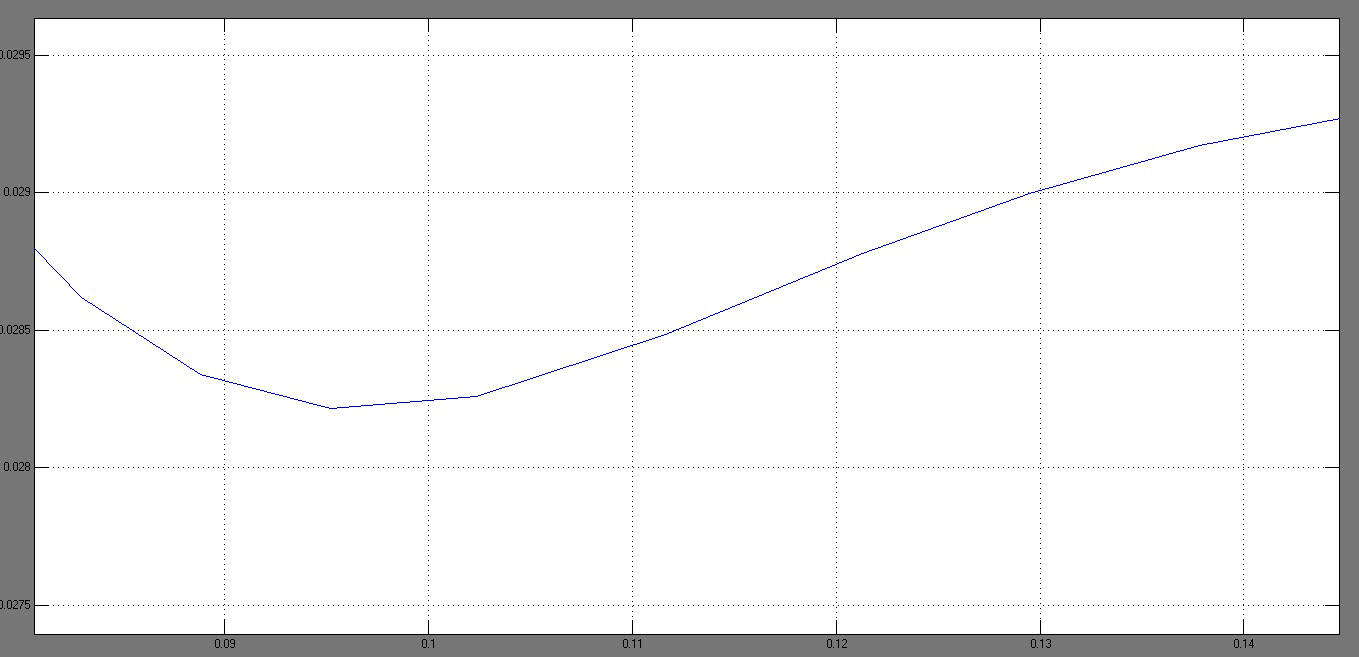
 для определения времени переходного процесса
для определения времени переходного процесса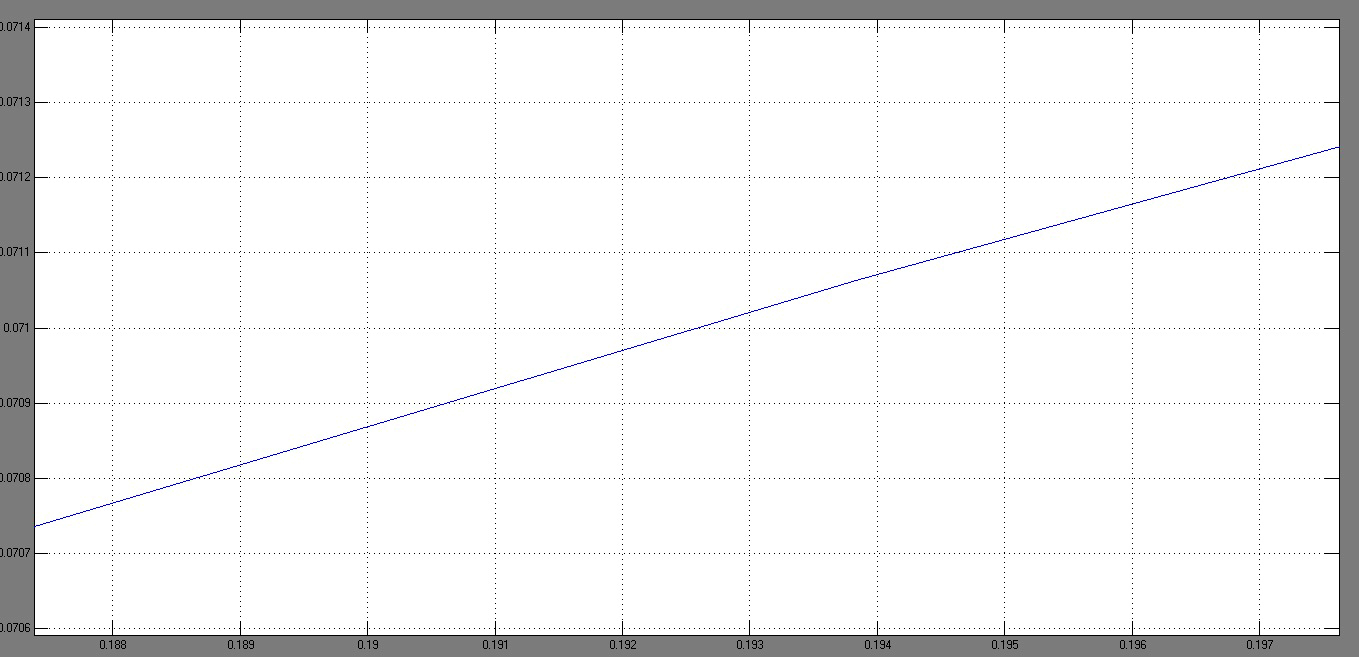
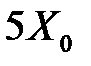 для определения времени переходного процесса
для определения времени переходного процесса







