Тема 3. Вынужденные колебания. Резонанс

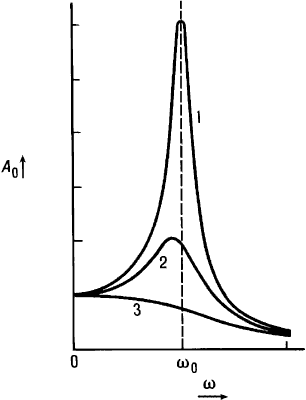
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:

Резонанс - (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле: ,

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках). Резонансные явления могут вызвать необратимые разрушения в различных механических системах. Резонансный контур лежит в основе принципа действия мобильного телефона, ноутбука с адаптером беспроводной сети, автомобильного радиоприемника.

 

График зависимости вынужденных колебаний от частоты.

 

 

Тема 4. Сложные колебания

Всякое сложное колебание состоит из ряда простых синусоидальных колебаний - основного и высших гармоник. Форма сложного колебания может быть самой различной, в зависимости от того, сколько гармоник входит в его состав, какие у них частоты, амплитуды и начальные фазы. Примером сложных колебаний служит электрокардиограмма и электроэнцефалограмма.

Электрокардиограмма в 12 стандартных отведениях у мужчины 26 лет, без патологии.

 

 

Раздел 2. УПРУГИЕ ВОЛНЫ.

Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью v. Процесс распространения колебаний в пространстве называется волной.

Механизм возникновения волн. На рисунке показано движение частиц при распространении в среде поперечной волны. Номерами 1, 2 и т.д. обозначены частицы, отстоящие друг от друга на расстоянии 1/4 T, т.е. расстояние, проходимое волной за четверть периода колебаний, совершаемых частицами. В момент времени, принятый за нулевой, волна, распространяясь вдоль оси слева направо, достигла частицы 1, вследствие чего частица начала смещаться из положения равновесия вверх, увлекая за собой следующие частицы. Спустя четверть периода частица 1 достигнет крайнего верхнего положения; одновременно начинает смещаться из положения равновесия частица 2. По прошествии еще четверти периода частица 1 будет проходить положение равновесия, двигаясь в направлении сверху вниз, вторая частица 2 достигнет крайнего верхнего положения, а частица 3 начнет смещаться вверх из положения равновесия. В момент времени, равный T, частица 1 закончит полный цикл колебания, и будет находиться в таком же состоянии движения, как и в начальный момент времени. Волна к моменту времени T достигнет частицы 5.

На рисунке показаны колебания частиц, положения, равновесия которых лежат на оси x. В действительности колеблются не только частицы, расположенные вдоль оси x, а совокупность частиц в некотором объёме. Распространяясь от источника колебаний, волновой процесс охватывает всё новые и новые части пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом).

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт каждый момент времени только один. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической.

 

Расстояние λ, на которое распространяется волна за время, равное периоду колебания частиц среды, называется длиной волны. Очевидно, что: λ= vT,

где v - скорость волны, T - период колебаний. Длину волны можно определить также как расстояние между ближайшими точками среды, колеблющихся с разностью фаз, равной 2π. Заменив T через 1/ν, где v - частота колебаний, получим связь между длиной волны, частотой колебаний и скоростью распространения волны: λν=v.

Продольная волна – это волна, в которой частицы среды колеблются вдоль направления распространения волны. Поперечная - это волна, в которой частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Когда две одинаковые волны с равными амплитудами и периодами распространяются навстречу друг другу, то при их наложении возникают стоячие волны. Стоячие волны могут быть получены при отражении от препятствий. Допустим, излучатель посылает волну к препятствию (падающая волна). Отраженная от него волна наложится на падающую волну.

 

Тема 1. Интерференция

Интерференция волн — взаимное усиление или ослабление амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве. Волны и возбуждающие их источники называются когерентными, если разность фаз волн (φ₂-φ₁)не зависит от времени.

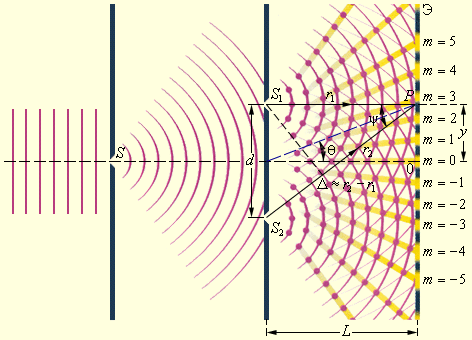
Волны при встрече могут усилить или ослабить друг друга.

Интерференция сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн. Интерферировать могут все волны, однако устойчивая интерференционная картина будет наблюдаться только в том случае, если волны имеют одинаковую частоту и колебания в них не ортогональны. Интерференция может быть стационарной и нестационарной. Стационарную интерференционную картину могут давать только полностью когерентные волны. Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников, при интерференции дадут результирующую волну, фронтом которой будет сфера.

Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S₁ и S₂ (рис. 1). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S₁ и S₂, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.

1)

 

Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S₁ и S₂, которые в соответствии с принципом Гюйгенса можно рассматривать как источники вторичных волн, освещались светом одного источника S. При симметричном расположении щелей вторичные волны, испускаемые источниками S₁ и S₂, находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r₁ и r₂. Следовательно, фазы колебаний, создаваемых волнами от источников S₁ и S₂ в точке P, вообще говоря, различны. Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами. Утверждение о том, что волны от источников S₁ и S₂ распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции.