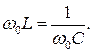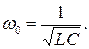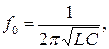Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные колебания в контуре без активного сопротивленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Электромагнитные колебания создаются с помощью электрических колебательных систем. Простейшей колебательной системой является колебательный контур. Колебательные контура широко используются в радиопередающих и радиоприёмных устройствах. С их помощью в радиопередатчиках создаются электромагнитные колебания с требуемой частотой, которые модулируются управляющими электрическими сигналами. В радиоприёмниках колебательные контуры осуществляют частотную избирательность, т. е. выделение ЭДС принимаемого сигнала из множества ЭДС, наводимых приемной антенной посторонними радио излучениями. Свободные или собственные колебания, возникают в контуре из-за некоторого первоначального запаса энергии, полученной от постороннего источника. Если к катушке индуктивности подключить предварительно заряженный конденсатор, то конденсатор начнет разряжаться через катушку.
По мере разряда конденсатора напряжение на конденсаторе уменьшается. В момент включения t0 ток через катушку равен 0, но с течением времени он возрастает, не смотря на то, что напряжение на конденсаторе уменьшается (т.е. еще быстрее уменьшается В тот момент, когда напряжение на конденсаторе уменьшиться до 0(t1) ток достигает своего максимума. Длительность времени до момента t1 зависит от емкости конденсатора и индуктивности катушки. По мере того, как возрастает ток через катушку, увеличивается и магнитное поле в катушке. В момент времени t1 энергия магнитного поля наибольшая ( С момента времени t1 ток не исчезает, а плавно уменьшается, существуя за счет энергии магнитного поля запасенной в катушке. Этот ток является зарядным для конденсатора. Если потери на активных сопротивлениях очень малы, то конденсатор перезарядится до такого же напряжения (U0), которое было на нем первоначально в момент времени t0. Причем полярность напряжения на конденсаторе изменится, так как направление тока при перезарядке такое же, как при разряде. Перезарядка длится до момента времени t2,пока вся энергия магнитного поля не перейдет в энергию электрического поля конденсатора. Далее конденсатор опять начинает разряжаться через катушку, как и в момент включения t0, но направление тока будет противоположным, так как полярность конденсатора в момент t2 противоположна полярности в момент t0.
После разряда опять происходит заряд, таким образом энергия переходит от C(CU2/2) к L(LI2/2); и от L к С т.е. возникают колебания. Математический анализ показывает, что напряжение и ток в контуре состоящем из L и С изменяются по синусоидальному закону. Промежуток времени от t0 до tn составляет период возникших синусоидальных колебаний. Период и ω зависит от величины С и L. Частота возникающих колебаний называется резонансной частотой контура. В контуре энергия С CU2/2 переходит к L LІ2/2 и наоборот, значит CU2/2 = LI2/2 или CU2 = LI2*, сопротивление катушки по переменному току зависит от частоты: XL = ωL, тогда как в контуре I=U/ωL. Если подставить это в *, то получится CU2 = L(U/ωL)2 → CU2 = LU2/ω2L2 → ω2 = 1/LC → ω = 1 / Из звездочки можно вывести сопротивление контура: CU2 = LI2 → U2/I2 = L/C → U/I = В реальных контурах имеются потери энергии на активных сопротивлениях, поэтому при каждой последующей перезарядке напряжение уменьшается на какую-то величину, зависящую от сопротивления потерь. Колебания затухают по экспоненциальному закону (а не линейно, так как с уменьшением амплитуды уменьшаются и потери). Чем больше потери в контуре (чем больше r), тем быстрее затухают колебания.
Рассмотрим процессы, происходящие в цепи, составленной из конденсатора и катушки индуктивности, в которых не происходит потери энергии. Разомкнув ключ К2, замкнем ключ К1 и зарядим конденсатор от источника постоянного тока. Затем разомкнем ключ К1 и замкнем ключ К2. Конденсатор начнет разряжаться через катушку. Поскольку до этого в катушке индуктивности тока не было, то вследствие действия ЭДС самоиндукции ток iL увеличивается постепенно от нулевого значения, а напряжение на конденсаторе uC уменьшается. При этом запас энергии электрического поля конденсатора уменьшается, а запас энергии магнитного поля катушки увеличивается. Когда напряжение на конденсаторе упадет до нуля, вся энергия электрического поля конденсатора перейдет в энергию магнитного поля катушки, которая достигнет максимума. Одновременно ток, проходящий через катушку, также достигнет максимального значения. Так как ток в катушке не может прекратиться скачком, то он спадает постепенно, сохраняя прежнее направление, и перезаряжает при этом конденсатор, т. е. заряжает его пластины зарядами противоположного знака по сравнению с теми, которые были на них до этого. Когда же ток спадет до нуля, вся энергия магнитного поля катушки перейдет в энергию электрического поля конденсатора и напряжение на конденсаторе станет таким же, каким оно было в начале процесса, но с обратным знаком. Затем процесс повторится, но разряд уже будет проходить в противоположном направлении.
Таким образом, в цепи происходят незатухающие электрические колебания с поочередным переходом энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно. Поэтому цепь, состоящую из конденсатора и катушки, называют колебательным контуром. Так как потерь в идеальном контуре нет, то этот процесс продолжается бесконечно. Аналогичные явления можно наблюдать в механических колебательных системах, например при колебаниях идеального маятника, в котором его потенциальная энергия в верхнем положении переходит в кинетическую энергию при нижнем положении и наоборот. Рассмотренный процесс колебаний в контуре носит название свободных колебаний, так как он протекает без влияния внешней возбуждающей силы только благодаря некоторому запасу энергии в одном из элементов цепи. Ток и напряжение в контуре изменяются по синусоидальному закону, но со сдвигом по фазе на 900. Из равенства максимальных энергий конденсатора U2mcC/2 и катушки І2mcL/2, где Umc — амплитуда напряжения на конденсаторе; I2mL — амплитуда тока в катушке; С — емкость конденсатора и L — индуктивность катушки, следует
Эта величина называется характеристическим сопротивлением контура. Данное отношение амплитуды напряжения на элементах контура к амплитуде протекающего через них тока определяется реактивными сопротивлениями этих элементов. Поскольку на катушке и конденсаторе действуют одинаковые по амплитуде напряжения, и через них протекает одинаковый ток, то их сопротивления равны. Если при свободных колебаниях сопротивления конденсатора и катушки равны, то в контуре может проходить ток только определенной частоты, при которой
где ω0 — круговая частота свободных или, как их называют, собственных колебаний контура. Из этого выражения получаем формулу для определения круговой частоты собственных колебаний контура:
Здесь ω — в радианах в секунду, L — в генри и С — в фарадах. Тогда характеристическое сопротивление контура можно записать в виде
Частота собственных колебаний (в герцах) контура может быть найдена по формуле
а период колебаний в контуре
Увеличение периода колебаний с увеличением индуктивности и емкости контура объясняется тем, что чем больше индуктивность контура, тем медленнее происходит изменение тока, и чем больше емкость, тем больше времени требуется на перезарядку конденсатора.
|
||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1127; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.38.184 (0.009 с.) |


 ).
).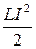 ).
). ─ резонанс частоты контура.
─ резонанс частоты контура.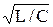 = Z – волновое сопротивление контура.
= Z – волновое сопротивление контура.