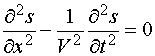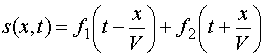Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонические колебания и их характеристики: амплитуда, фаза, период и частота. Метод векторных диаграмм как способ представления гармонических колебаний.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
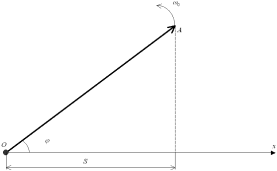
Гармонические колебания и их характеристики: амплитуда, фаза, период и частота. Метод векторных диаграмм как способ представления гармонических колебаний. Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Простейшим типом колебаний являются гармонические колебания - колебания, при которых колеблющаяся величина изменятся со временем по закону синуса (косинуса). Гармонические колебания величины s описываются уравнением типа s =A cos (ω0 t +φ), (1) где А – максимальное значение колеблющейся величины, называемое амплитудой колебания, ω0 – круговая (циклическая) частота, φ – начальная фаза колебания в момент времени t=0, (ω0 t + φ) – фаза колебания в момент времени t. Фаза колебания определяет значения колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от 1 до -1, то s может принимать значения от +А до -А. Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение равное 2π, т.е. ω0 (t+T)+ φ =(ω0 t + φ)+ 2π, откуда T=2π/ω0 (2) Величина, обратная периоду колебаний, ν=1/T (3) т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (2) и (3), получим ω0 = 2πν Единица частоты - герц (Гц): 1 Гц – частота периодического процесса, при которой за 1 секунду совершается 1 цикл процесса. Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки О, выбранной на оси x под углом φ, равным начальной фазе колебания, откладывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания (см. рисунок 1).
Если этот вектор привести во вращение с угловой скоростью w0, равной циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси x и принимать значения от -А до +А, а колеблющаяся величина будет изменяться со временем по закону s =A cos (ω0 t +φ). Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольной точки оси под углом φ, равным начальной фазе, и вращающегося с угловой скоростью ω0 вокруг этой точки.
Свободные гармонические колебания в колебательном контуре, их частота и период. Фазовые соотношения между колебаниями тока в контуре и напряжением на конденсаторе. Энергия свободных гармонических колебаний в колебательном контуре. Колебательный контур – электрическая цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R (рис. 1).
Возрастающий ток разряда, создавая увеличивающееся магнитное поле, вызывает появление ЭДС самоиндукции (катушка поэтому обладает индуктивным сопротивлением Исходя из этого правила, для контура, содержащего катушку индуктивностью L, конденсатор емкостью С и резистор сопротивлением R, I R + U c = e s , где IR – напряжение на резисторе; U с = q / C – напряжение на конденсаторе;
Разделив уравнение (1) на L и подставив
В данном колебательном контуре внешние ЭДС отсутствуют, поэтому рассматрисаемые колебания представляют собой свободные колебания. Если сопротивление R=0, то свободные электромагнитные колебания в контуре являются гармоническими. Тогда из (2) получим дифференциальное уравнение свободных колебаний заряда q в контуре: Решением этого уравнения является гармоническое колебание заряда по закону q = q m cos (wo t + j), (4) где q m – амплитуда колебаний заряда с циклической частотой wo, называемой собственной частотой контура:
и периодом, определяемым формулой Томсона: T = 2p Напряжение на конденсаторе
где U m = q m/ C – амплитуда напряжения. Продифференцировав функцию (4) по времени, получим выражение для силы тока
где I m = wo q m –амплитуда силы тока. Из сопоставления формул (4), (7) и (8), видно, что в момент, когда ток достигаем максимального значения, заряд и напряжение на конденсаторе обращаются в нуль и наоборот.
Вынужденные колебания в последовательном RLС-контуре под действием синусоидальной электродвижущей силы. Векторная диаграмма напряжений. Полное сопротивление контура переменному току. Амплитуда и фаза вынужденных колебаний. Резонансные кривые. Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями. Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Внешний источник периодического воздействия обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь. Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте ω0. Если частота ω0 свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте ω внешнего источника. Для установления вынужденных стационарных колебаний после включения в цепь внешнего источника необходимо некоторое время Δt. Это время по порядку величины равно времени τ затухания свободных колебаний в цепи. Электрические цепи, в которых происходят установившиеся вынужденные колебания под действием периодического источника тока, называются цепями переменного тока. Рассмотрим последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рис. 2.3.1): e (t) = e0cos ωt, где e0 – амплитуда, ω – круговая частота.
Рисунок 2.3.1.Вынужденные колебания в контуре Предполагается, что для электрической цепи, изображенной на рис. 2.3.1, выполнено условие квазистационарности. Поэтому для мгновенных значений токов и напряжений можно записать закон Ома: Теперь можно построить векторную диаграмму для последовательного RLC-контура, в котором происходят вынужденные колебания на частоте ω. Поскольку ток, протекающий через последовательно соединенные участки цепи, один и тот же, векторную диаграмму удобно строить относительно вектора, изображающего колебания тока в цепи. Амплитуду тока обозначим через I0. Фаза тока принимается равной нулю. Это вполне допустимо, так как физический интерес представляют не абсолютные значения фаз, а относительные фазовые сдвиги. Векторная диаграмма для последовательного RLC-контура изображена на рис. 2.3.2.
Векторная диаграмма на рис. 2.3.2 построена для случая, когда Из рисунка видно, что Из выражения для I0 видно, что амплитуда тока принимает максимальное значение при условии
Явление возрастания амплитуды колебаний тока при совпадении частоты ω колебаний внешнего источника с собственной частотой ω0 электрической цепи называется электрическим резонансом. При резонансе При последовательном резонансе (ω = ω0) амплитуды UC и UL напряжений на конденсаторе и катушке резко возрастают: понятие добротности RLC-контура:
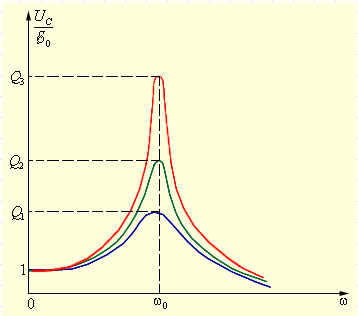
Рисунок 2.3.4. Резонансные кривые для контуров с различными значениями добротности Q. Рис. 2.3.4 иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды UC напряжения на конденсаторе к амплитуде е0 напряжения источника от его частоты ω для различных значений добротности Q. Кривые на рис. 2.3.3 называются резонансными кривыми. Полное сопротивление: Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения. читывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим:
Уравнение плоской волны Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t: Пусть колебание точек, лежащих в плоскости х=0, имеет вид (при начальной фазе ф=0)
Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости х=0, т.е.
Уравнение сферической волны
В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна wt (т.е. ф=0). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу
Волновое уравнение В 1863 г. Максвелл предсказал на основе полученных им уравнений электромагнетизма существование электромагнитных волн. Покажем, что в вакууме векторы поля удовлетворяют волновому уравнению. Напишем систему уравнений Максвелла:
Продифференцировав уравнение (1) по времени и заменив в полученном уравнении Пользуясь формулой векторного анализа
Аналогичным образом, исключая из уравнений (1) и (2), находим, что вектор H удовлетворяет волновому уравнению: где – Общее решение этого уравнения имеет вид: где f1 и f2 – произвольные функции, а аргументы этих функций представляют собой специальные комбинации переменных x,t и постоянной V. Смысл этих решений прост. Если в момент t=0 графически изобразить функции f1(x) и f2(x), то в последующие моменты времени эти функции смещаются вдоль оси X со скоростью V как целое: f1 – вправо, а f2 - влево. - Распространение электромагнитной волны в диэлектрике представляет собой непрерывное поглощение и переизлучение электромагнитной энергии электронами и ионами вещества, совершающими вынужденные колебания в переменном электрическом поле волны. При этом в диэлектрике происходит уменьшение скорости волны.
Гармонические колебания и их характеристики: амплитуда, фаза, период и частота. Метод векторных диаграмм как способ представления гармонических колебаний. Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Простейшим типом колебаний являются гармонические колебания - колебания, при которых колеблющаяся величина изменятся со временем по закону синуса (косинуса). Гармонические колебания величины s описываются уравнением типа s =A cos (ω0 t +φ), (1) где А – максимальное значение колеблющейся величины, называемое амплитудой колебания, ω0 – круговая (циклическая) частота, φ – начальная фаза колебания в момент времени t=0, (ω0 t + φ) – фаза колебания в момент времени t. Фаза колебания определяет значения колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от 1 до -1, то s может принимать значения от +А до -А. Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение равное 2π, т.е. ω0 (t+T)+ φ =(ω0 t + φ)+ 2π, откуда T=2π/ω0 (2) Величина, обратная периоду колебаний, ν=1/T (3) т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (2) и (3), получим ω0 = 2πν Единица частоты - герц (Гц): 1 Гц – частота периодического процесса, при которой за 1 секунду совершается 1 цикл процесса. Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки О, выбранной на оси x под углом φ, равным начальной фазе колебания, откладывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания (см. рисунок 1).
Если этот вектор привести во вращение с угловой скоростью w0, равной циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси x и принимать значения от -А до +А, а колеблющаяся величина будет изменяться со временем по закону s =A cos (ω0 t +φ). Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольной точки оси под углом φ, равным начальной фазе, и вращающегося с угловой скоростью ω0 вокруг этой точки.
Свободные гармонические колебания в колебательном контуре, их частота и период. Фазовые соотношения между колебаниями тока в контуре и напряжением на конденсаторе. Энергия свободных гармонических колебаний в колебательном контуре. Колебательный контур – электрическая цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R (рис. 1).
Возрастающий ток разряда, создавая увеличивающееся магнитное поле, вызывает появление ЭДС самоиндукции (катушка поэтому обладает индуктивным сопротивлением Исходя из этого правила, для контура, содержащего катушку индуктивностью L, конденсатор емкостью С и резистор сопротивлением R, I R + U c = e s , где IR – напряжение на резисторе; U с = q / C – напряжение на конденсаторе;
Разделив уравнение (1) на L и подставив
В данном колебательном контуре внешние ЭДС отсутствуют, поэтому рассматрисаемые колебания представляют собой свободные колебания. Если сопротивление R=0, то свободные электромагнитные колебания в контуре являются гармоническими. Тогда из (2) получим дифференциальное уравнение свободных колебаний заряда q в контуре: Решением этого уравнения является гармоническое колебание заряда по закону q = q m cos (wo t + j), (4) где q m – амплитуда колебаний заряда с циклической частотой wo, называемой собственной частотой контура:
и периодом, определяемым формулой Томсона: T = 2p Напряжение на конденсаторе
где U m = q m/ C – амплитуда напряжения. Продифференцировав функцию (4) по времени, получим выражение для силы тока
где I m = wo q m –амплитуда силы тока. Из сопоставления формул (4), (7) и (8), видно, что в момент, когда ток достигаем максимального значения, заряд и напряжение на конденсаторе обращаются в нуль и наоборот.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.214.244 (0.01 с.) |

 Рассмотрим стадии колебательного процесса в идеализированном контуре, у которого активное сопротивление мало (R =0), а индуктивность L и электроемкость С сосредоточены только в катушке и конденсаторе соответственно (контур с сосредоточенными параметрами). Пусть в какой-либо момент времени конденсатор С оказался заряженным. Обкладки конденсатора получили в начальный момент времени (t =0) заряды ± q m и в этот момент между обкладками возникает электрическое поле, энергия которого
Рассмотрим стадии колебательного процесса в идеализированном контуре, у которого активное сопротивление мало (R =0), а индуктивность L и электроемкость С сосредоточены только в катушке и конденсаторе соответственно (контур с сосредоточенными параметрами). Пусть в какой-либо момент времени конденсатор С оказался заряженным. Обкладки конденсатора получили в начальный момент времени (t =0) заряды ± q m и в этот момент между обкладками возникает электрическое поле, энергия которого 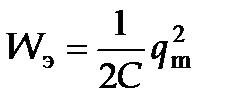 . В следующие моменты времени конденсатор начинает разряжаться и в контуре потечет возрастающий со временем ток I. В результате энергия электрического поля W э будет уменьшаться, а энергия магнитного поля
. В следующие моменты времени конденсатор начинает разряжаться и в контуре потечет возрастающий со временем ток I. В результате энергия электрического поля W э будет уменьшаться, а энергия магнитного поля 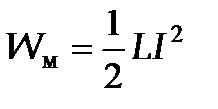 катушки – возрастать. Так как R=0, то на нагревание энергия не расходуется и, согласно закону сохранения энергии, полная энергия
катушки – возрастать. Так как R=0, то на нагревание энергия не расходуется и, согласно закону сохранения энергии, полная энергия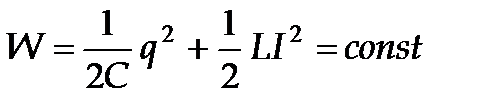 .
.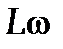 , и конденсатор разряжается не мгновенно). В момент времени, когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля, а, следовательно, и ток достигают максимального значения. Начиная с этого момента, ток в контуре будет убывать, следовательно, начнет ослабевать магнитное поле катушки и в ней индуцируется ток, который течет (по правилу Ленца) в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток. Когда ток прекратится, заряд на обкладках и электрическое поле конденсатора достигнут максимума, а энергия магнитного поля катушки станет равной нулю. Закончится первая половина периода электромагнитных колебаний и конденсатор окажется перезаряженным (поменяются знаки на обкладках). Далее те же процессы начнут протекать в обратном направлении и система, к моменту времени t=T, придет в первоначальное состояние. После этого начнется повторение рассматриваемого цикла разрядки и зарядки конденсатора. Если потерь энергии в контуре нет (R =0), то в контуре совершаются периодические (с периодом Т) и неизменные по амплитуде (незатухающие) колебания заряда q на обкладках конденсатора, напряжения U с на конденсаторе и силы тока I, текущего через катушку индуктивности. Причем, в течение первой половины периода ток идет в одном направлении, а в течение второй половины – в противоположном. Колебания сопровождаются превращениями энергий электрического и магнитного полей.
, и конденсатор разряжается не мгновенно). В момент времени, когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля, а, следовательно, и ток достигают максимального значения. Начиная с этого момента, ток в контуре будет убывать, следовательно, начнет ослабевать магнитное поле катушки и в ней индуцируется ток, который течет (по правилу Ленца) в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток. Когда ток прекратится, заряд на обкладках и электрическое поле конденсатора достигнут максимума, а энергия магнитного поля катушки станет равной нулю. Закончится первая половина периода электромагнитных колебаний и конденсатор окажется перезаряженным (поменяются знаки на обкладках). Далее те же процессы начнут протекать в обратном направлении и система, к моменту времени t=T, придет в первоначальное состояние. После этого начнется повторение рассматриваемого цикла разрядки и зарядки конденсатора. Если потерь энергии в контуре нет (R =0), то в контуре совершаются периодические (с периодом Т) и неизменные по амплитуде (незатухающие) колебания заряда q на обкладках конденсатора, напряжения U с на конденсаторе и силы тока I, текущего через катушку индуктивности. Причем, в течение первой половины периода ток идет в одном направлении, а в течение второй половины – в противоположном. Колебания сопровождаются превращениями энергий электрического и магнитного полей.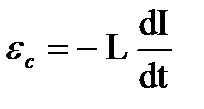 – ЭДС самоиндукции, возникающая в катушке при протекании в ней переменного тока. Следовательно,
– ЭДС самоиндукции, возникающая в катушке при протекании в ней переменного тока. Следовательно,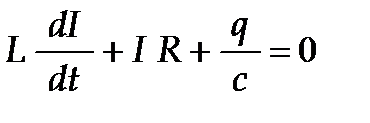 (1) (1)
(1) (1)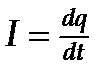 и
и 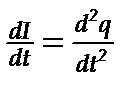 , получим дифференциальное уравнение свободных колебаний заряда q в контуре:
, получим дифференциальное уравнение свободных колебаний заряда q в контуре: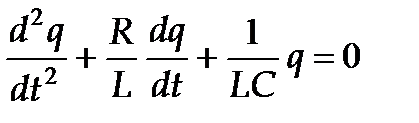 (2)
(2)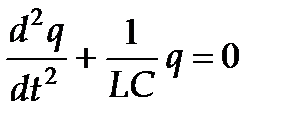 . (3)
. (3)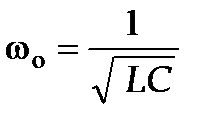 (5) (5)
(5) (5)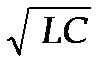 . (6)
. (6)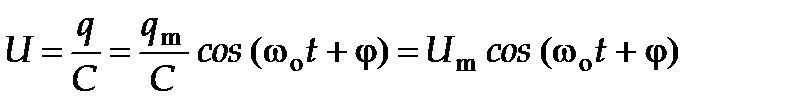 , (7)
, (7)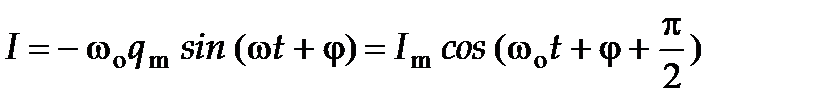 , (8) (8)
, (8) (8)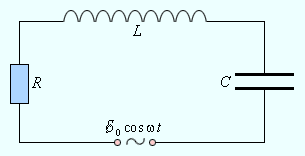 -
-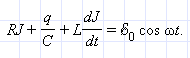 . Величина
. Величина 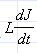 -это ЭДС самоиндукции катушки, перенесенная с изменением знака из правой части уравнения в левую. Эту величину принято называть напряжением на катушке индуктивности. Уравнение вынужденных колебаний можно записать в виде: uR + uC + uL = e (t) = e0 cos ωt, где uR (t), uC (t) и uL (t) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами UR, UC и UL. При установившихся вынужденных колебаниях все напряжения изменяются с частотой ω внешнего источника переменного тока
-это ЭДС самоиндукции катушки, перенесенная с изменением знака из правой части уравнения в левую. Эту величину принято называть напряжением на катушке индуктивности. Уравнение вынужденных колебаний можно записать в виде: uR + uC + uL = e (t) = e0 cos ωt, где uR (t), uC (t) и uL (t) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами UR, UC и UL. При установившихся вынужденных колебаниях все напряжения изменяются с частотой ω внешнего источника переменного тока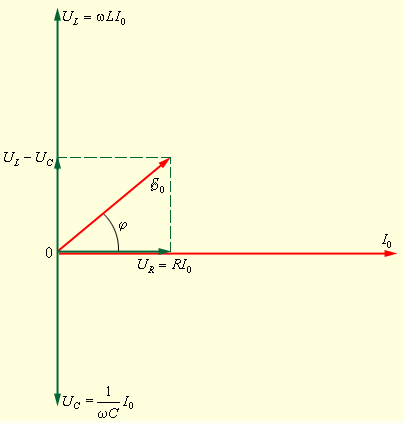 - Рисунок 2.3.3.Векторная диаграмма для последовательной RLC-цепи
- Рисунок 2.3.3.Векторная диаграмма для последовательной RLC-цепи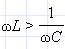 или
или 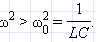 В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.
В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.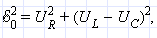 откуда следует
откуда следует 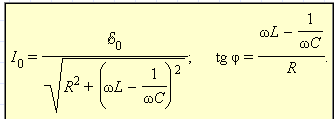
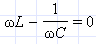 или
или 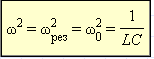
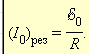 Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).
Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).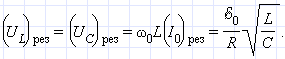
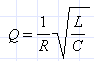
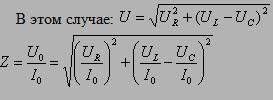
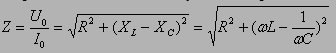 (2)
(2)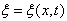
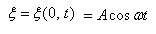 Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время 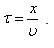 .
.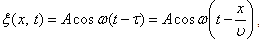 – это уравнение плоской волны.
– это уравнение плоской волны.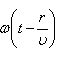 . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону 1/ r. Следовательно, уравнение сферической волны:
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону 1/ r. Следовательно, уравнение сферической волны: 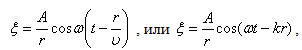
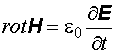 (1)
(1)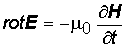 (2)
(2)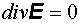 (3)
(3)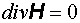 (4)
(4)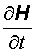 получим:
получим: 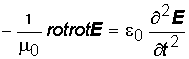 (5)
(5)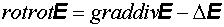 и принимая во внимание уравнение (3), получим:
и принимая во внимание уравнение (3), получим: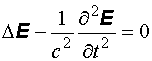 (6)
(6)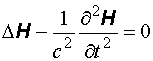 (7)
(7)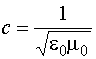 скорость волны. Уравнения (6) и (7) – это волновые уравнения для векторов E и H соответственно. Из того, что векторы E и H удовлетворяют волновому уравнению, вытекает, что электромагнитное поле, которое характеризуют эти векторы, может распространяться в виде волны. Но волны возникают лишь тогда, когда их возбуждают. Электромагнитные волны возбуждаются зарядами и токами. Но, возникнув, электромагнитная волна существует и тогда, когда породивших ее токов и зарядов уже нет. Этим переменное поле отличается от статического, которое не может существовать без порождающих его зарядов. Из уравнений (6) и (7) следует, что электромагнитные волны могут распространяться и в вакууме. Рассмотрим теперь решения волнового уравнения. Начнем с самого простого случая – пространственно одномерного волнового уравнения:
скорость волны. Уравнения (6) и (7) – это волновые уравнения для векторов E и H соответственно. Из того, что векторы E и H удовлетворяют волновому уравнению, вытекает, что электромагнитное поле, которое характеризуют эти векторы, может распространяться в виде волны. Но волны возникают лишь тогда, когда их возбуждают. Электромагнитные волны возбуждаются зарядами и токами. Но, возникнув, электромагнитная волна существует и тогда, когда породивших ее токов и зарядов уже нет. Этим переменное поле отличается от статического, которое не может существовать без порождающих его зарядов. Из уравнений (6) и (7) следует, что электромагнитные волны могут распространяться и в вакууме. Рассмотрим теперь решения волнового уравнения. Начнем с самого простого случая – пространственно одномерного волнового уравнения: