Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волновые процессы и их основные характеристики: длина волны, волновое число, фазовая скорость. Уравнения плоской и сферической волн.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Волной называется процесс распространения колебаний или других возмущений в пространстве. Основными видами волн являются механические упругие волны, волны на поверхности жидкости и электромагнитные волны. Упругими волнами называются волны, которые могут распространяться в упругой среде (т. е. среде, которая сопротивляется сжатию: твердой, жидкой и газообразной). К ним относятся, в частности, ударные, звуковые и сейсмические волны. Упругие волны называют также механическими волнами. Электромагнитные волны могут распространяться как в среде, так и в вакууме (например, радиоволны, световые волны). Характерным свойством волн является перенос энергии без переноса вещества В продольной волне частицы колеблются вдоль направления распространения волны, в поперечной волне колебания частиц совершаются перпендикулярно направлению распространения волны. В жидкой и газообразной среде возможно распространение только продольных волн, в твердой среде - как продольных, так и поперечных. длина́ волны́-расстояние между двумя ближайшими точками гармонической волны, находящимися в одинаковой фазе. Длина волны λ = vT, где Т — период колебаний, v — фазовая скорость волны. ФАЗОВАЯ СКОРОСТЬ -скорость перемещения фазы волны в определ. направлении. В случае монохроматич. плоской волны вида
Волновое число- величина, связанная с длиной волны λ соотношением: k = 2π/λ (число волн на длине 2π). В спектроскопии В. ч. часто называют величину, обратную длине волны (1/λ). Уравнение плоской волны Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t: Пусть колебание точек, лежащих в плоскости х=0, имеет вид (при начальной фазе ф=0)
Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости х=0, т.е.
Уравнение сферической волны
В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна wt (т.е. ф=0). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу
Волновое уравнение для электромагнитного поля. Электромагнитные волны в диэлектриках и их свойства. Волновое уравнение В 1863 г. Максвелл предсказал на основе полученных им уравнений электромагнетизма существование электромагнитных волн. Покажем, что в вакууме векторы поля удовлетворяют волновому уравнению. Напишем систему уравнений Максвелла:
Продифференцировав уравнение (1) по времени и заменив в полученном уравнении Пользуясь формулой векторного анализа
Аналогичным образом, исключая из уравнений (1) и (2), находим, что вектор H удовлетворяет волновому уравнению: где – Общее решение этого уравнения имеет вид: где f1 и f2 – произвольные функции, а аргументы этих функций представляют собой специальные комбинации переменных x,t и постоянной V. Смысл этих решений прост. Если в момент t=0 графически изобразить функции f1(x) и f2(x), то в последующие моменты времени эти функции смещаются вдоль оси X со скоростью V как целое: f1 – вправо, а f2 - влево. - Распространение электромагнитной волны в диэлектрике представляет собой непрерывное поглощение и переизлучение электромагнитной энергии электронами и ионами вещества, совершающими вынужденные колебания в переменном электрическом поле волны. При этом в диэлектрике происходит уменьшение скорости волны.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 760; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.227.250 (0.007 с.) |

 где А - амплитуда, j-фаза, w-круговая частота, k - волновое число, t- время, х - расстояние, отсчитываемое в направлении распространения волны)
где А - амплитуда, j-фаза, w-круговая частота, k - волновое число, t- время, х - расстояние, отсчитываемое в направлении распространения волны)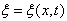
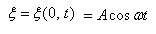 Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время 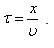 .
.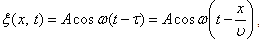 – это уравнение плоской волны.
– это уравнение плоской волны.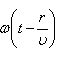 . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону 1/ r. Следовательно, уравнение сферической волны:
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону 1/ r. Следовательно, уравнение сферической волны: 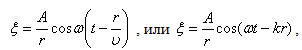
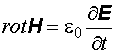 (1)
(1)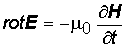 (2)
(2)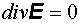 (3)
(3)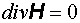 (4)
(4)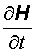 получим:
получим: 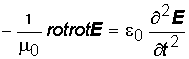 (5)
(5)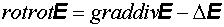 и принимая во внимание уравнение (3), получим:
и принимая во внимание уравнение (3), получим: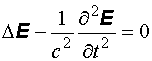 (6)
(6)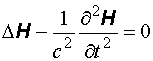 (7)
(7)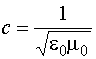 скорость волны. Уравнения (6) и (7) – это волновые уравнения для векторов E и H соответственно. Из того, что векторы E и H удовлетворяют волновому уравнению, вытекает, что электромагнитное поле, которое характеризуют эти векторы, может распространяться в виде волны. Но волны возникают лишь тогда, когда их возбуждают. Электромагнитные волны возбуждаются зарядами и токами. Но, возникнув, электромагнитная волна существует и тогда, когда породивших ее токов и зарядов уже нет. Этим переменное поле отличается от статического, которое не может существовать без порождающих его зарядов. Из уравнений (6) и (7) следует, что электромагнитные волны могут распространяться и в вакууме. Рассмотрим теперь решения волнового уравнения. Начнем с самого простого случая – пространственно одномерного волнового уравнения:
скорость волны. Уравнения (6) и (7) – это волновые уравнения для векторов E и H соответственно. Из того, что векторы E и H удовлетворяют волновому уравнению, вытекает, что электромагнитное поле, которое характеризуют эти векторы, может распространяться в виде волны. Но волны возникают лишь тогда, когда их возбуждают. Электромагнитные волны возбуждаются зарядами и токами. Но, возникнув, электромагнитная волна существует и тогда, когда породивших ее токов и зарядов уже нет. Этим переменное поле отличается от статического, которое не может существовать без порождающих его зарядов. Из уравнений (6) и (7) следует, что электромагнитные волны могут распространяться и в вакууме. Рассмотрим теперь решения волнового уравнения. Начнем с самого простого случая – пространственно одномерного волнового уравнения: